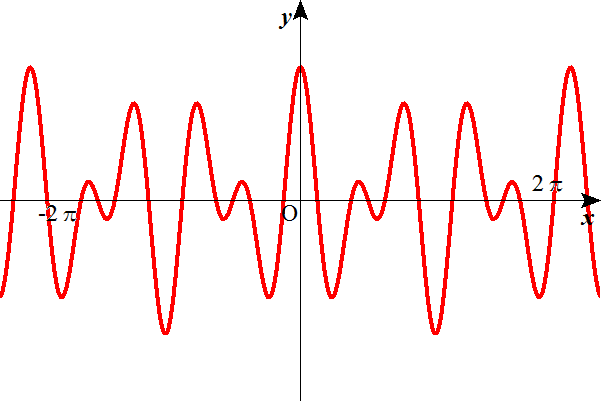
• cosx=k    (-1k1)
  の解は、1周期あたり2つずつある(もちろんk=1や-1のときは｢重解｣だから一つ)。図の●と○。
  y=cosxは｢偶関数｣なので、●と○の関係は、x=0に関して対称、といえる。
  それをはっきりさせるために、図では、1周期をわざと-πから、πにとってある。
  したがって、○をθとすれば、●は(-θ)といえる。
  
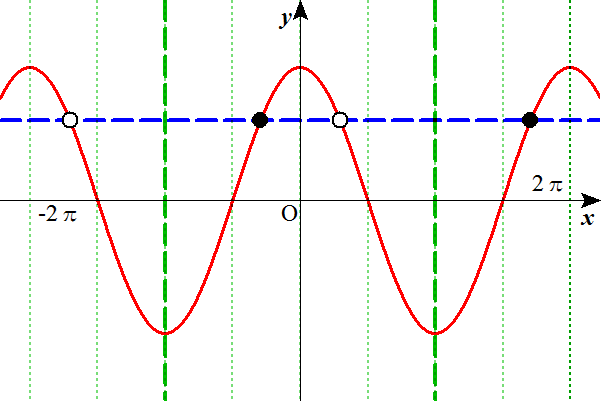
  y=cosxは周期2πの周期関数だから、
  ○すなわちθが解なら、θ+2nπ   (ただし、nは任意の整数)  も解であり、
  ●すなわち(-θ)が解なら、(-θ)+2nπ   (ただし、nは任意の整数)  も解である。
  
  つまり、上の方程式の一般解は、どれか一つの解をθとすれば、
  θ+2nπ   (ただし、nは任意の整数)  
  または、
  -θ+2nπ   (ただし、nは任意の整数)  
• ならば、
  cosα=cosβを満たすα,βの関係は、と言われたら、
  β=α+2nπ   (ただし、nは任意の整数)  
  または、
  β=-α+2nπ   (ただし、nは任意の整数)  
  となる。

  ---

  ということを、私があまり｢好きではない｣(笑)問題集の解説者は、強調したいらしいのだ。
  私としては(笑)、これはあまり｢いけている｣方法ではなく、｢・・・と変形して、解いてもよい｣と書かれている(笑)方法のほうが、好きだ。その理由は後で述べる。
  cosは｢偶関数｣だから、比較的うまくいった。sinではどうだろうか？

  ---

• sinx=k    (-1k1)
  の解は、1周期あたり2つずつある。図の●と○。
  y=sinxは｢奇関数｣なので、cosの場合ほど分かりやすくはないが、●と○の関係は、x=π/2に関して対称、といえる。
  それをはっきりさせるために、図では、1周期をわざと-π/2から、3π/2にとってある。
  したがって、○をθとすれば、●は(π-θ)といえる。
  
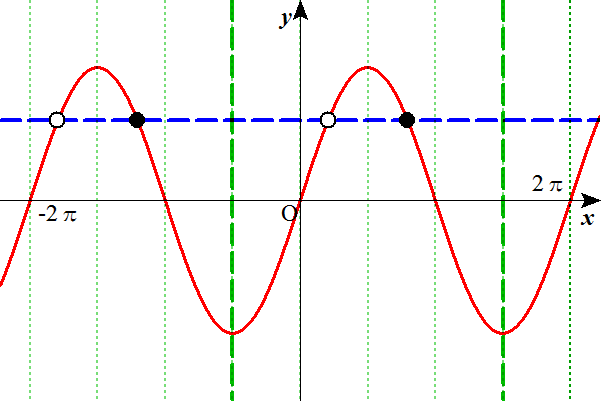
  y=sinxは周期2πの周期関数だから、
  ○すなわちθが解なら、θ+2nπ   (ただし、nは任意の整数)  も解であり、
  ●すなわち(π-θ)が解なら、(π-θ)+2nπ   (ただし、nは任意の整数)  も解である。
  
  つまり、上の方程式の一般解は、どれか一つの解をθとすれば、
  θ+2nπ   (ただし、nは任意の整数)  
  または、
  -θ+(2n+1)π   (ただし、nは任意の整数)  
• ならば、
  sinα=sinβを満たすα,βの関係は、と言われたら、
  β=α+2nπ   (ただし、nは任意の整数)  
  または、
  β=-α+(2n+1)π   (ただし、nは任意の整数)  
  となる。

  ---

  と、なんとかなることはなる。でも、どうしてこんな方法をとるのかなぁ？、という疑問が、私には残る。
  大げさにいうのならば(笑)、これは｢方法論｣上の立場の違い(笑)、なのだが、
  私は、数学の問題を解く際、できるかぎり、なぁ〜んにも頭を使わないで、｢ルール｣に則って｢作業｣を進めていったら、あ、解けていました、というのが一番｢エレガント｣な方法、だと思っている。
  誰にでもできる、という意味で、それは｢民主的｣(！)であるし、
  何度繰り返しても同じ結果がでる、という意味で、それは｢安定｣している！

  ---

• cosα=cosβを満たすα,βの関係は？
  ｢差・積｣の公式、で、
  cosα-cosβ=0
  -2sin{(α+β)/2}sin{(α-β)/2}=0
  sin{(α+β)/2}sin{(α-β)/2}=0
  すなわち、
  sin{(α+β)/2}=0または、sin{(α-β)/2}=0
  
  sinx=0  の一般解は、x=nπ  (ただしnは任意の整数)
  
  であるから、
  (α+β)/2=nπ  (ただしnは任意の整数)
  (α-β)/2=nπ  (ただしnは任意の整数)
  すなわち、
  β=α+2nπ  (ただしnは任意の整数)
  または、
  β=-α+2nπ  (ただしnは任意の整数)
  
  
• sinα=sinβを満たすα,βの関係は？
  ｢差・積｣の公式、で、
  sinα-sinβ=0
  2cos{(α+β)/2}sin{(α-β)/2}=0
  cos{(α+β)/2}sin{(α-β)/2}=0
  すなわち、
  cos{(α+β)/2}=0または、sin{(α-β)/2}=0
  
  cosx=0  の一般解は、x=(2n+1)π/2  (ただしnは任意の整数)
  sinx=0  の一般解は、x=nπ  (ただしnは任意の整数)
  
  であるから、
  (α+β)/2=(2n+1)π/2  (ただしnは任意の整数)
  (α-β)/2=nπ  (ただしnは任意の整数)
  すなわち、
  β=α+2nπ  (ただしnは任意の整数)
  または、
  β=-α+(2n+1)π  (ただしnは任意の整数)
  
  
• ついでに、sinα=cosβを満たすα,βの関係は？、なら？
  sinα-cosβ=0
  どうやら、一般解については、cosのほうが扱いやすいので、sinをcosに変える。もちろん｢余角｣を使って。
  cos(π/2-α)-cosβ=0
  上の結論から、
  β=(π/2-α)+2nπ  (ただしnは任意の整数)
  または、
  β=-(π/2-α)+2nπ  (ただしnは任意の整数)
  
  すなわち、
  β=α+2nπ-π/2  (ただしnは任意の整数)
  または、
  β=-α+2nπ+π/2  (ただしnは任意の整数)

  ---

  もう一つ｢自画自賛｣しておくと、
  A=B
  という型の方程式よりも、
  XY=0
  という型の方程式の方が、すぐれている(！)のは、
  X=0または、Y=0、そのたった二つの場合しかない(！)と、断言できるところにある。
  数学の問題を解く、というのは、・・・が解である、ということを言うことでは、ない。
  ・・・以外に解は、絶対に存在しない、ということを立証することなのでありますから・・・。

  ---

• 話が長くなりまして・・・。
  cos5θ+cos3θ=0、でした。
  私があまり｢好きではない｣(笑)問題集の解説者のとる方法は、
  cos5θ=-cos3θ
  cos5θ=cos(π-3θ)
  上の結論から、
  5θ=(π-3θ)+2nπ  (ただしnは任意の整数)
  または、
  5θ=-(π-3θ)+2nπ  (ただしnは任意の整数)
  すなわち、
  8θ=(2n+1)π  (ただしnは任意の整数)
  または、
  2θ=(2n-1)π  (ただしnは任意の整数)
  もちろん後者は、
  2θ=(2n+1)π  (ただしnは任意の整数)
  でかまわない。
  
  よって、
  θ=(2n+1)π/8  (ただしnは任意の整数)
  または、
  θ=(2n+1)π/2  (ただしnは任意の整数)
  
  
• わたくし的には(笑)、
  cos5θ+cos3θ=0
  2cos4θcosθ=0
  cos4θcosθ=0
  すなわち、
  cos4θ=0または、cosθ=0
  
  4θ=(2n+1)π/2  (ただしnは任意の整数)
  または、
  θ=(2n+1)π/2  (ただしnは任意の整数)
  
  よって、
  θ=(2n+1)π/8  (ただしnは任意の整数)
  または、
  θ=(2n+1)π/2  (ただしnは任意の整数)
  
  
• y=cos5xと、y=-cos3xのグラフ、重ねて描いてみました。
  π/8ごとに縦に点線引いてあります。二つのグラフの交点が、上の解になっていることが分かるでしょう？
  
  
  
• ついでに、y=cos5x+cos3xのグラフ。
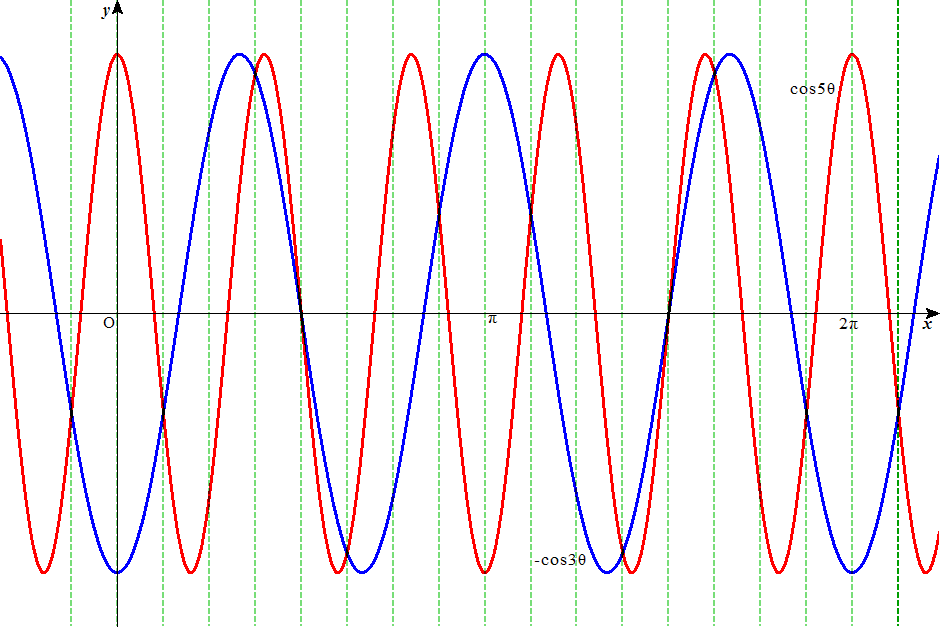
  物理学における｢重ね合わせの原理｣の好例で、二つの波長の異なる正弦波(純音)が重なって、こんな新たな波(音)が発生するのです。
  波長の比が3:5という、結構小さな整数比ですから、かなり｢調和的｣な和音になっているはずです。