• Mg+2H+→Mg2++H2・・・(1)
    • この反応は「不可逆変化」のように、右向きに進行する。
      本当は、「可逆変化」であるか「不可逆変化」であるかは、「閉鎖系」で考えなければならないが、ビーカーの水の中にマグネシウムの塊を放り込むというような普通の実験条件では、「生成物」である気体の水素が「系外」に逃げてしまうから、平衡は次々に右に移動し、ついには、「反応物」であるマグネシウムか、または、水素イオンがなくなるまで、進行し続けることになる。
    • マグネシウムの方は、なくならないよう、十分に大きな塊であったとしよう。
      では、水素イオンは、なくなる、ことがあるのだろうか？「水」の中には、どんなに微量であっても、かならず、水素イオンが存在するではないか？
      「イオン化傾向」がマグネシウムより大きいK,Ca,Naは、いずれも「アルカリ金属」または「アルカリ土類金属」で、水と容易に反応する、といわれる。
      Ca+2H+→Ca2++H2
      の反応がどんどん進行して、水素イオンが消費されると、
      H2O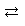H++OH-
      の平衡はどんどん右に移動し、溶液は次第に塩基性になっていく。
      「アルカリ金属」、「アルカリ土類金属」は、水酸化物イオンと沈殿を作らないから、この反応には歯止めがなく、水素イオン濃度が極端に小さくなるまで続くだろう。だから、反応後の水溶液は強塩基性を示す。
    • ところが、2族元素でありながら「アルカリ土類金属」には含まれないマグネシウムは、
      Mg2++OH-→Mg(OH)2
      水酸化マグネシウムという難溶性の塩を作ってしまうから、これがマグネシウムの塊の表面を覆い、それ以上の反応を妨げてしまうだろう。
    • だから、(1)の反応は、ほぼ、酸性領域でしか起こらない、酸の放出した水素イオンがほぼ消費しつくされ、少し塩基性になりかかったところで、止まる、と考えてよいだろう。
  • (1)の反応の「反応速度」について考える。
    Mg+2H+→Mg2++H2・・・(1)
    • マグネシウムの塊が十分大きく、その表面積が十分大きければ、溶液中の水素イオンがそれに一定のエネルギー（活性化エネルギー）以上で衝突すれば、反応は起こる。
      ということは、溶液中の水素イオンの量が大きければ大きいほど、反応が生じる確率は高くなり、したがって、反応速度は大きくなる。
      「比例する」とは限らない。比例するとすれば、
      dC/dt=-kC
      という微分方程式が成り立つことになって、
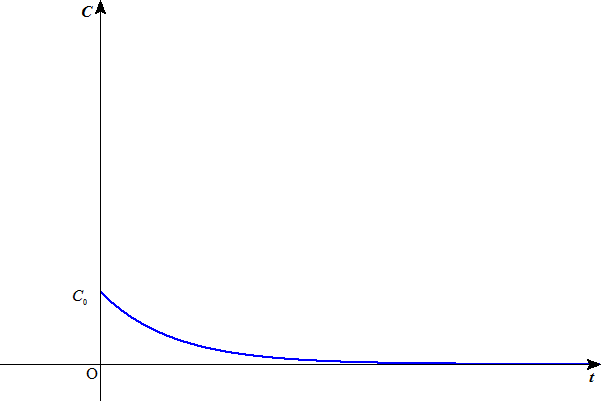
      C=C0e-kt
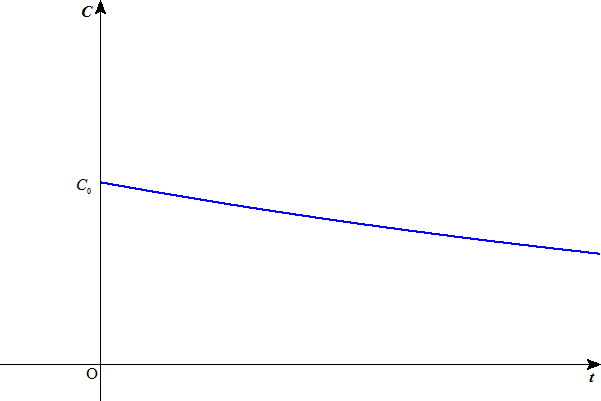
      水素イオン濃度Cは、底が1より小さい指数関数のように減少するだろう。したがって、気体の水素の発生量も、同じようなカーヴを描くだろう。
      (これは、｢1次反応｣を仮定していることになるが、もちろん反応の次数は、実験によって定めるしかないから、はっきりしたことはわからない。でも、大体同じような減少曲線を描くであろうことは、想像できる。)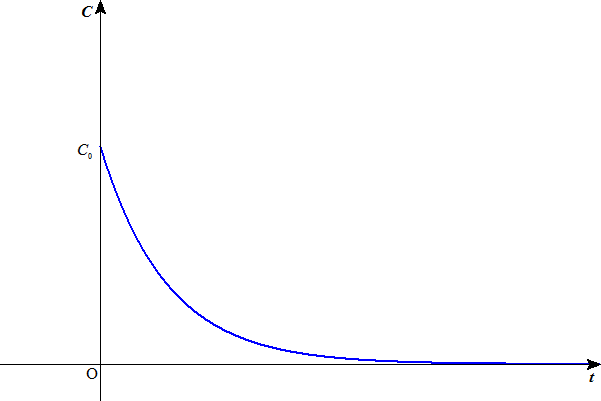

  • 今度は、水素イオンを供給する側、すなわち、酸の方の事情について考える。
    HCl→H++Cl-・・・(2)
    CH3COOH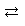H++CH3COO-・・・(3)
    • 塩酸は強酸であるから、どんな濃度条件でもほぼ電離度1と考えられる。だから、塩酸の水溶液中には、HCl分子はほとんど存在せず、(1)によって水素イオンが消費されたとしても、(2)の平衡はすでに限界まで右に偏っているから、もはや、新たに水素イオンを供給することが出来ない。
      つまりこの溶液中には、一定の限りある水素イオンしか存在せず、(1)の反応が進行するに応じて、ただそれが、減少するだけなのである。だから、上のグラフにかなり近いものになるだろう。
    • ところが、酢酸は弱酸であるから、電離度が小さく、反応の初期の水素イオン濃度は、塩酸の場合に比べてはるかに小さいが、(1)の反応の進行に伴って水素イオンが消費されると、(3)の平衡が次々に右に移動して、水素イオンを供給してくれる。
      なくなれば補充してくれる、のであるから、減少の度合い、つまりグラフの傾きの絶対値は、小さい。その様子は下の図のようになるだろう。
    • 塩酸と酢酸の濃度が同じ場合、どちらも1価の酸なのだから、潜在的にもっている水素イオンの物質量は同じである。だから、反応終結までに、(酸が供給した水素イオンがほぼ使い尽くされ、中性になるときまでに)、消費される水素イオンの量は、同じはずである。だから、グラフの曲線下の面積は等しくなるだろう。
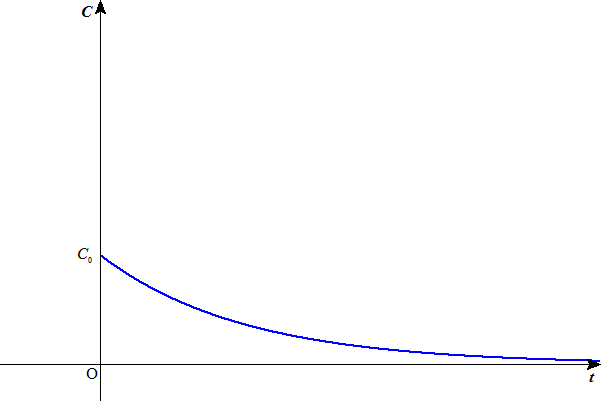
      塩酸の場合酢酸の場合
    • つまり、両者同じ濃度のもとでは、
      • 塩酸のほうが酢酸より最初の反応の勢いはいいが、急速に終わる。
      • 酢酸では塩酸より最初の反応の勢いは小さいが、反応が長続きする。
      • 最終的に消費される水素イオンの量、したがって、
        • 発生する気体の水素の量も、
        • 消費されるマグネシウムの量も、
        同じはずである。
    • 両者の水素イオン濃度が同じになるように調整したとしたら、どうなるか？
      酢酸の電離度は小さいから、反応の初期の水素イオン濃度(グラフ中のC0)を同じにそろえるには、酢酸の濃度を塩酸よりはるかに大きくしなければならない。
      電離度を10-2と概算しても、100倍の濃度が必要である。濃度が大きくなれば、電離度はますます小さくなることも考慮しなければならない。
      こうして酢酸の濃度が著しく大きくなれば、潜在的に供給できる、つまり、(1)によって水素イオンが消費されるごとに(3)の平衡が右に移動して最終的に供給することの出来る水素イオンの量は、電離度が1である塩酸の場合より、はるかに大きくなるだろう。
      だから、グラフは下のようになるだろう。つまり、
      • 最初の反応の勢いは、C0が同じなのだから、両者で同じである。
      • 塩酸では急速に減衰するのに反して、酢酸では、次々に水素イオンが供給されるから、反応は長続きする。
      • 最終的に消費される水素イオンの量、したがって、
        • 発生する気体の水素の量も、
        • 消費されるマグネシウムの量も、
        これらは、グラフ下の面積で比較できるから、酢酸のほうがはるかに大きいことになる。
        塩酸の場合酢酸の場合
  • 具体的に、計算してみよう
    酢酸の初期濃度を c mol/L 、電離度を α とする。溶液1Lについて、
    CH3COOHH++CH3COO-
    はじめc
    電離cαcαcα
    平衡後c(1-α)cαcα
    電離平衡定数  Ka  は、
            Ka= [H+][CH3COO-]  =  (cα)(cα)  =  cα2
    [CH3COOH] c(1-α) 1-α
    • この式は、αについての２次方程式
      cα2 + Kaα - Ka = 0
      であり、これを解けば、
         ・・・(i)
      と、電離度を計算することができるが、
    • ここで、αが充分に１より小さい場合、1-α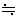1 として
               ・・・(ii)
      という近似式を用いることができる。
    • いま、摂氏25度における酢酸の電離平衡定数Ka=3.00×10-5として、水素イオン濃度が、[H+]=5.00×10-3mol/Lであるような、塩酸、酢酸の、それぞれの濃度を算出する。
      • 塩酸では、電離度1であるから、そのまま5.00×10-3mol/L
      • 酢酸では、
        • 上の(i)式を正直に採用すると、
          α=3.00×10-5÷(5.00×10-3+3.00×10-5)
          二桁以上小さいものは無視してよいとすると、
          α=3.00×10-5÷5.00×10-3
          となって、
        • 結局、上の(ii)式を採用するのと、同じになる。
          α=3.00×10-5÷5.00×10-3=0.6×10-2=6.0×10-3
        c=[H+]/α=5.00×10-3÷6.0×10-3=5/6=0.83mol/L
      • 酢酸はかなりすごい濃度で、塩酸の(1/6)×103倍、167倍くらいの濃度になる。
    ちなみに、電離平衡定数と電離度の関係について、(i)式と(ii)の近似式の比較をしてみた。

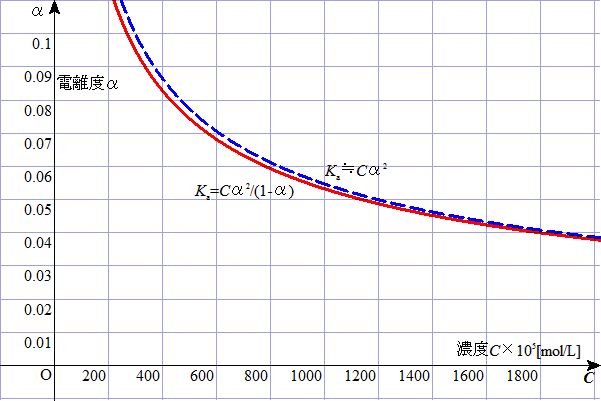
    電離度が0.1より小さく、したがって、濃度が大体3×10-3mol/Lより大きいエリアでは、ほぼ近似式を用いてよいことがわかる。
    • もしこのままの濃度酢酸と塩酸を比較するなら、
      • 最初の反応の勢いは、C0が同じなのだから、両者で同じである。
      • 塩酸では急速に減衰するのに反して、酢酸では、次々に水素イオンが供給されるから、反応は長続きする。
      • 最終的に消費される水素イオンの量、したがって、
        • 発生する気体の水素の量も、
        • 消費されるマグネシウムの量も、
        これらは、グラフ下の面積で比較できるから、酢酸のほうがはるかに大きい、167倍も(！)ことになる。
        塩酸の場合酢酸の場合
    • これらをそれぞれ10倍に希釈する、というのであるから、
      • 塩酸5.0×10-4mol/L
      • 酢酸0.83×10-1=8.3×10-2mol/L
    • この酢酸の電離度は、近似式(ii)が成立すると仮定して、計算すると、

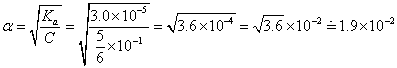
      (こうして1より十分小さい値になったから、近似式でもよかった、ことがわかる。)
      つまり、10倍に薄めることで、電離度は、
      1.9×10-2÷6.0-3で、ほぼ、3倍に増えることがわかった。
    • したがってこのときの両者の水素イオンの濃度[H+]の初期値C0は、
      • 塩酸[H+]=5.0×10-4mol/L
      • 酢酸[H+]=cα=0.83×10-1×1.9×10-2=1.6×10-3mol/L
      酢酸の方が、これまた、1.6×10-3÷5.0×10-4で約3倍大きい。
    • この状態でマグネシウムを投入すると、
      • 最初の反応の勢いは、C0が3倍なのだから、酢酸のほうが勢いがよい。
      • さらに、塩酸では急速に減衰するのに反して、酢酸では、次々に水素イオンが供給されるから、反応は長続きする。
      • 最終的に消費される水素イオンの量、したがって、
        • 発生する気体の水素の量も、
        • 消費されるマグネシウムの量も、
        これらは、グラフ下の面積で比較できるから、酢酸のほうがはるかに大きい、これまた167倍も(！)ことになる。
        塩酸の場合酢酸の場合
  • 最後に、問題の前半にあった、電離度0.043というのは、どのくらいの濃度なんだろうか？
    αが1より十分小さいといえる、として、近似式(ii)から、
    c=3.0×10-5÷(0.043)2=(3.0×10-5)÷{(4.3)2×10-4}=0.16×10-1=1.6×10-2mol/L
    上に掲げたグラフからも、大体同じような値として読み取られるだろう。
    この同じ濃度で、塩酸と酢酸を比較したら、繰り返しになるが、
    • 塩酸のほうが酢酸より最初の反応の勢いはいいが、急速に終わる。
    • 酢酸では塩酸より最初の反応の勢いは小さいが、反応が長続きする。
    • 最終的に消費される水素イオンの量、したがって、
      • 発生する気体の水素の量も、
      • 消費されるマグネシウムの量も、
      同じはずである。
      塩酸の場合酢酸の場合