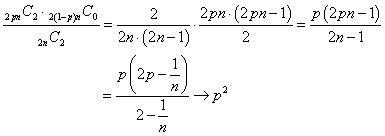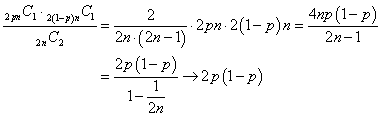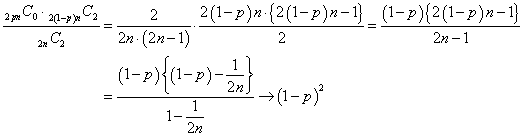(2)(2010追1_5)

(2)(2010追1_5)
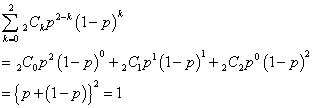
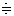 2×6.02×1021
2×6.02×1021
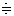 6.02×1023
6.02×1023
| エチレンの種類 | 個数 | 存在比率 |
| 13CH2=13CH2 | 0 | 0% |
| 12CH2=13CH2 | 1 | 2% |
| 12CH2=12CH2 | 49 | 98% |
| エチレンの種類 | 個数 | 存在比率 |
| 13CH2=13CH2 | 1 | 1% |
| 12CH2=13CH2 | 0 | 0% |
| 12CH2=12CH2 | 99 | 99% |
| エチレンの種類 | 個数 | 存在比率 |
| 13CH2=13CH2 | 0 | 0% |
| 12CH2=13CH2 | 2 | 2% |
| 12CH2=12CH2 | 98 | 98% |
| エチレンの種類 | 個数 | 存在比率 |
| 13CH2=13CH2 | 2 | 1% |
| 12CH2=13CH2 | 0 | 0% |
| 12CH2=12CH2 | 198 | 99% |
| エチレンの種類 | 個数 | 存在比率 |
| 13CH2=13CH2 | 1 | 0.5% |
| 12CH2=13CH2 | 2 | 1% |
| 12CH2=12CH2 | 197 | 98.5% |
| エチレンの種類 | 個数 | 存在比率 |
| 13CH2=13CH2 | 0 | 0% |
| 12CH2=13CH2 | 4 | 2% |
| 12CH2=12CH2 | 196 | 98% |
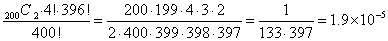
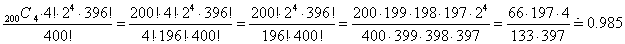
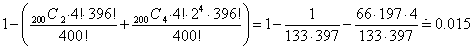
| エチレンの種類 | 個数 | 存在比率 | n→∞とすると | |||
| 13CH2=13CH2 | m |
| 0 | |||
| 12CH2=13CH2 | 2(np-m) |
| 2p | |||
| 12CH2=12CH2 | n(1-2p)+m |
| 1-2p |
|