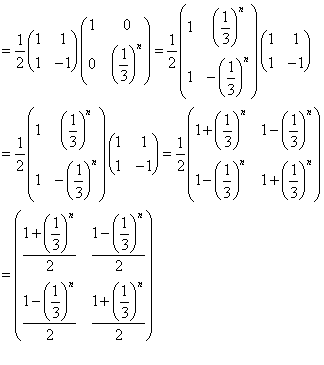an+2+pan+1+qan=0・・・(1)
an+2-αan+1=β(an+1-αan)・・・(2)
と変形できるとして、(1),(2)を比較すると、
an+2-(α+β)an+1+αβan=0・・・(2')
α+β=-p , αβ=qとなり、
α,βはtに関する2次方程式
t2+pt+q=0・・・(3)
の解であることがわかる。
これは、(1)の係数の並び方をそのまま写し取った形をしており、「特性方程式」と呼ばれる。
さて、(2)で bn=an+1-αan と置き換えると、
bn+1=βbn , b1=a2-αa1
これは公比βの等比数列であるから、
bn=b1βn-1
すなわち、
an+1-αan=(a2-αa1)βn-1・・・(4)
ここで、α,βの値、すなわち、「特性方程式」(3)の解のあり方によって、この後の処理手順が若干変わってくる。
|
- 「特性方程式」(3)が2つの異なる実数解をもち、かつ、その一方が1であるとき
αを1と見れば、(4)はすでに「階差型」になっている!
βを1と見れば、(4)はすでに「等比型」になっている!
というわけで、どちらの方法でも、解ける! - 「特性方程式」(3)が2つの異なる解(実数解でなくても、差し支えない!)をもつとき
ここまでの議論で、明らかに、αとβは「入れ替え可能」であるから、(4)が成立するなら、かならず、(4')も成立する。
an+1-αan=(a2-αa1)βn-1・・・(4)
an+1-βan=(a2-βa1)αn-1・・・(4')
両式の辺々を引き算して、an+1を消去すると、
(β-α)an=(a2-αa1)βn-1-(a2-βa1)αn-1
従って、β-α=0でない限り、すなわち「特性方程式」(3)が重解でない限り、この方法で、解ける!・・・(*) - (4)または(4')を、単独で、直接、解く方法はないだろうか?
(4')についても全く同様だから、ここでは(4)について考える。- (4)で、もし、βn-1の部分が「定数」なら、「等比型」に帰着する。もちろん実際にはβは1ではないから、「定数」ではない。
そこで、両辺をβn+1で割ってはどうか?、という「思いつき」が、浮かぶ。
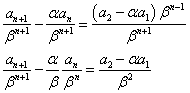
となって、cn=an/βnと置き換えれば、「等比型」になっているではないか! - (4)で、もし、αが1なら、「階差型」に帰着する。もちろん実際にはαは1ではないから、消しゴムで消す、わけにはいかない。
そこで、両辺をαn+1で割ってはどうか?、という「思いつき」が、浮かぶ。
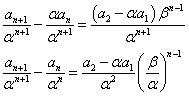
となって、dn=an/αnと置き換えれば、「階差型」になっているではないか!
- (4)で、もし、βn-1の部分が「定数」なら、「等比型」に帰着する。もちろん実際にはβは1ではないから、「定数」ではない。
- 「特性方程式」(3)が重解を持つとき
このときは(*)の方法は使えない。しかし、単独で、解ける。むしろ、もっと簡単だ。
重解をt=γとすると、(4)は、
an+1-γan=(a2-γa1)γn-1・・・(4'')- (4'')で、もし、γn-1の部分が「定数」なら、「等比型」に帰着する。もちろん実際にはγは1ではないから、「定数」ではない。
そこで、両辺をγn+1で割ってはどうか?、という「思いつき」が、浮かぶ。 - (4'')で、もし、γが1なら、「階差型」に帰着する。もちろん実際にはγは1ではないから、消しゴムで消す、わけにはいかない。
そこで、両辺をγn+1で割ってはどうか?、という「思いつき」が、浮かぶ。
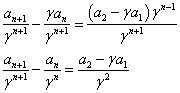
となって、en=an/γnと置き換えれば、- 公比にあたる部分が1であるような「等比型」、かつ、
- 階差数列が、nの関数でなく定数であるような「階差型」、
- (4'')で、もし、γn-1の部分が「定数」なら、「等比型」に帰着する。もちろん実際にはγは1ではないから、「定数」ではない。
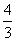 an+1+
an+1+ an=0 a1=
an=0 a1= , a2=
, a2=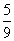
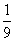 (
(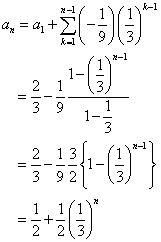

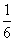 (
( an=0・・・(1)
an=0・・・(1)
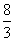 =-
=-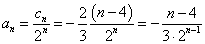
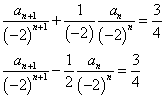
 a1=4
a1=4
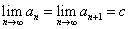 と仮定すると、
と仮定すると、
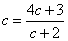
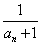 型の変形を考える
型の変形を考える
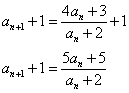
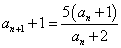 ・・・(1)
・・・(1)
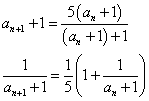
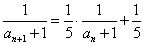 ・・・(2)
・・・(2)
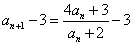
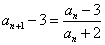 ・・・(3)
・・・(3)
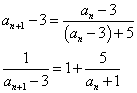
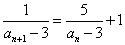 ・・・(4)
・・・(4)
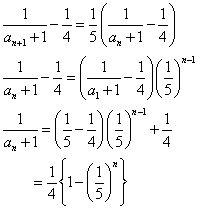
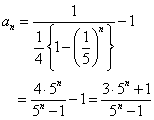
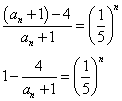
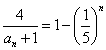
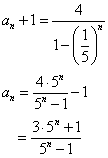
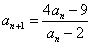 a1=7
a1=7
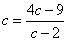
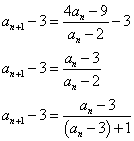
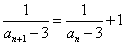
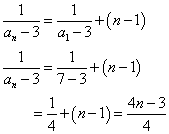
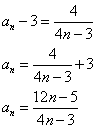
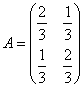
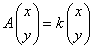 をみたす定数kは2個存在する。これらを求めよ。
をみたす定数kは2個存在する。これらを求めよ。
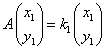 ,
, 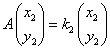
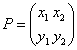 ,
, 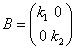 とするとき、AP=PBを示せ。
とするとき、AP=PBを示せ。
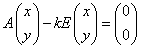
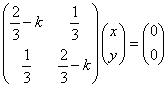
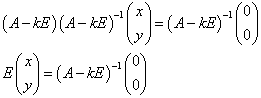
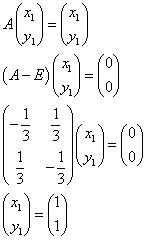
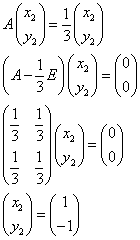
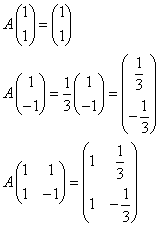
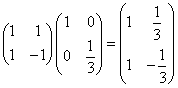
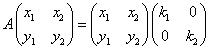
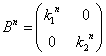 と推定される。
と推定される。