三角関数の周期性、sinの奇関数性、cosの偶関数性、から、次のようなことが言える。

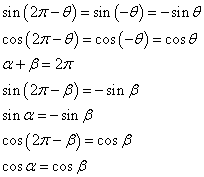
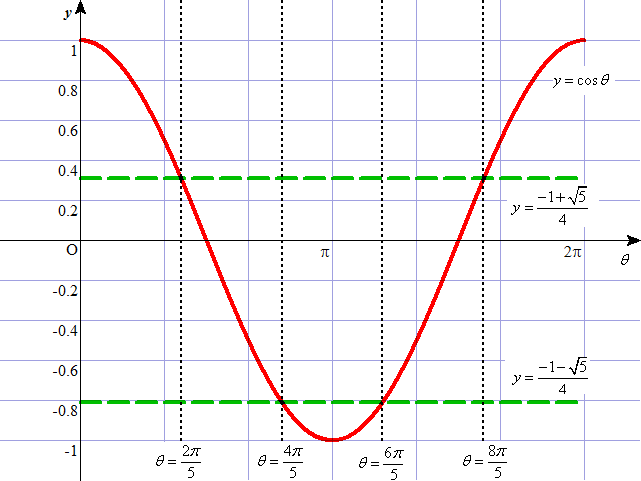
ここで、たとえば円周を五等分した扇型の中心角をαとしてみよう。

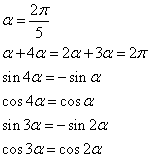
このように、4個の等式が得られる。順次、解いてみると、

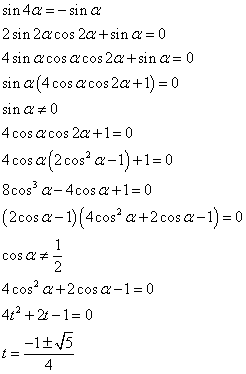
cosαを解とする2次方程式が得られ、その解は上のようになる。
ところで、αの2倍の角をα'としてみると、cosα'もまた、上の2次方程式の解であると言えるから、


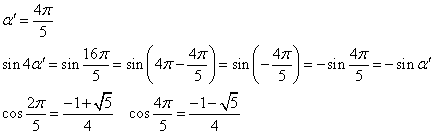
他の3式についても、多少の難易の差はあるものの、いずれも同じ2次方程式に帰着する。



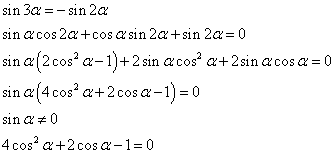
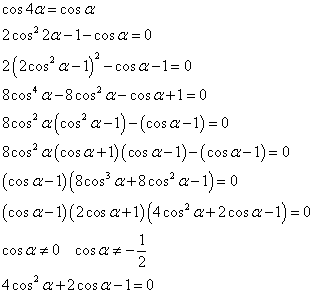
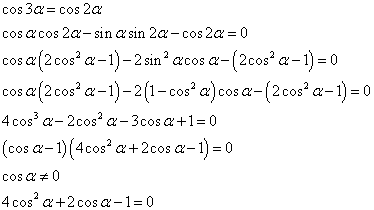
では、円周を7等分した扇型の中心角、ならどうだろう？

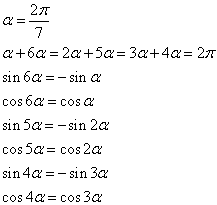
このように6個の等式が得られる。上の二つは6次式、中の二つは5次式、下の二つは4次式となると思われるから、比較的簡単そうな、4次式から解いてみる。

こうしてcosαを解とする3次方程式が得られた。

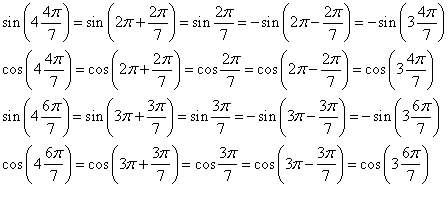
であるからcos2α,cos3αも上の3次方程式の解である。
他の等式についてもほぼ同様であろうから、一つだけ、解いてみる。