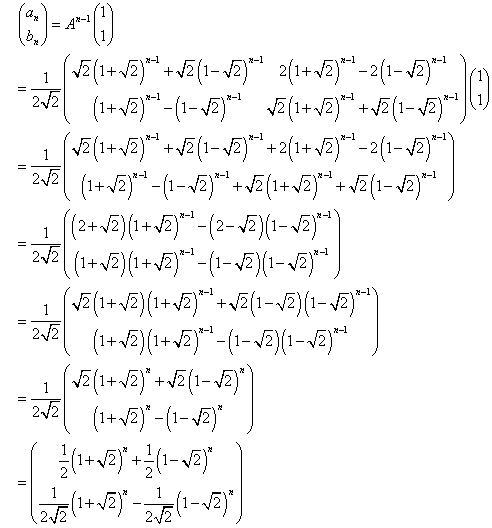• 与えられた連立漸化式は、
  • a_n+1=a_n+2b_n    a₁=1
  • b_n+1=a_n+b_n    b₁=1
  
  行列を用いてかくと、
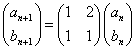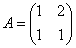          ここで、        とおくと、
  
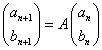
  したがって、一般項a_n,b_nは、
      
• 「固有値」、すなわち、次の式をみたす定数kを求める。
      
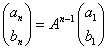
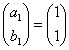
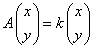
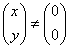
  移項して、
  

  ---

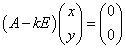
  一般に、
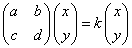      とすると、
  

  ---

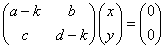
  ここでは、
  
  

  ---

• 「連立1次斉次方程式」の「非自明解」問題
  
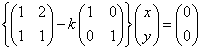
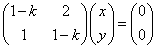
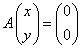
  において、(x,y)=(0,0)がこれをみたすのは当然であるから（これを「自明解」という）これ以外の解（「非自明解」）をもつ条件について考える。すなわち、
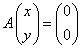      ただし 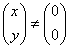   ・・・(2)
  命題『Aが逆行列A^-1をもたなければ、(2)は非自明解をもつ』を、背理法によって証明する。
  (2)が成立し、かつ、Aの逆行列A^-1が存在する、と仮定する。
  両辺に左からこれをかけると、
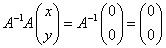      となり 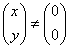       に反する(証明終わり)

  ---

• ｢固有値｣とそれに対応する｢固有ベクトル｣を計算する
  (A-kE)^-1が存在しない    

  ---

  すなわち
  (a-k)(d-k)-bc=0
  k²-(a+d)k-(ad-bc)=0    
  これを「固有方程式」と呼ぶ。
  「ハミルトン・ケーリーの定理」
  A²-(a+d)A-(ad-bc)E=0    
  と係数の並びが同じである。
  ｢固有方程式｣はk(固有値)に関する2次方程式であるから、その解のあり方は3通り、
  1. 2個の異なる実数解
  2. 重解(実数解)
  3. 互いに共役な2個の虚数解
  このうち、
  • I,IIIについては、以下の｢対角化｣によってn乗が計算できる。
  • IIは、独立な｢固有ベクトル｣が1個しか得られないので、この方法では不可能。｢上半三角化｣という別の方法を用いる。

  ---

  ここでは、
  (1-k)(1-k)-2=0・・・(1)
  k²-2k-1=0
  
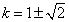
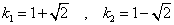      とする（固有値）
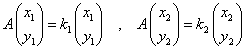      （それぞれの固有値に対応する固有ベクトル）

  ---

                              
          
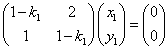
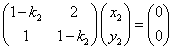
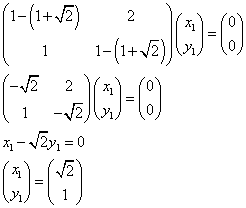
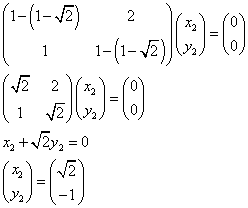
  固有ベクトルは一般に「無数に」存在するから、成分が簡単な形になるそれぞれ一つを選んだ。

  ---

• 2個の｢固有ベクトル｣を列ベクトルとして並べた行列P、｢固有値｣を対角成分としてもつ行列Bに対して、AP=PBを示す
      
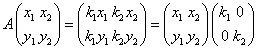
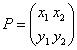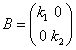    ,      すなわち、
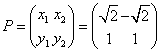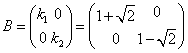    ,      とおくと、
  AP=PB
  「固有方程式」(1)が「重解」でない限り、2つの異なる解（虚数解も含む）に対応する「固有ベクトル」は、「1次独立」のはずである。
  このとき、Pはかならず、逆行列P^-1をもつ。これを両辺に右からかけて、
  APP^-1=PBP^-1
  AE=PBP^-1
  A=PBP^-1
  したがって、
  Aⁿ=(PBP^-1)n=PBP^-1PBP^-1・・・PBP^-1=PBⁿP^-1

  ---

• Bのn乗の推定とその証明
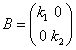      に対して、 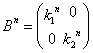       と推定される。・・・(3)
  これを数学的帰納法で証明する。
  1. n=1のとき、        
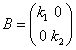
  2. n=mのとき、 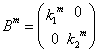       と仮定する
     両辺に右からBをかけて、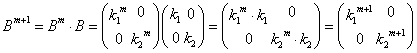
         
     (左からかけた場合も同様)
     n=m+1のときも成立することが示された
  i,iiより、任意の自然数nに対して(3)が成立することが示された

  ---

• Aⁿの計算
  Aⁿ=(PBP^-1)n=PBP^-1PBP^-1・・・PBP^-1=PBⁿP^-1
      
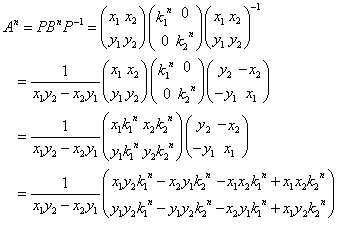
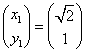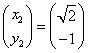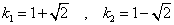    ,    ,      であるから、
      

  ---

  
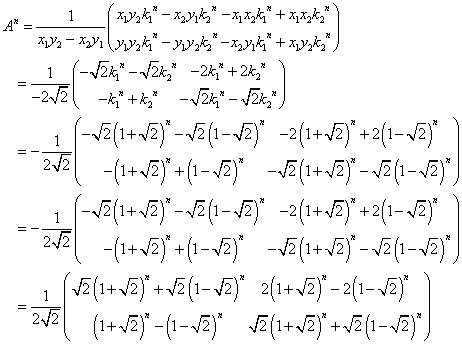
  したがって、
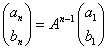      であるから、