- 2か所とも同じ、であれば2点、
- 1か所のみ同じ、であれば1点、
- 2ヶ所とも異なっていれば、0点
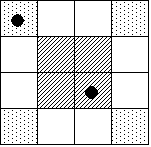
- 以下のようにシートをP,Q,R,Sの4区画に分けると、それぞれの区画の内部の升目は、回転によっても同じ区画にとどまる。
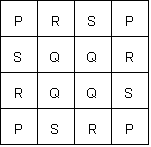
- したがって、A,Bがそれぞれどの区画から2つの升目を選ぶかにより、確率は異なってくるであろう。
その選び方は、以下のように分類できる。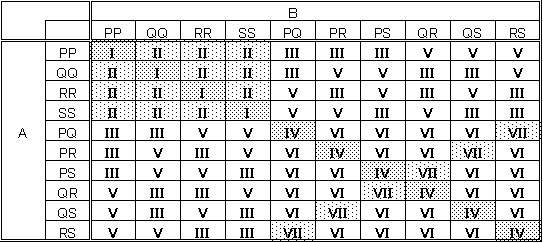
- A,Bともに、同一区画から2ヶ所選び、かつ、A,Bの選んだ区画が同じである場合(PP-PP型)・・・4通り
- A,Bともに、同一区画から2ヶ所選んだが、A,Bの選んだ区画が異なる場合(PP-QQ型)・・・12通り
- A,Bのどちらか一方のみ、同一区画から2ヶ所選び、他方は二つの区画から1ヶ所ずつ選んだ。そのうちの一方が同じ区画である場合(PP-PQ型)・・・24通り
- A,Bともに、異なる二区画から2ヶ所を選び、かつ、A,Bの選んだ区画が二つとも同じである場合(PQ-PQ型)・・・6通り
- A,Bのどちらか一方のみ、同一区画から2ヶ所選び、他方は二つの区画から1ヶ所ずつ選んだ。二人の選んだ区画に重なり合いがない場合(PP-QR型)・・・24通り
- A,Bともに、異なる二区画から2ヶ所を選び、かつ、A,Bの選んだ区画の一方のみ同じである場合(PQ-PR型)・・・24通り
- A,Bともに、異なる二区画から2ヶ所を選び、かつ、二人の選んだ区画に重なり合いがない場合(PQ-RS型)・・・6通り
- 以下、それぞれの場合について検討する。
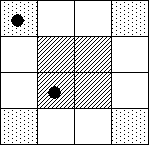
- たとえば、Q区画の場合、A,Bがともに左図のように隣り合わせの升目を選んだならば、これらは回転によって重なるから、得点2となる。
また、A,Bがともに右図のように一つ置きの升目を選んだならば、やはりこれらは回転によって重なるから、得点2となる。
ところが、A,Bのうち一方が左図、他方が右図のように選んだならば、得点は1である。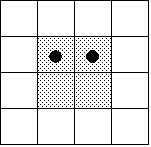
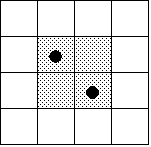
この事情は、他の区画でも変わらない。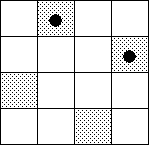
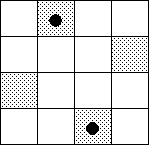
左図「隣り合わせ」型の選び方は4通り、右図「一つ置き」型は2通り。
したがって、得点2となるの場合の数は、4×(4×4+2×2)=80
得点1となるの場合の数は、4×(4×2+2×4)=64 - この場合、回転しても決して重なることがないから、得点は0である。
その場合の数は、12×4C2×4C2=12×6×6=432 - この場合、回転すれば、かならず1か所重なるから、つねに得点は1である。
その場合の数は、24×4C2×(4C1×4C1)=24×6×4×4=2304 - この場合の、すべての場合の数は、6×(4C1×4C1)×(4C1×4C1)=1536
このうち得点2となるのは、例としてPQ型を考えれば、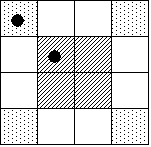
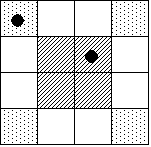
Aが上の4つのいずれかの型(回転して重なるものは、それぞれ4通りある)を選び、Bはそれと同じ型を選べばよいから、
6×(4×4)×4=384
得点1となるのは、その他のすべてであるから、1536-384=1152、
Aが上の4つのいずれかの型を選び、Bはそれと異なる型を選ぶから、
6×(4×4)×(3×4)=1152 - この場合は、すべて得点0である。
その場合の数は、24×4C2×(4C1×4C1)=24×6×4×4=2304 - この場合は、すべて得点1である。
その場合の数は、24×(4C1×4C1)×(4C1×4C1)=6144 - この場合は、すべて得点0である。
その場合の数は、6×(4C1×4C1)×(4C1×4C1)=1536
- たとえば、Q区画の場合、A,Bがともに左図のように隣り合わせの升目を選んだならば、これらは回転によって重なるから、得点2となる。
- 以上、まとめると、
得点2 得点1 得点0 計 I 80 64 0 144 II 0 0 432 432 III 0 2304 0 2304 IV 384 1152 0 1536 V 0 0 2304 2304 VI 0 6144 0 6144 VII 0 0 1536 1536 計 464 9664 4272 14400 - 一方、すべての場合の数は、16C2×16C2=14400であるから、得点ごとの確率は、
得点2 得点1 得点0 計 464/14400
=29/900
=0.03222...9664/14400
=151/225
=0.67111...4272/14400
=89/300
=0.29666...1 - 得点の期待値は、2×(29/900)+1×(151/225)=331/450=0.73555...
|
【問題】A,B二人が次のようなゲームをする。 図のような4×4の升目のシートを一枚ずつ持ち、互いに意思の連絡なく、16個の升目のうち2ヶ所を選ぶ。 二人の選んだ升目が ただし、このシートを、同一平面内で、シートの中央を中心に90度、180度、270度回転して重なるものは、同じ配置とみなすものとする。 | 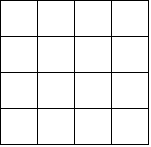 |