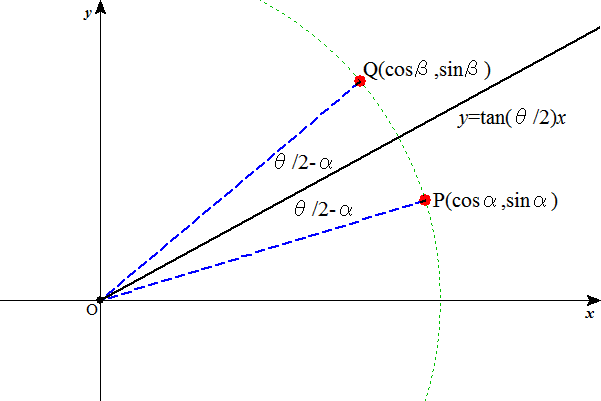
P(x,y),Q(X,Y)に対して、
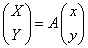 とする。
とする。
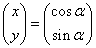 ,
, 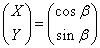 とすると、
とすると、
Aは原点まわりの(θ-2α)回転を表す行列であるから、
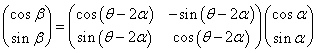
すなわち、
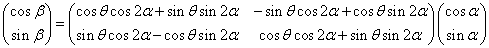
これは次のように、二つの行列の積として表される。
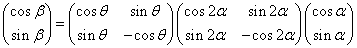
さらに、右側の行列と列ベクトルの積を計算すると、
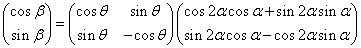
すなわち、
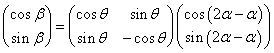
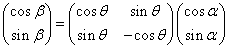
となって、求めるAは、
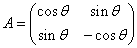
であることがわかった。そうすると、上の式に現れた行列
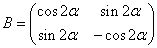
は、直線y=xtanαに関する対称移動を表すことになり、なるほどPはこの直線上の点であるから、この変換によっては移動しない(!)のであった。
だから、原点まわりの(θ-2α)回転は、
- まず、-2α回転し、その後、θ回転しても、(下の図のA→A1→C)
- まず、θ回転し、その後、-2α回転しても、(下の図のA→A2→C)
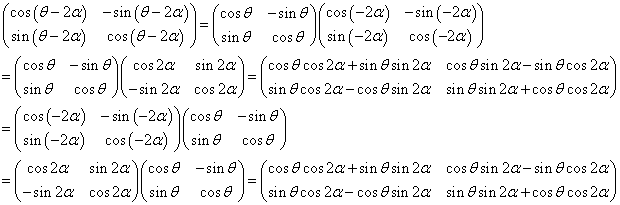
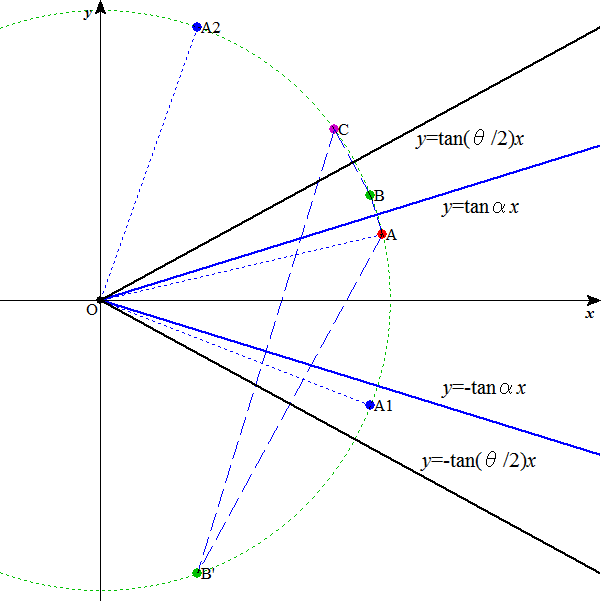
これを、次のようにして、やはりθだけを含む行列と、αだけを含む行列との積に分解すると、
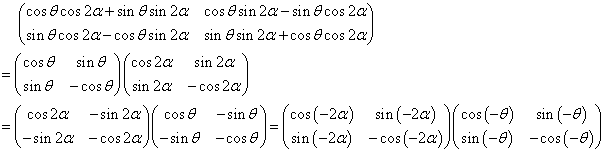
となる。今度は交換可能ではなく、
- まず、y=xtanαに関する対称変換を行い、その後、y=xtan(θ/2)に関する対称変換を行う(下の図のA→B→C)のと、
- まず、y=-xtan(θ/2)に関する対称変換を行い、その後、y=-xtanαに関する対称変換を行う(下の図のA→B'→C)のと、
それにしても、一般に、
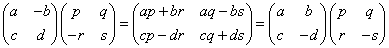
のような変形が出来るのは、なんとも不思議である。
「主対角線」ではない対角成分の一方ずつの符号を変えた行列の積が、「主対角線」成分の一方の符号のみを変えた行列の積に変換できるのだから。
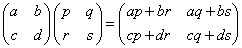
に対して、「主対角線」ではない対角成分の一方ずつに印をつけると、
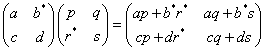
なるほど、「主対角線」成分では印が二重になる。だから、
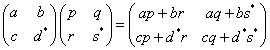
と同じになる。同様に、
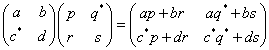
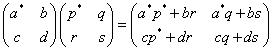
すなわち、
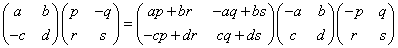
(tA)A=A(tA)=E すなわち、 A-1=tA
となる行列を「直交行列」という。
|A|=|tA| だから、 |(tA)A|=|A(tA)|=|A|2=|tA|2=|E|=1 すなわち、 |A|=1,-1
- 原点まわりのθ回転をあらわす行列、
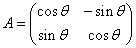 は、|A|=1 の直交行列、
は、|A|=1 の直交行列、
- y=xtan(θ/2)に関する対称変換をあらわす行列、
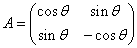 は、|A|=-1 の直交行列、
は、|A|=-1 の直交行列、
- 原点まわりのθ回転をあらわす行列では、
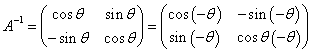
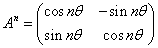
- y=xtan(θ/2)に関する対称変換をあらわす行列では、
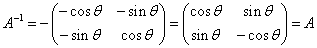
n が奇数のとき、 An=A2m+1=(A2)mA={(tA)A}mA=EmA=A
n が偶数のとき、 An=A2m=(A2)m={(tA)A}m=Em=E
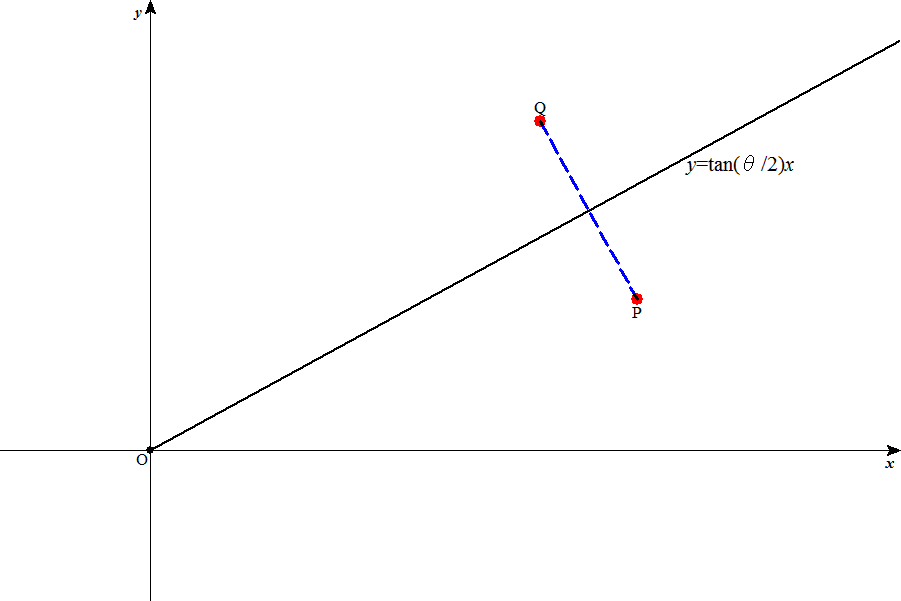
P(x,y),Q(X,Y)に対して、
- 直線PQと、直線y=xtan(θ/2)が直交すること、
- PQの中点Mが、直線y=xtan(θ/2)にあること、
|
|
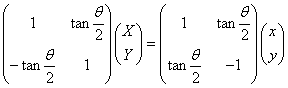
1+tan2(θ/2)は正であるから、
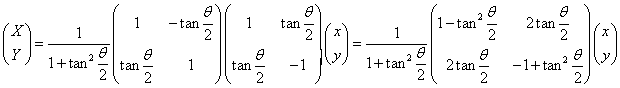
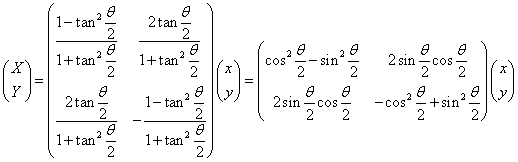
すなわち、
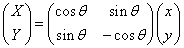
θ=0のとき、
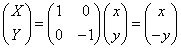 であり、これはx軸に対する対称変換だから、条件を満たしている。
であり、これはx軸に対する対称変換だから、条件を満たしている。
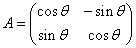
の固有方程式は、t2-2tcosθ+1=0 その解は、
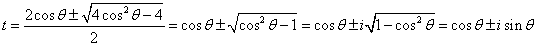
と、複素数で、その絶対値は、1である。固有ベクトルを求めると、
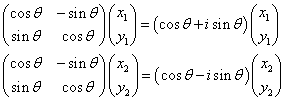
であるから、
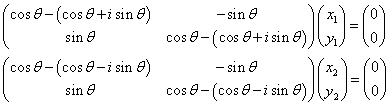
すなわち、
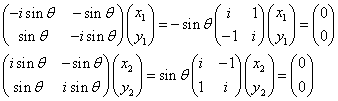
ix1+y1=0 より、 (x1,y1)=(i,1)
ix2-y2=0 より、 (x2,y2)=(1,i)
すなわち、
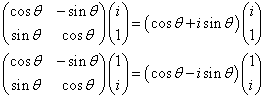
であるから、次のように「対角化」出来る。
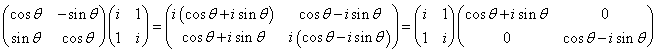
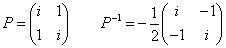
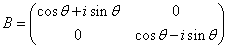 に対して、
に対して、
AP=PB
A=PBP-1
An=PBnP-1
したがって、
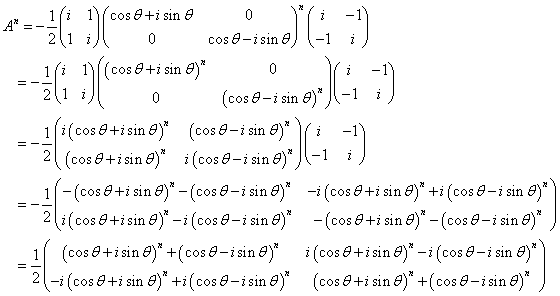
二項定理から、
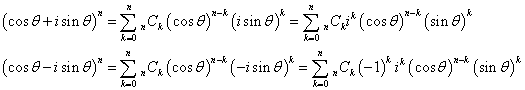
したがって、
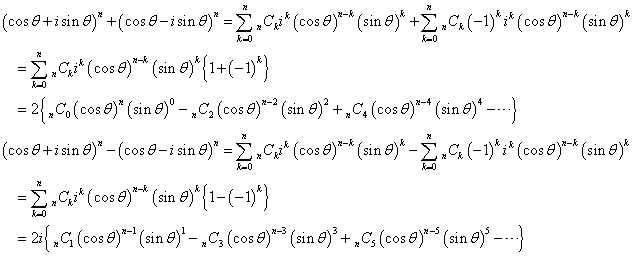
一方、
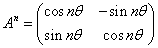 であるから、ここから、
であるから、ここから、
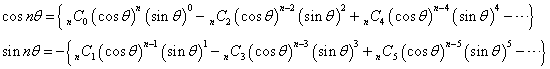
が得られる。
次に、
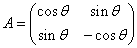
の固有方程式は、t2-1=0 その解は、1,-1
同様に固有ベクトルを求めると、
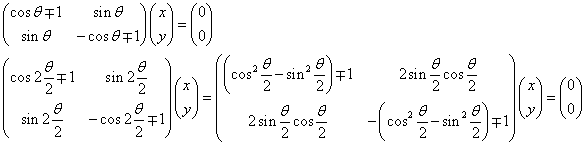
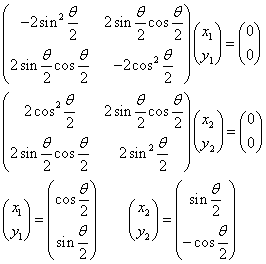
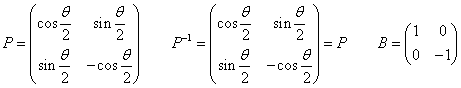 に対して、
に対して、
An=PBnP-1
したがって、
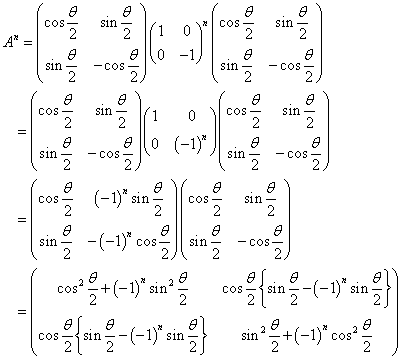
すなわち、nが奇数のとき An=A 、 nが偶数のとき An=E である。
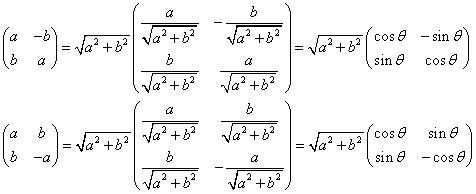
のように変形できるから、それぞれ、
- 原点まわりθ回転と、√(a2+b2)倍拡大、
- 直線y=xtan(θ/2)に関する対称移動と、√(a2+b2)倍拡大、
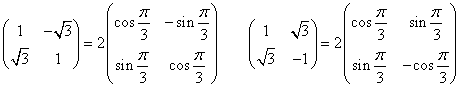
- 左は、原点まわりπ/3回転と、2倍拡大、の合成変換、
- 右は、直線y=xtan(π/6)に関する対称移動と、2倍拡大、の合成変換。
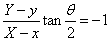 ・・・(i)
・・・(i)
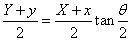 ・・・(ii)
・・・(ii)
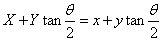 ・・・(i)
・・・(i)
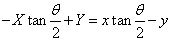 ・・・(ii)
・・・(ii)