• 漸化式
  
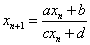
  y_n=x_n-k  と置き換えることで、式を簡略化できないか？、と考えて、
  
  
  
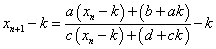
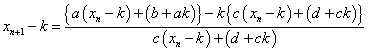
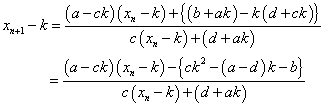
  右辺の分子の定数項(x_nを含まない項)を0にすれば、両辺の逆数を取ることによって、
  a_n+1=pa_n+q    型の漸化式
  に変形できそうである！
  
  これは、xに関する2次方程式
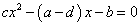    ・・・(1)
  の解、α,βをkとして選べばよいことを意味する。｢解と係数の関係｣より
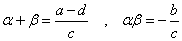    ・・・(2)
  このようなkに対して、両辺の逆数を取ると、
  
  
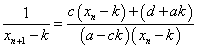
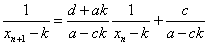
  これは、以下のように置き換えると、
  
  
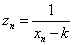
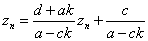
  となっていて、確かに、a_n+1=pa_n+q    型の漸化式であり、解くことが出来る。
  
  
  
  
• 以下、まず、k=α、として計算してみる。αとβは入れ替え可能であるから、k=βの場合も同じ結果が得られることが予想される。、
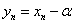    とおくと、
  
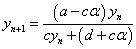
  逆数をとって、
  
  
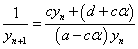
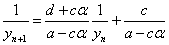
  さらに、 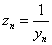   と置き換えると、
  
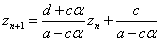
  これは、以下のように、定数γを定めることで、等比数列に変形できる。
  
  
  
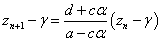
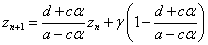
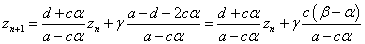
  ここでの変形には、(2)の第1式を用いた。
  
  
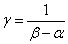
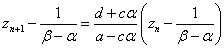
  さらに、 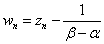   と置き換えて、
  
  
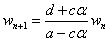
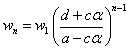
  順次、戻していくと、
  
  
  
  
  
  
  
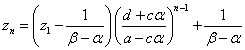
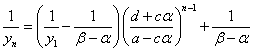
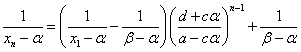
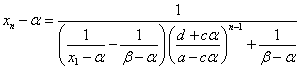
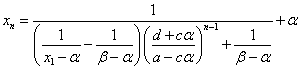
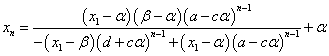
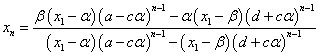
  ここで、ふたたび（2）第1式より、
  
  
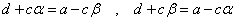
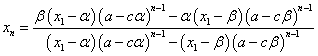
  こうして、一般項が得られた。予想通り、この式は、αとβを入れ替えても、まったく同じ式である。
  
  
  
  
• ところで、2次方程式(1)は、次のように見ることもできる。
  
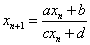
  に対して、分数関数 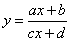   と、  y=x  との交点を与える方程式、
  
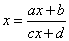
  を考えると、
  
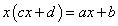
  となり、xについての2次方程式
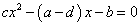    ・・・(1)
  が得られる。こうして｢世間｣では、x_n+1=x_n=x  と｢見た｣式を、この漸化式の｢特性方程式｣と呼んでいるのである。
  
  
  
  
• 次に、(1)の解、α、βを用いて、次式の左辺のような形を作ってみると、
  
  
  
  
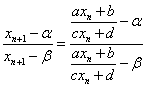
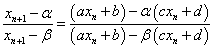
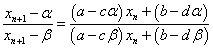
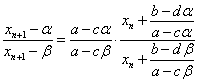
  ここで、(2)より、
  
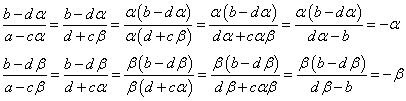
  であるから、
  
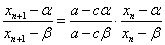
  であるから、となり、これは等比数列であることがわかる。したがって、
  
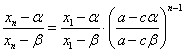
  ここから、x_nを解いて、
  
  
  
  
  
  
  
  
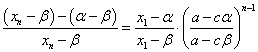
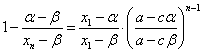
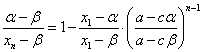
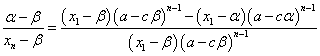
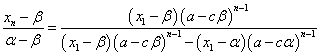
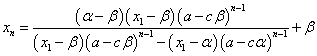
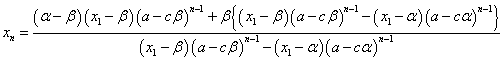
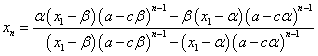
  同じ結果が得られた。
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
• x_nの一般項を、次のようにおく。
  
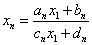
  行列 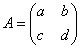   に対して、 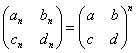   であることを示す。
  1. n=1のとき、
     
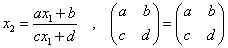
     n=2のとき、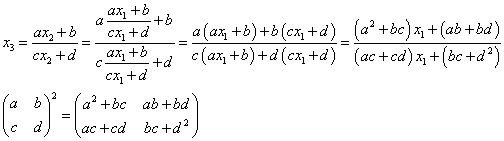
     
  2. n=kに対して、 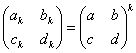   と仮定すると、
     
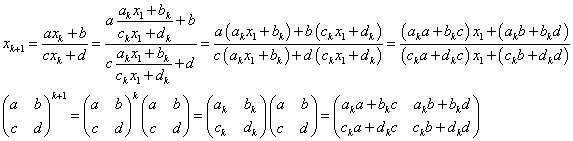
     となり、n=k+1に対しても成り立つ。
     よってi,iiより、任意の自然数nに対して、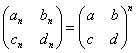    であることが示された。