---

• 縦3横2nの配列の一番左端の形状は、次の3種類。それぞれをX型、Y⁺型、Y^-型、と呼ぶことにする。
  それぞれの個数を、x_n、y⁺_n、y^-_nとすると、
  あきらかに、y⁺_n=y^-_n=1/2y_n

  X型	Y+型	Y-型
  xn	y+n	y-n
  xn	yn

• これから、縦3横2nの配列の左側に、縦3横2の長方形を付け加えて、縦3横2(n+1)の配列を作っていこうと思うのだが、このタイルの配列には、左側の縦3横2の長方形がそもそも切り離せないような配列が存在する。それらは、この方法では生成できないにもかかわらず、その数を数えなければならない。 それらは左端が次のような形状をした配列である。

  Z+型	Z-型

  これらの配列も、以下のような「1対1対応」の変換を施すことで、あたかも元来それぞれY⁺型、Y⁺型、であった縦3横2n配列の左側に、縦3横2の長方形を付け加えて生成したかのように数えることが出来るのである。

  ↓	↓

  
  
  
• さて、左端に付け加えるべき縦3横2の長方形は、以下の3種類。

  p型	q型	r型

  • 第n段階のすべての並べ方a_n=x_n+y_nに対して、第n+1段階のX型の個数、x_n+1は、ただp型長方形をつなげばよいのだから、
    x_n+1=a_n
    または、
    x_n+1=x_n+y_n
  • 第n+1段階のY⁺型の個数は、第n段階のすべての並べ方a_nにq型長方形をつなげたものだけでなく、ほかにこの方法では生成できないZ⁺型も数えなければならない。
    その個数は、上で検討したように、第n段階のY⁺型の個数y⁺_nに等しい。すなわち、
    y⁺_n+1=a_n+y⁺_n
    同様に、
    y^-_n+1=a_n+y^-_n
    したがって、
    y_n+1=2a_n+y_n
    または、
    y_n+1=2(x_n+y_n)+y_n
    y_n+1=2x_n+3y_n
  
  
  
• これらをa_nについての隣接3項間漸化式にすると、
  
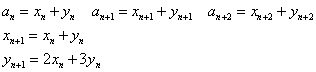
  であるから、
  
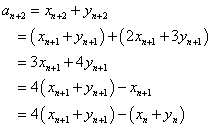
  すなわち、
  
  
  
• 初項、a₁,a₂を求めよう。
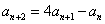
  • n=1のとき、すなわち、縦3横2の長方形は、明らかに次の3通り。
    
    
  • n=2のとき、すなわち、縦3横4の長方形は、
    まず、X型、nのときのすべてに、p型をつなげて、3通り。 まず、Y⁺型のうち、nのときのすべてに、q型をつなげて、3通り。 この他に、上の表の真ん中のものを「変換」して得られたものが1通り。

    →

    同様に、Y^-型のうち、nのときのすべてに、r型をつなげて、3通り。 この他に、上の表の右側のものを「変換」して得られたものが1通り。

    →

    合計11通り。
• 漸化式を解く。
  
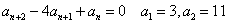
  次のように仮定して係数比較すると、
  
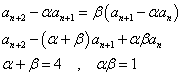
  「2次方程式の解と係数の関係」より、α、βは次のような2次方程式の解であることがわかる。α、βの大小関係を次のように仮定して、
  
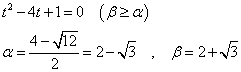
  こうして、
  
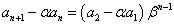
  また、α、βは入れ替え可能であるから、
  
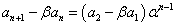
  両辺を引き算して、
  
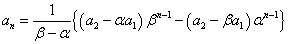
  数値を代入すると、
  
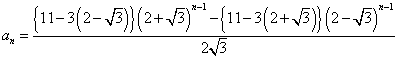
  すなわち、
  
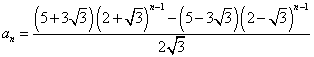
  が、得られた。
  確かめてみよう。もちろん、コンピュータの力を借りて！

  n	an
  1	3
  2	11
  3	41
  4	153
  4	571
  6	2131
  7	7953
  8	29681
  9	110771
  10	413403
  ・・・	・・・

  ---

• 次に、
  
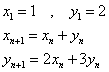
  として、連立漸化式を解いてみる。
  次のように置き、
  
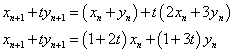
  1:t=1+2t:1+3tとなるような定数tを定める。
  
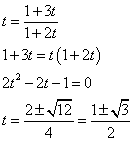
  この2つの解を、それぞれα、βとしよう。
  
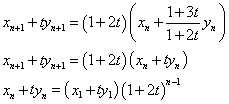
  であるから、
  
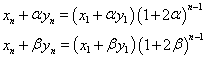
  両辺引き算をして、
  
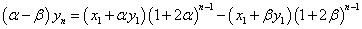
  こうして、y_nが得られる。
  
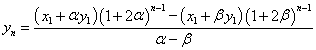
  同様に、次のようにして両辺を引き算すると、
  
  
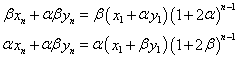
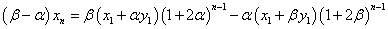
  こうして、x_nも得られる。
  
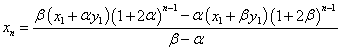
  数値を代入する。
  
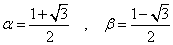
  とすると、
  
  
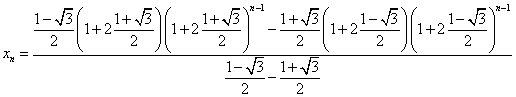
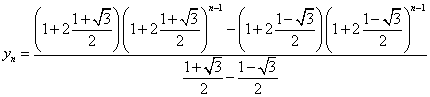
  さらに、
  
  
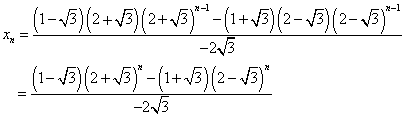
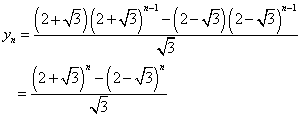
  a_n=x_n+y_nであるから、
  
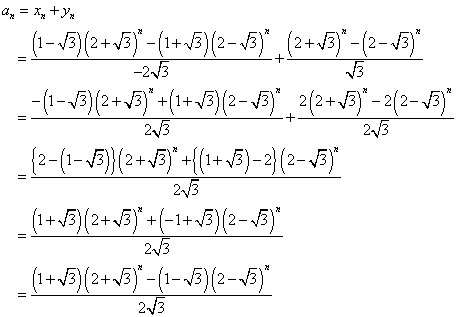
  これは、次のように変形できるから、上の結果と同じになった。
  
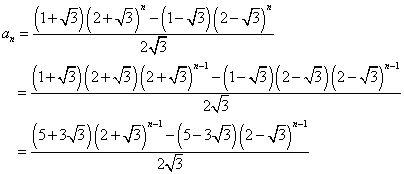
  計算結果は、以下の通り。

  n	xn	yn	an
  1	1	2	3
  2	3	8	11
  3	11	30	41
  4	41	112	153
  5	153	418	571
  6	571	1560	2131
  7	2131	5822	7953
  8	7953	21728	29681
  9	29681	81090	110771
  10	110771	302632	413403

  なるほど、
  x_n+1=x_n+y_n
  y_n+1=2x_n+3y_n
  であることが、よくわかる！
  で、縦3横20の長方形を、1×2のタイルで敷き詰める方法が、413403通りであることが、わかったわけである（笑）。それがどうした？
  
  
  
  

  ---

• さらに、
  
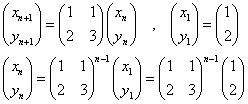
  であることから、この係数行列のn乗を求めることによって、計算する。
  
  
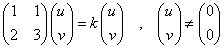
  となる定数k(固有値)、ベクトル(u,v)(固有ベクトル)を求める。
  
  
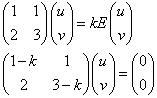
  であるから、このような零ベクトルでない(u,v)が存在するのは、左辺の行列が逆行列を持たない場合に限られる。
  すなわち、
  
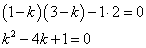
  となり、この方程式（固有方程式）は、驚くべきことに、a_nの「特性方程式」と同じになってしまった！
  
  
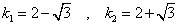
  として、それぞれに対応する固有ベクトルを求める。
  
  
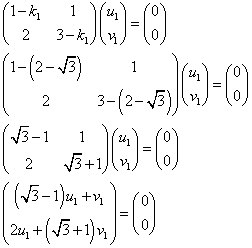
  であるから、
  
  
  
  
  
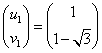
  同様に、
  
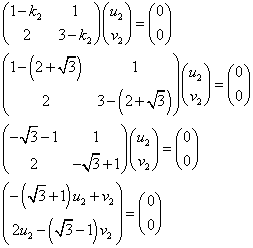
  であるから、
  
  
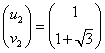
  ここで、
  
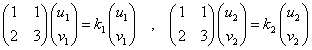
  であるから、
  
  
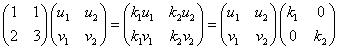
  すなわち、
  
  
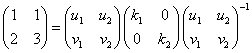
  固有方程式が、異なる2解をもつ以上、2つの固有ベクトルは「1次独立」であり、したがって、それを並べた行列は逆行列をかならず、もつ。
  
  
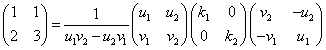
  すなわち、
  
  
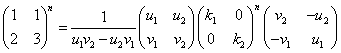
  対角行列は容易にn乗を求めることができ、
  
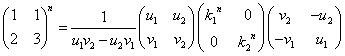
  となる。数値を代入しよう。
  
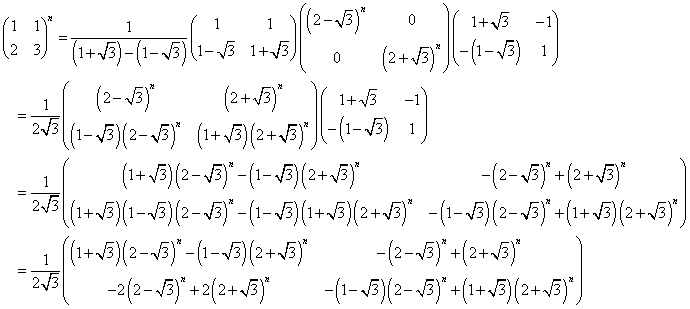
  すなわち、
  
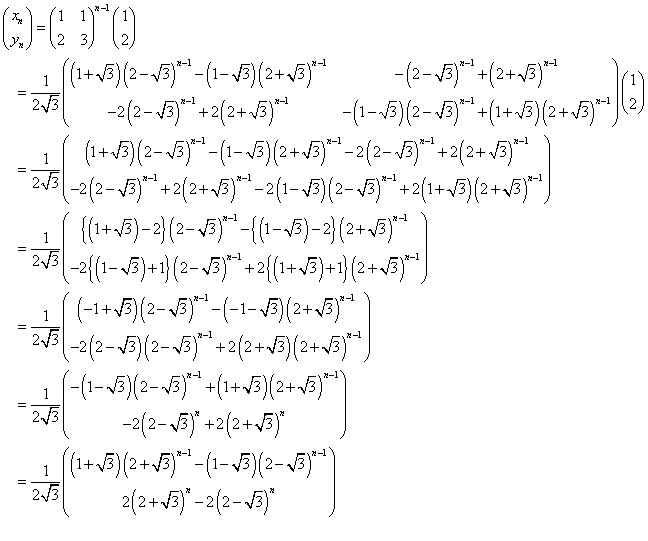
  となり、同じ結果を、得た。