• 3次関数のグラフはただ一つの変曲点をもち、かつ、その点に関して対称であることを示す。
  f(x)=ax³+bx²+cx+d
  f'(x)=3ax²+2bx+c
  f''(x)=6ax+2b
  であるから、1次方程式f''(x)=0はただ一つの解を有する。
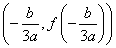  が、変曲点である。
• y=f(x)のグラフに対して、この点が原点になるようにこれを平行移動して得られた曲線のグラフをy=g(x)とし、
  y=g(x)が、原点に関して対称、すなわち、g(x)が奇関数であることを示せばよい。
  一般に、点(p,q)が、原点(0,0)に重なるように移動するには、x軸方向に-p、y軸方向に-q平行移動することを要するから、
  y+q=f(x+p)
  ここでは、
  
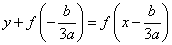
  すなわち、
  
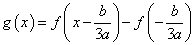
  計算すると、
  
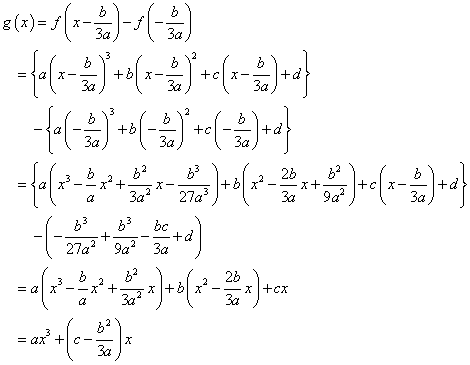
  ここで、g(-x)=-g(x)であるから、g(x)は奇関数である。