---

• 3次関数  f(x)=ax³+bx²+cx+d  (ただしa0)  のグラフCは、C上のある点P(p,f(p))に関して点対称であることを示し、この点を求めよ。

  ---

  任意のxに対し、(x,f(x))のP(p,f(p))に関する対称点(X,Y)
  
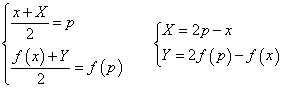
  がC上にあるようなpが存在することを示す。
  
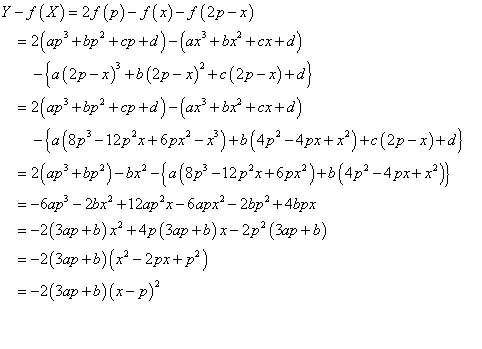
  3ap+b=0のとき、任意のxに対してY=f(X)が成立する。
  すなわち、Cは、
  
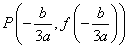
  に関して点対称であることが示された。

  ---

• 3次関数  f(x)=ax³+bx²+cx+d  (ただしa0)  が、極値をもつ条件を求めよ。

  ---

  f'(x)=3ax²+2bx+c
  2次方程式  f'(x)=0  が異なる2個の実数解をもてばよいから、
  b²-3ac＞0

  ---

• Cのグラフを、Pが原点に重なるように平行移動して得られたグラフC'をあらわす関数を、y=g(x)とする。g(x)を求めよ。
  また、g(x)が極値をもつ条件を求めよ。

  ---

  x軸方向に、b/3a、y軸方向に、-f(-b/3a)平行移動する。
  
  
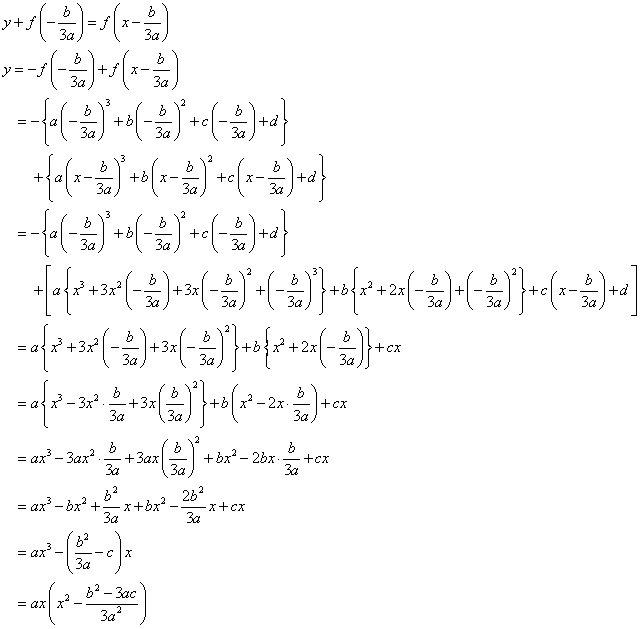
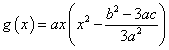
  g(x)が極値をもつ条件も、
  b²-3ac＞0
  である。

  ---

• f(x)が極値をもつとき、極値を与えるxを、 α , β とする。C上の点 Q( α , f(α) ) , R( β , f(β) )は、点P( p , f(p) )に関して対称であることを示せ。

  ---

  
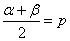    に対して、 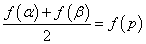   であることを示したい。
   α , β は、2次方程式 f'(x)=0 すなわち、3ax²+2bx+c=0の解であるから、
  
  
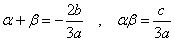
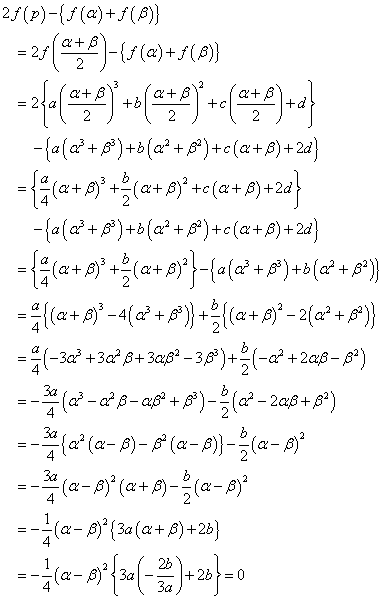
  示された。

  ---

• f(x) = f(α)  となるxのうち、x=α以外のもの  x=α'  を求めよ。
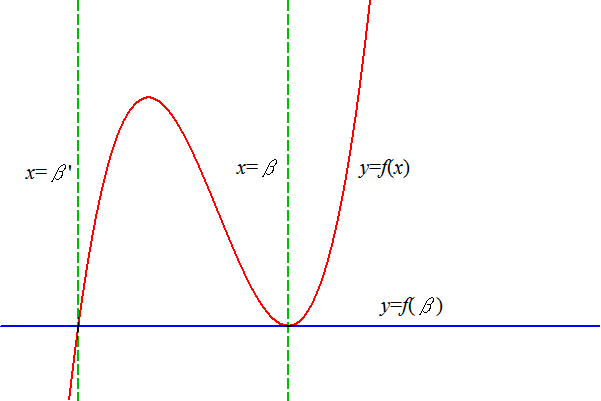
  f(x) = f(β)  となるxのうち、x=β以外のもの  x=β'  を求めよ。

  ---

  
  
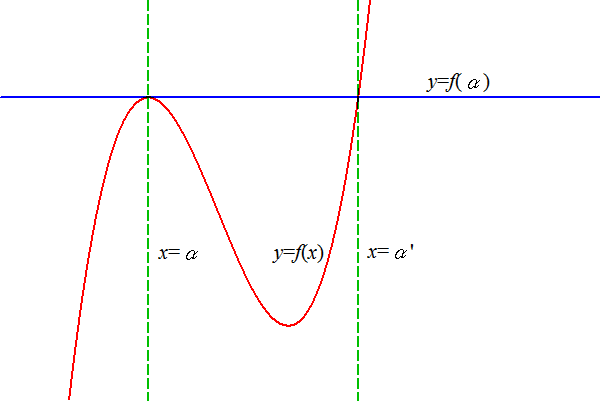
  3次方程式  f(x) = f(α)  の解のうち、  x=α  (重解)以外の解  x=α'  を求めたい。
  
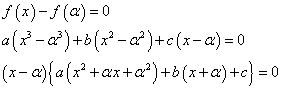
  ここで、
  
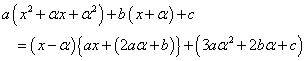
  であるから、
  
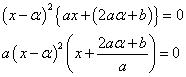
  したがって、
  
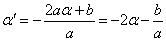
  かつ、
  3aα²+2bα+c=0
  これは、  f ' (α) = 0  という、当然のことをあらわしている。
  
  同様に、3次方程式  f(x) = f(β)  の解のうち、  x=β  (重解)以外の解  x=β'  を求めたい。
  
  

  ---

• P点のx座標をx₀とするとき、β' , α , x₀ , β , α' が、等間隔に並んでいることを示せ。

  ---

    
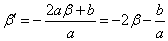
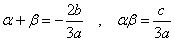
  であるから、これら5個の数値を、αを用いて表すと、
  
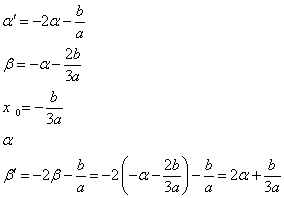
  それぞれの差を求めると、
  
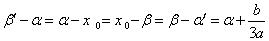
  よって、示された。
  

  ---

• g(x)が極値をもつとき、極値を与えるxを、 α , β とする。C'上の点 Q( α , f(α) ) , R( β , f(β) )は、原点に関して対称であることを示せ。
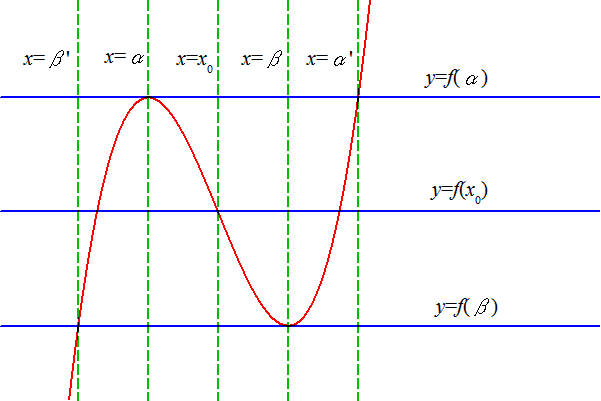
  g(x) = g(α)  となるxのうち、x=α以外のもの  x=α'  、
  g(x) = g(β)  となるxのうち、x=β以外のもの  x=β'  、とするとき、
  β' , α , 0 , β , α' が、等間隔に並んでいることを示せ。

  ---

  
  g(x)が極値をもつから、
  b²-3ac＞0
  
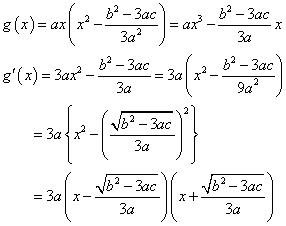
  したがって、
  
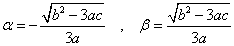
  と見ることができる。
  ところで、g(x)は奇関数であるから、C'は原点に関して対称であり、
  
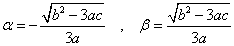
  に対して、C'上の点 Q( α , f(α) ) , R( β , f(β) )も、原点に関して対称である。
  ここで、
  
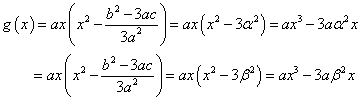
  とかけるから、
  
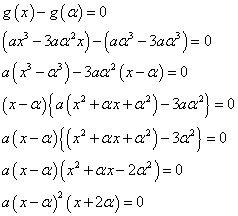
  すなわち、 α ' = -2 α 
  同様に、
  
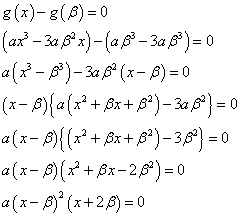
  すなわち、 β ' = -2 β 
  さらに、 β = - α であるから、
  β' , α , 0 , β , α' は、それぞれ間隔| α |で並んでいることがわかる。