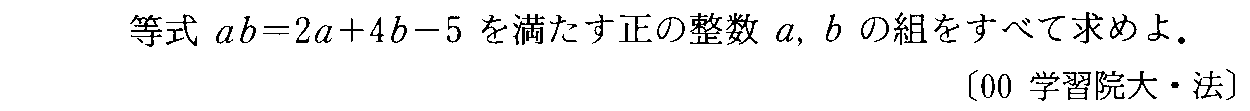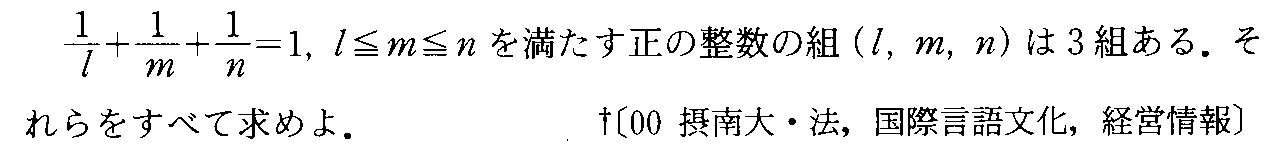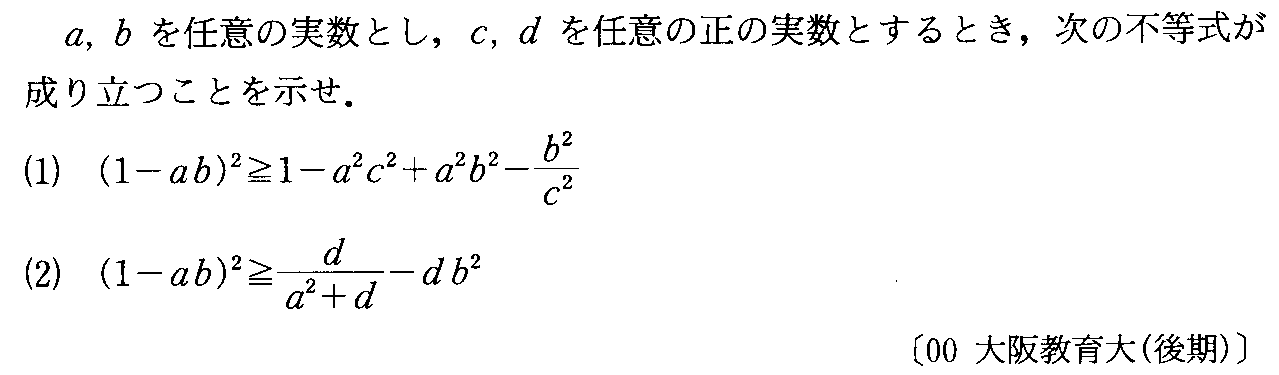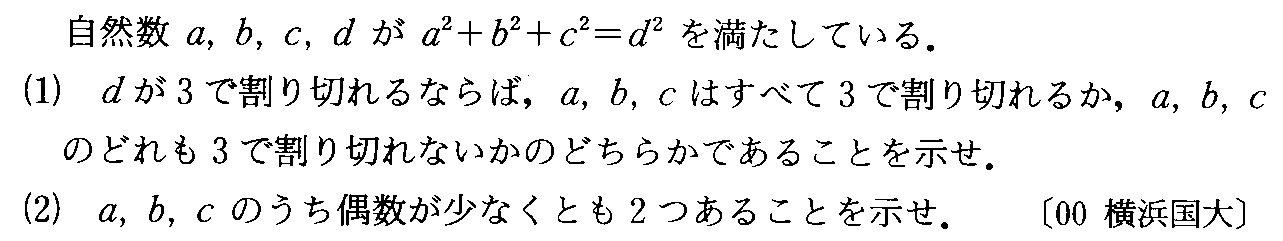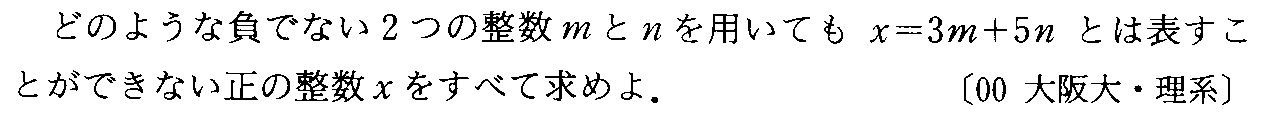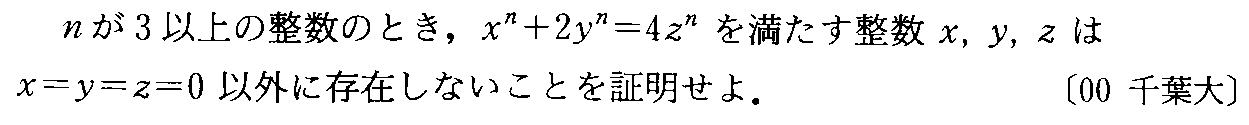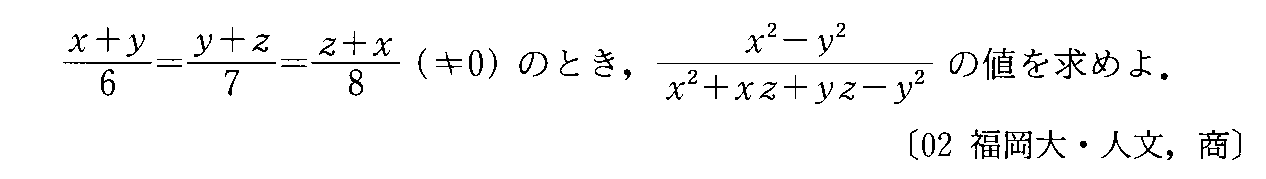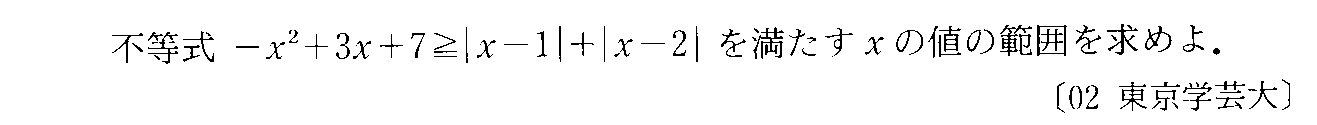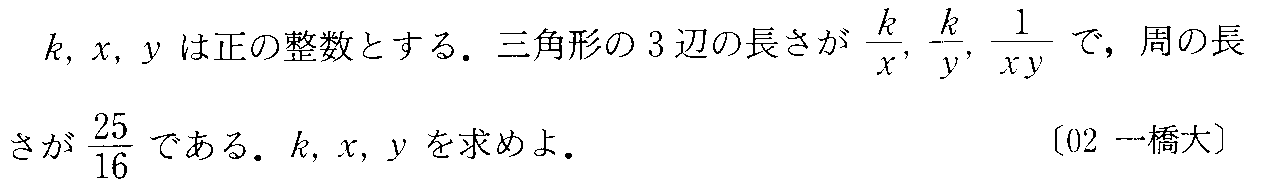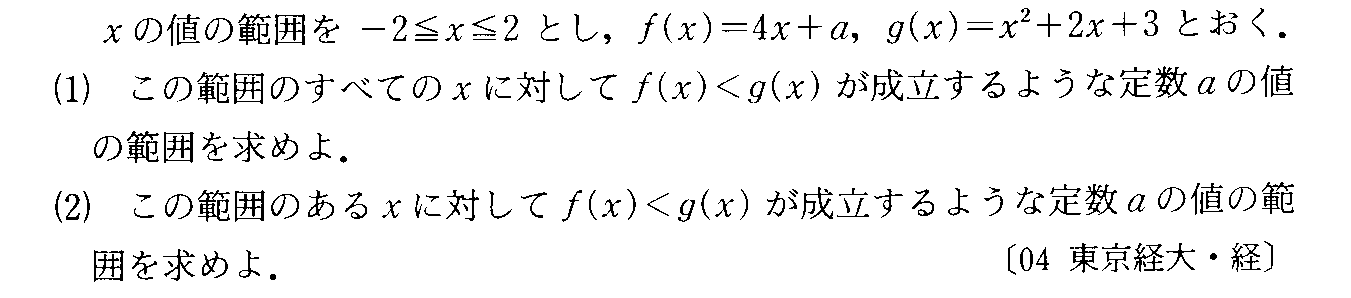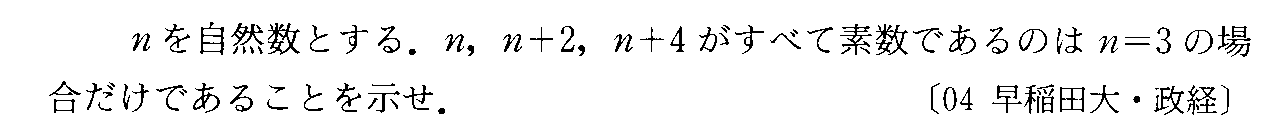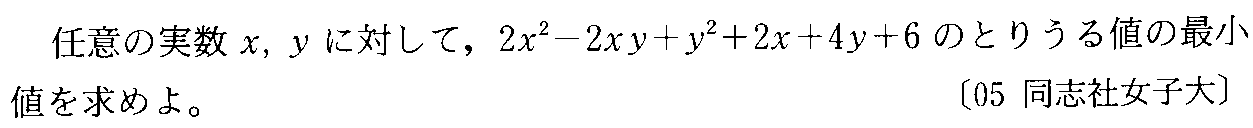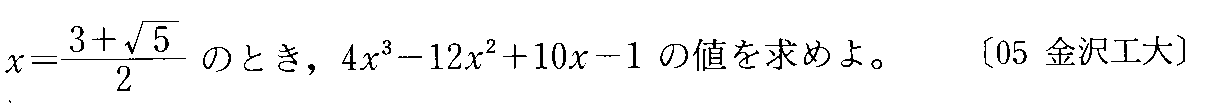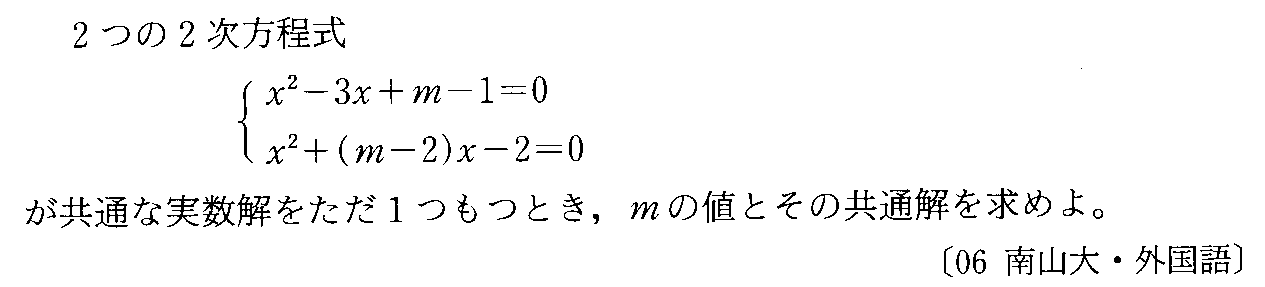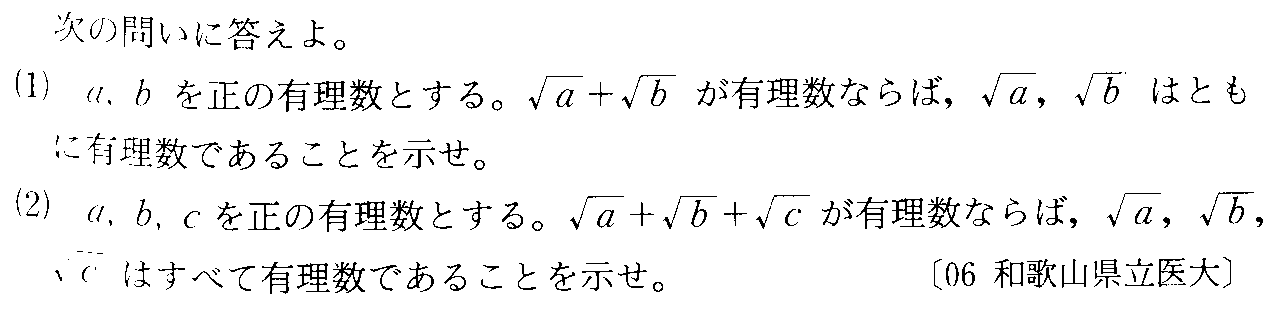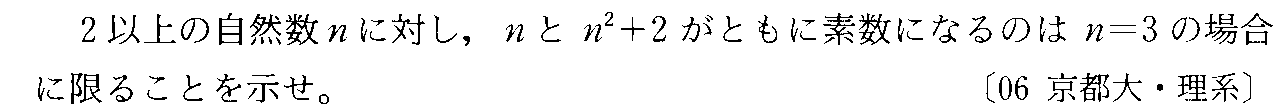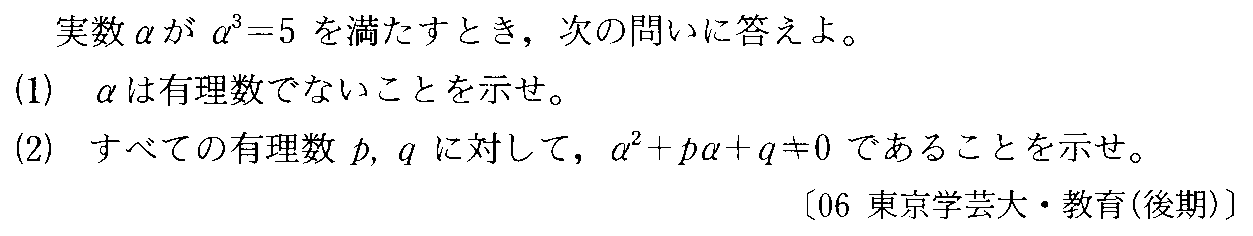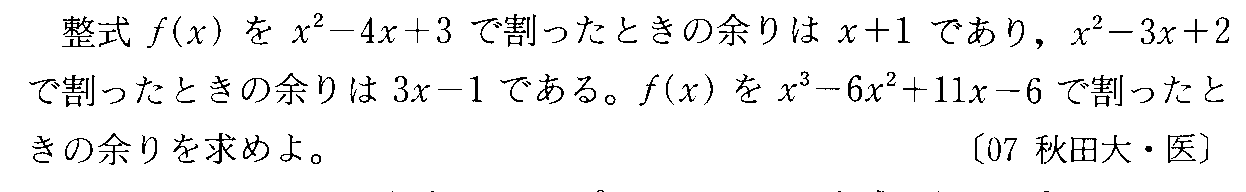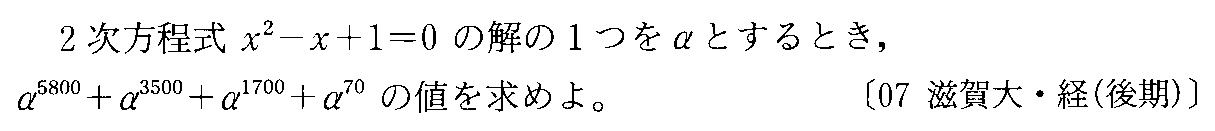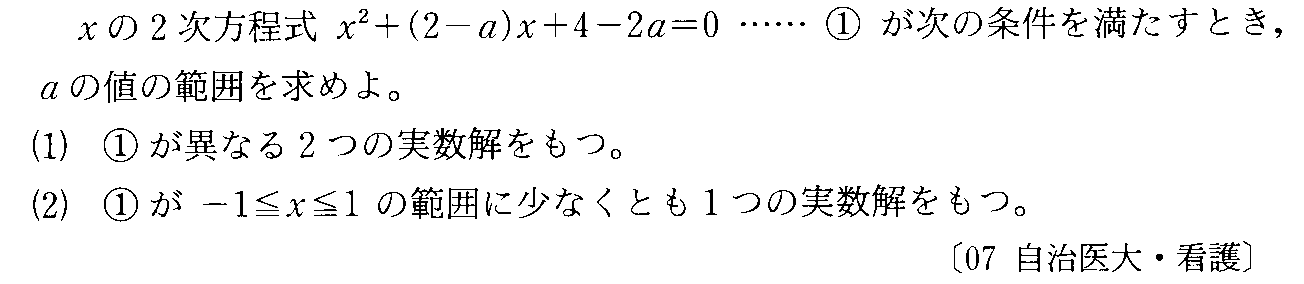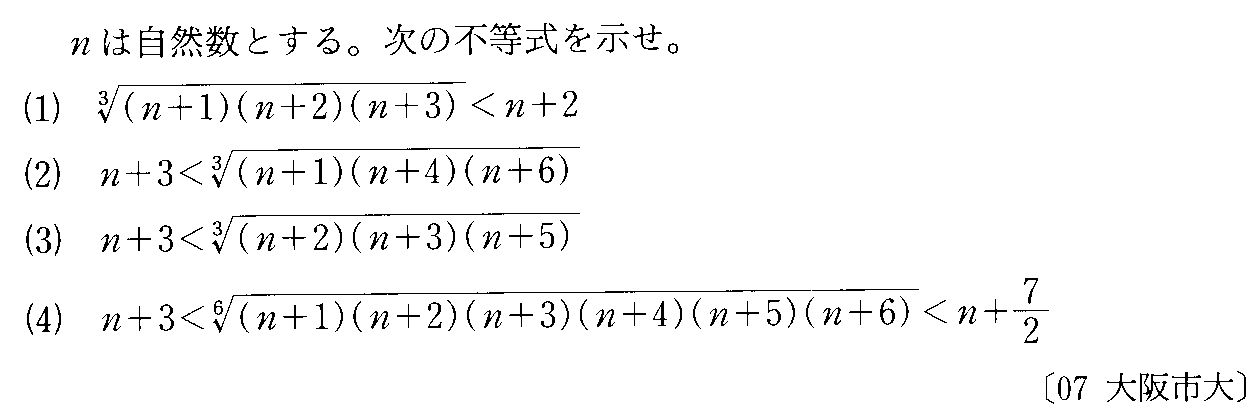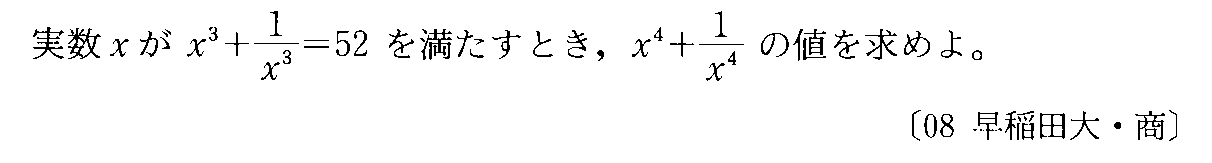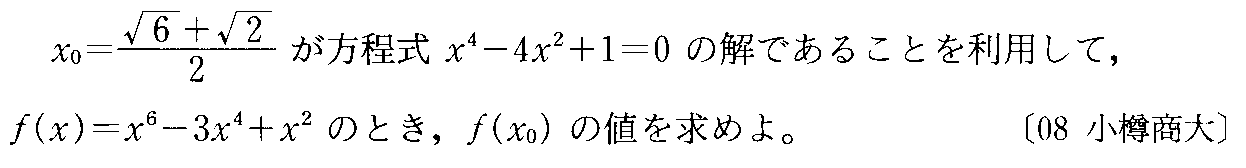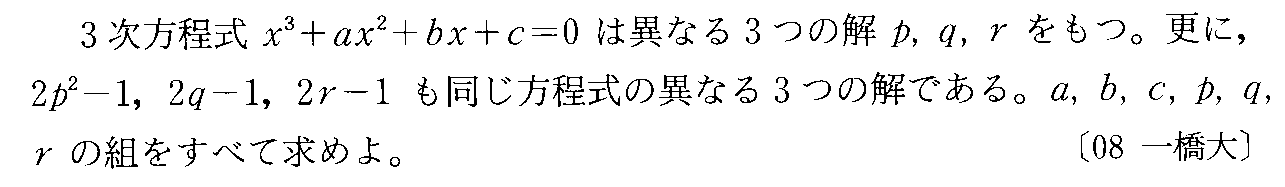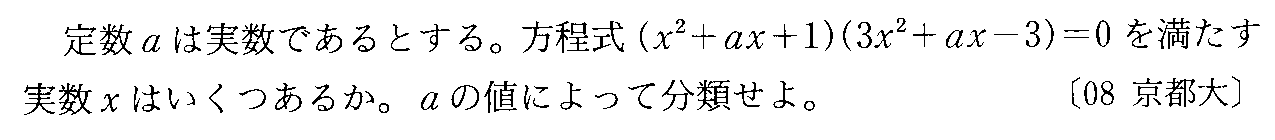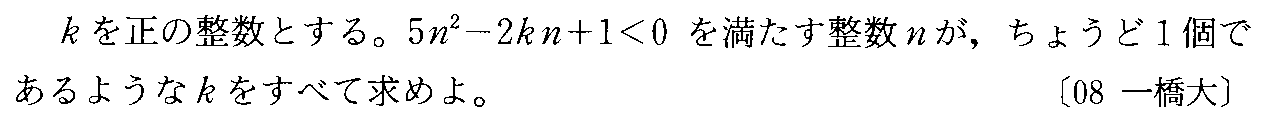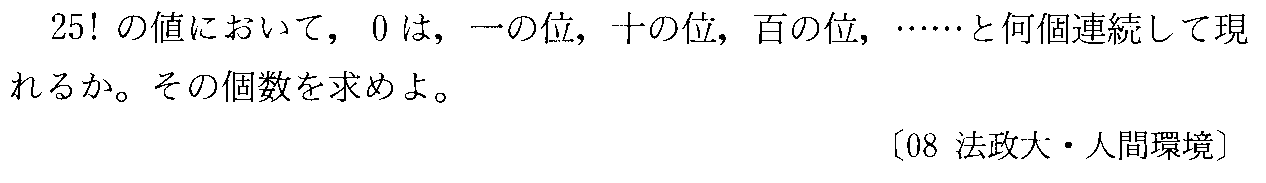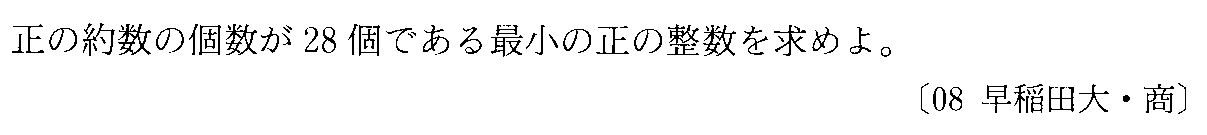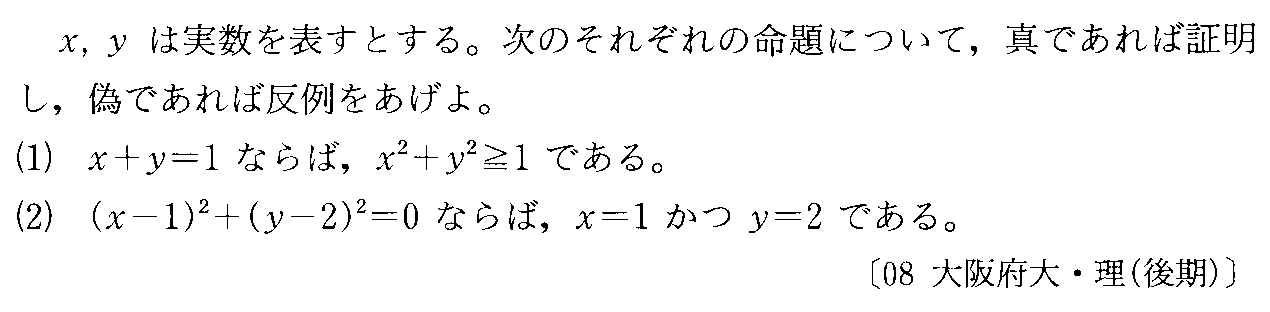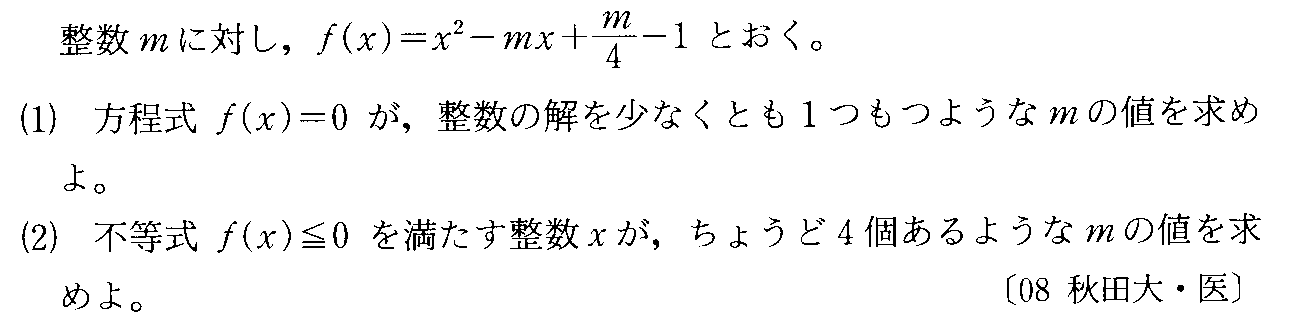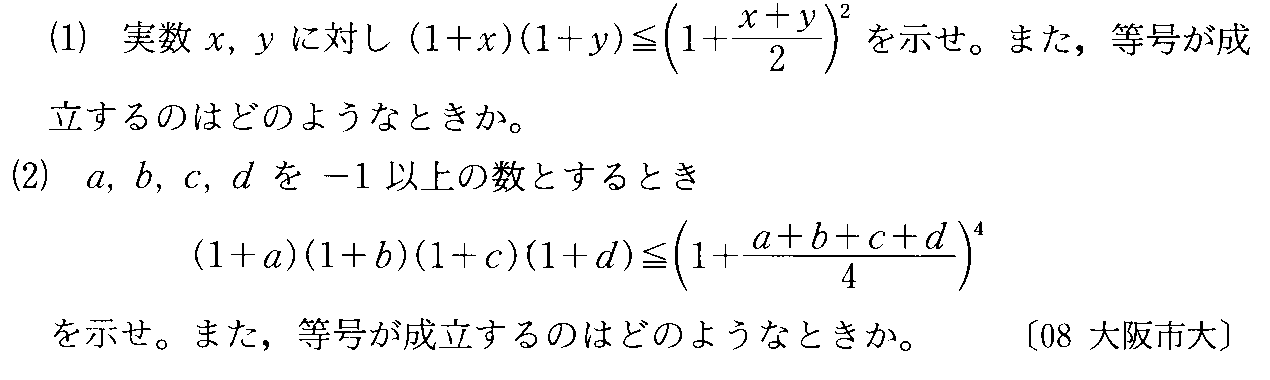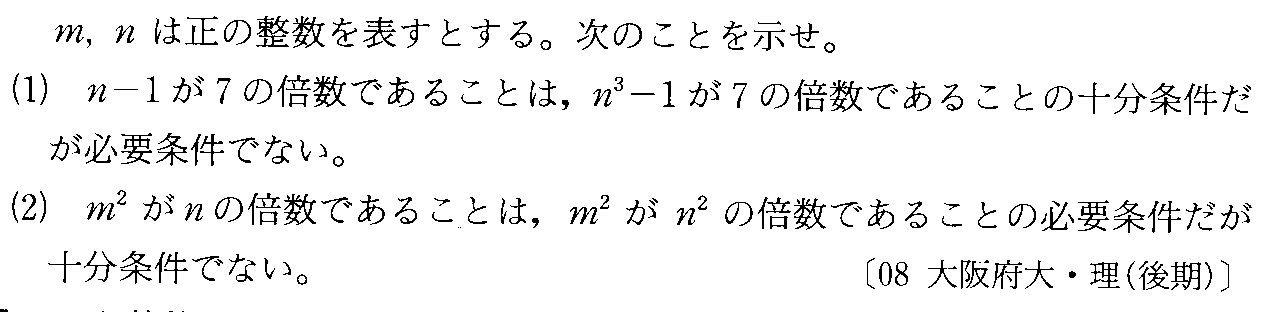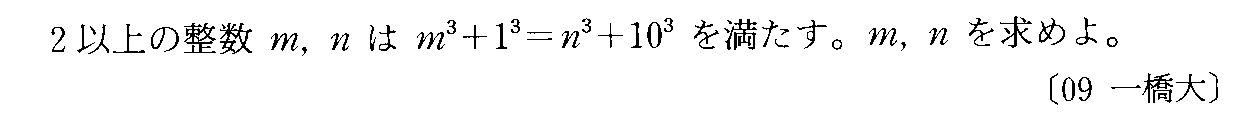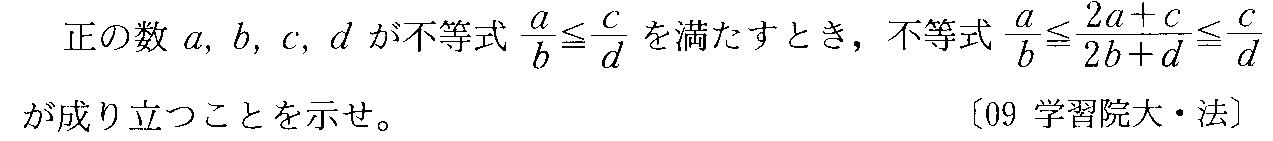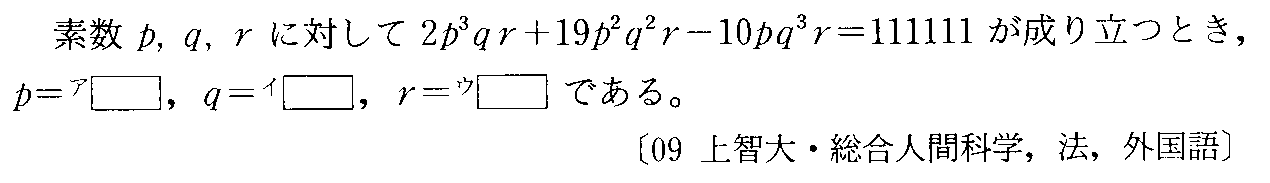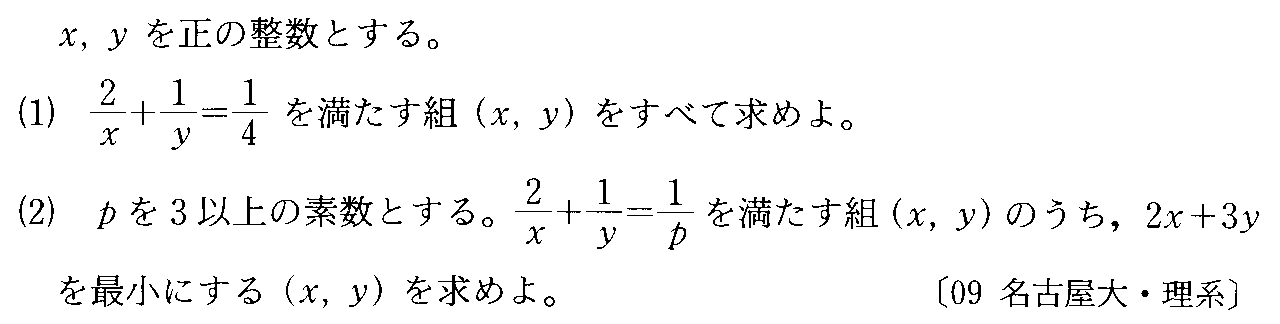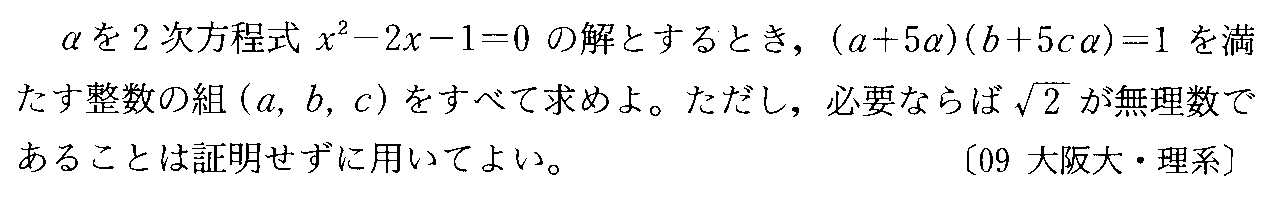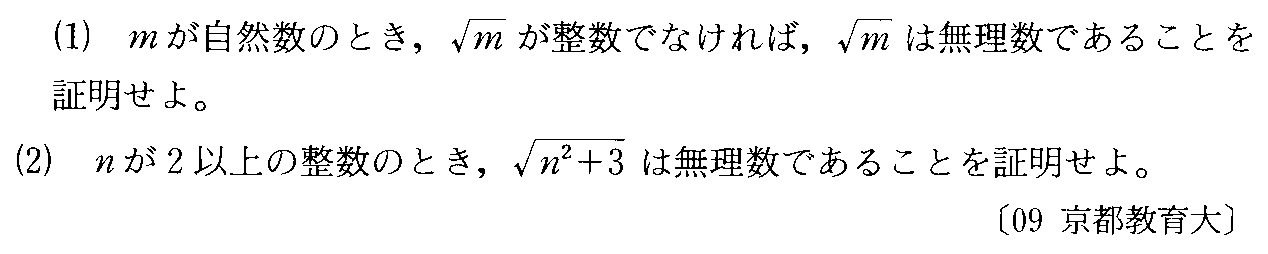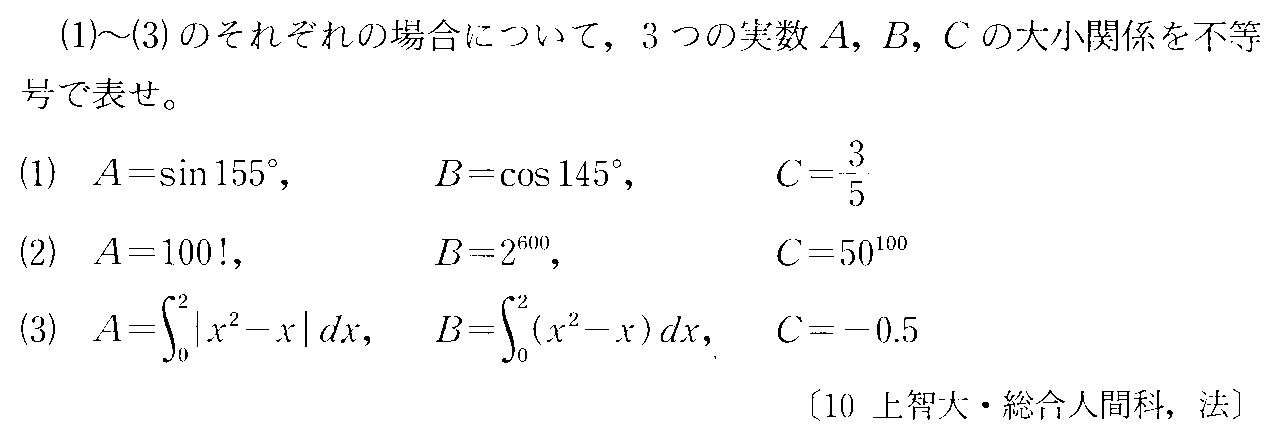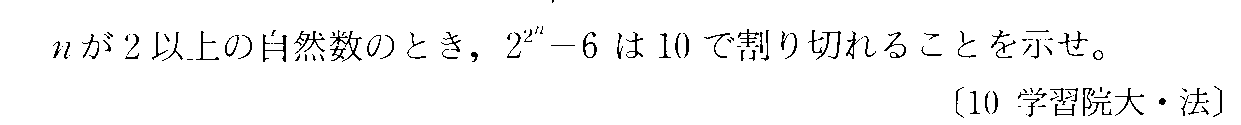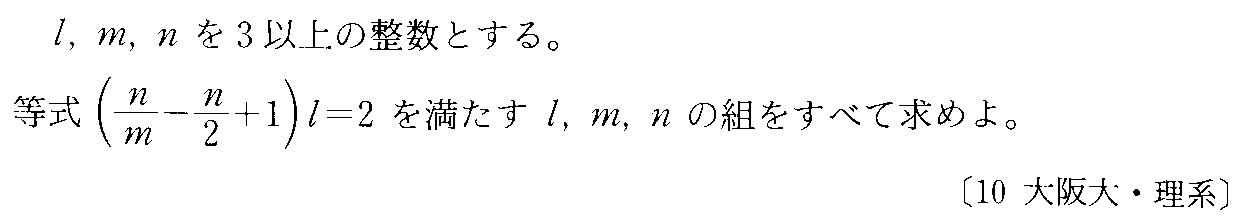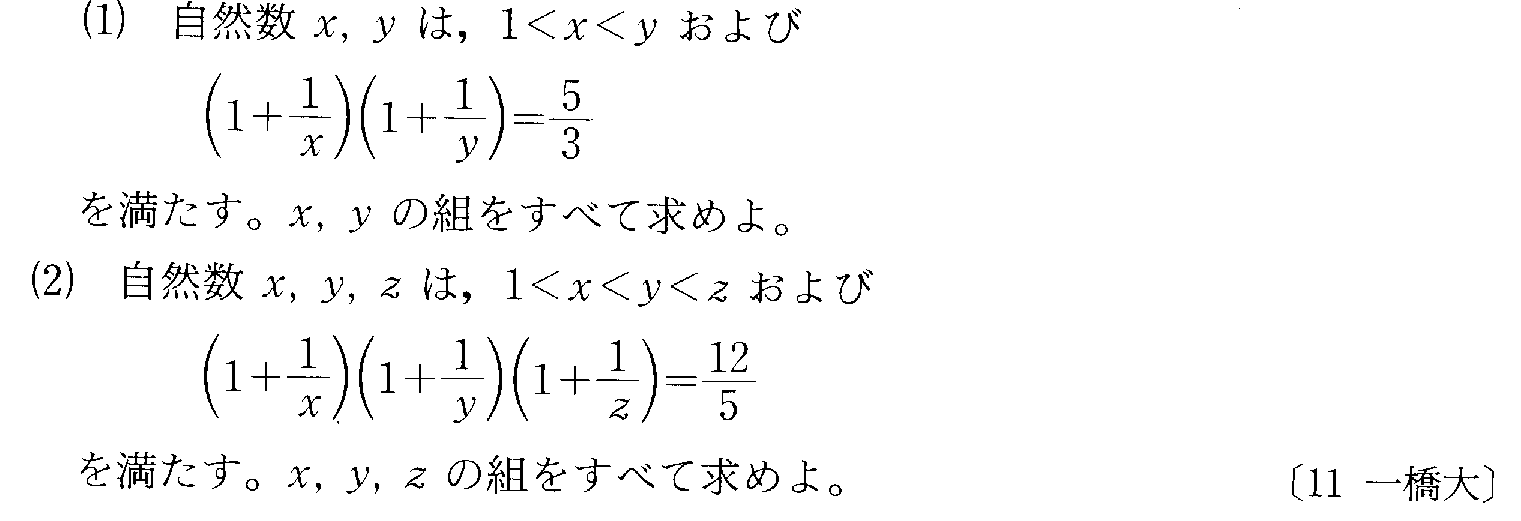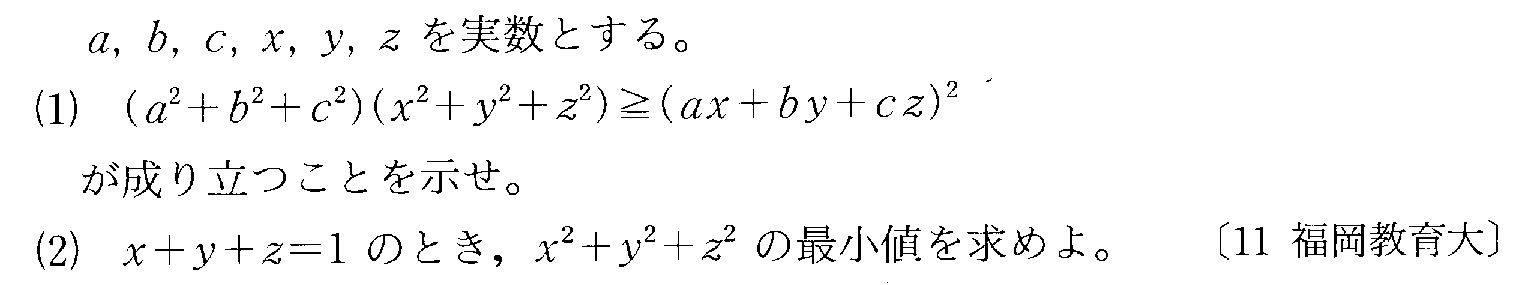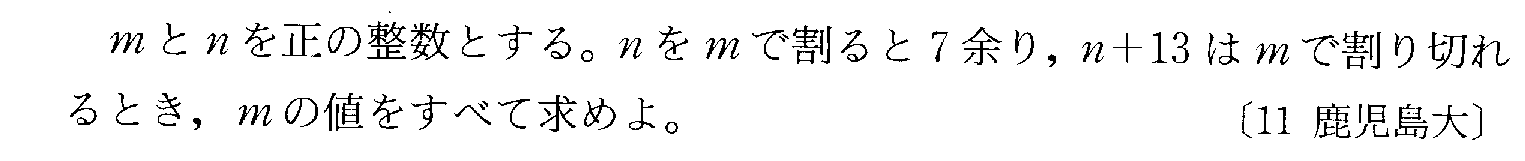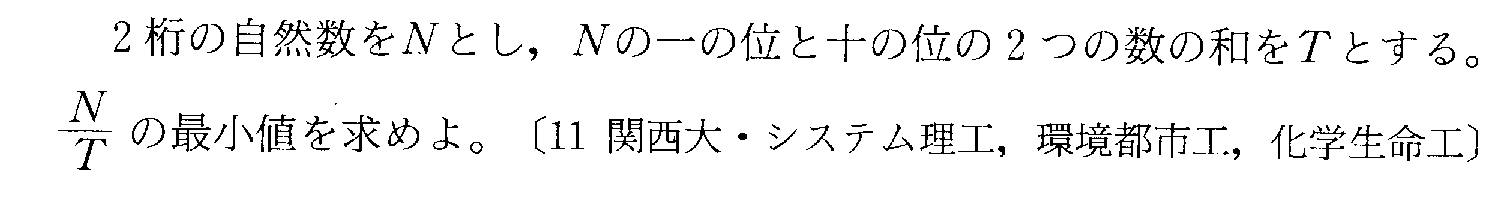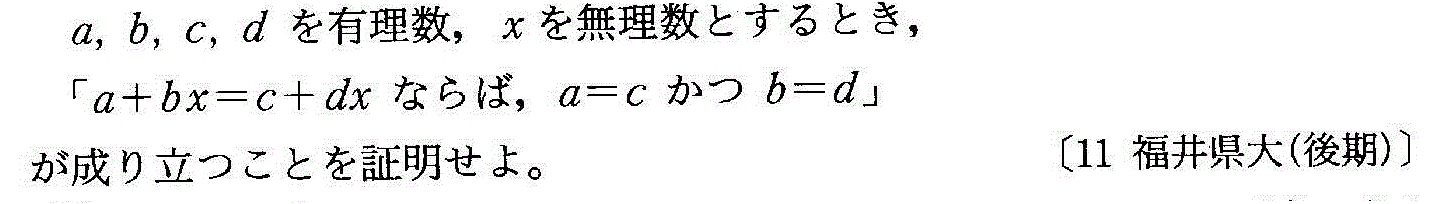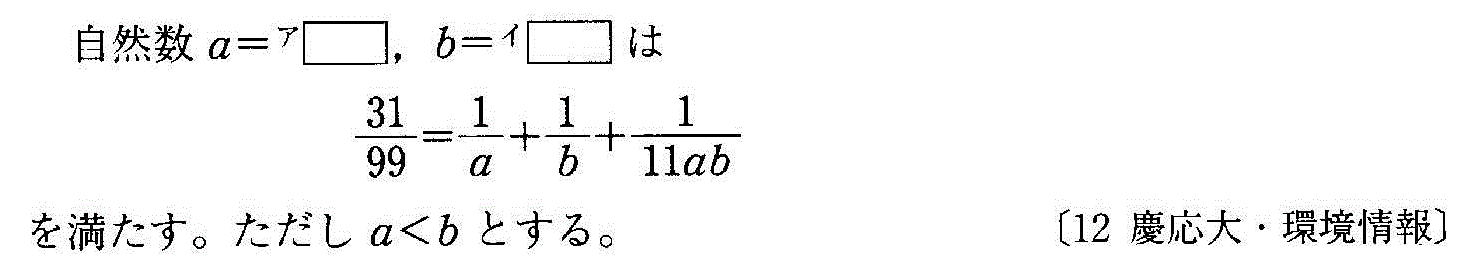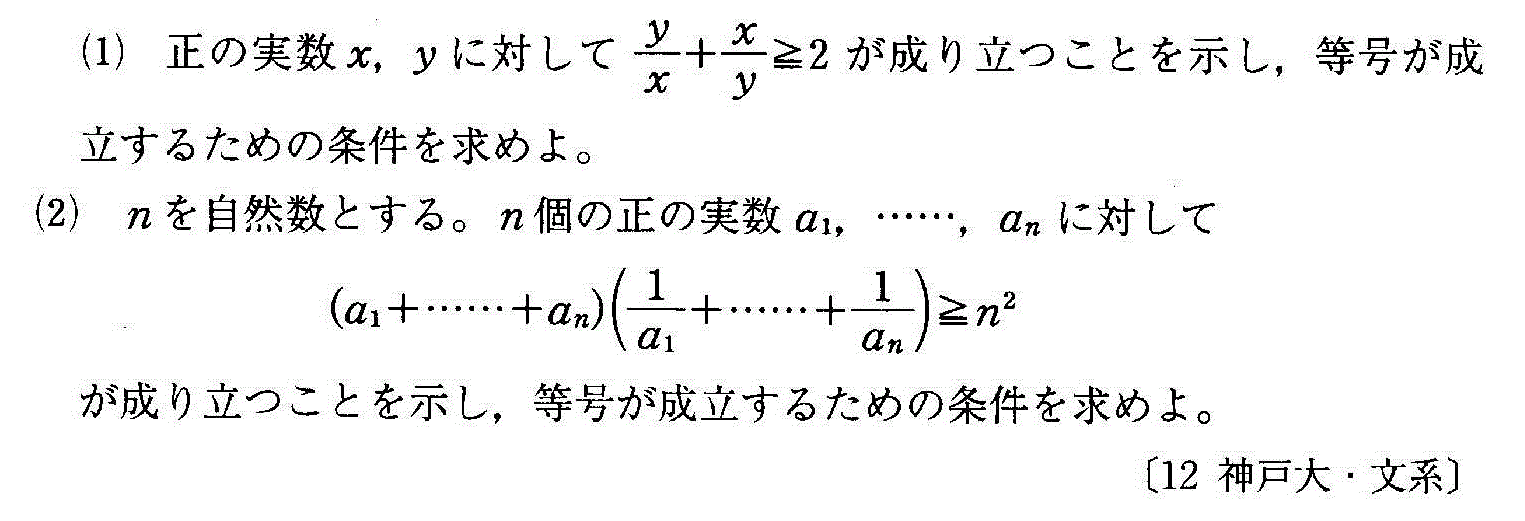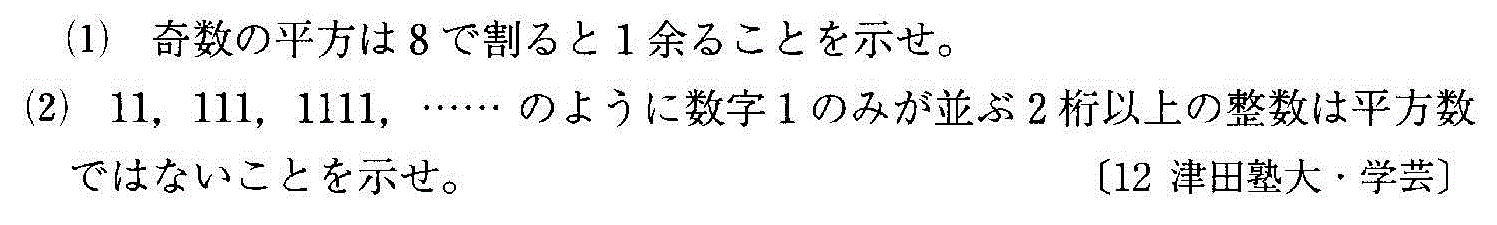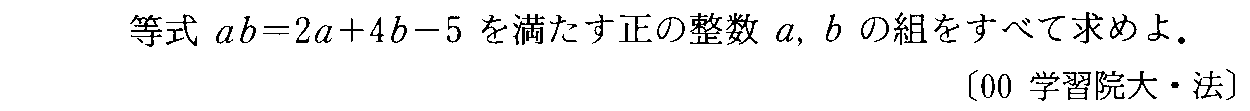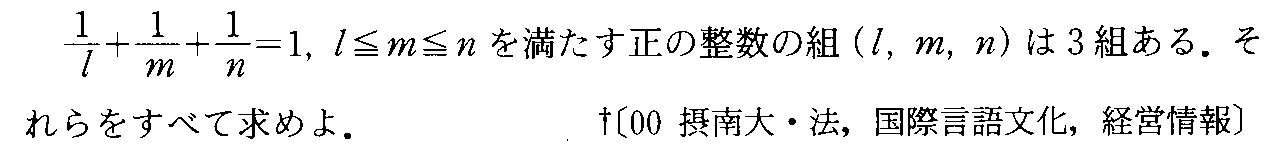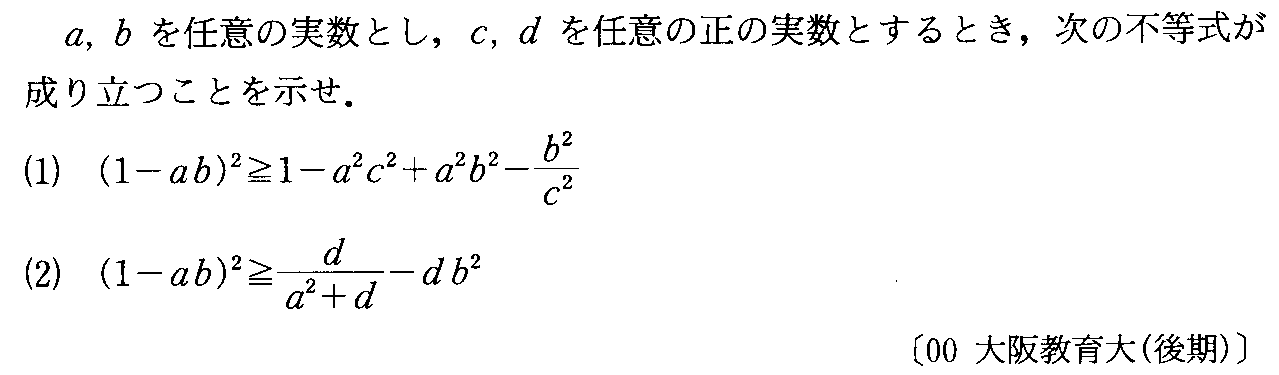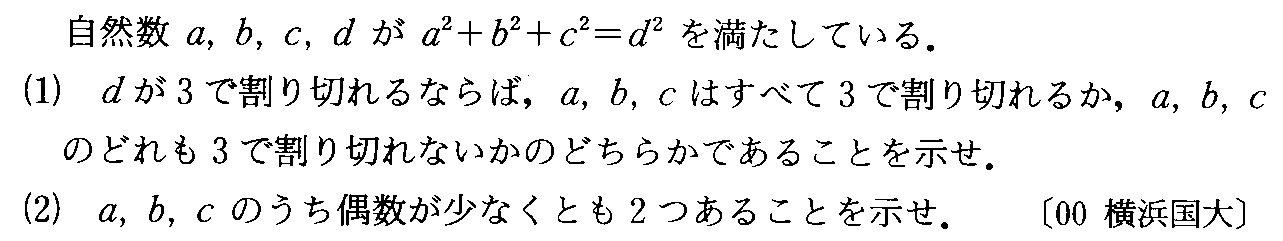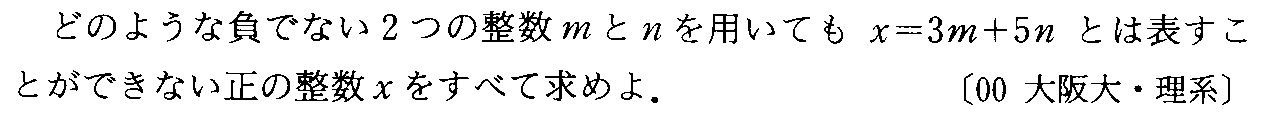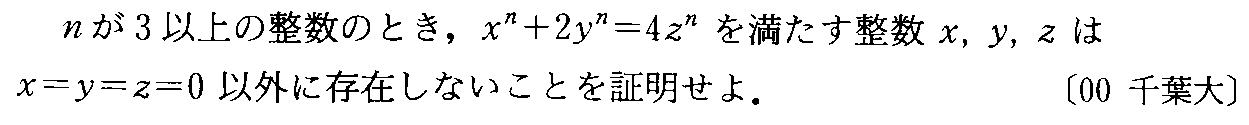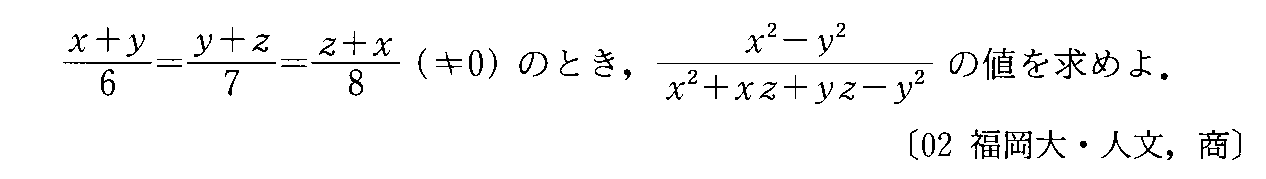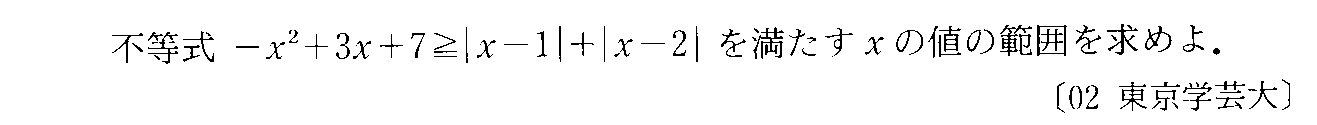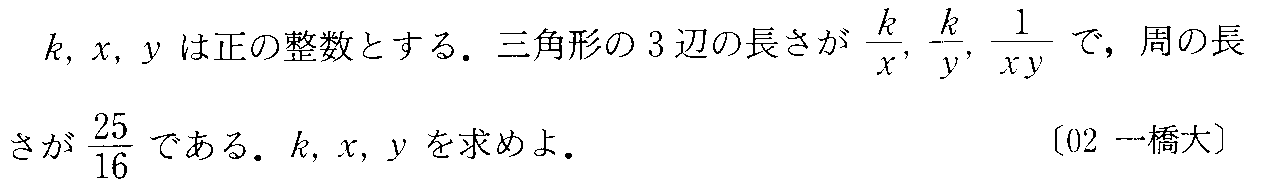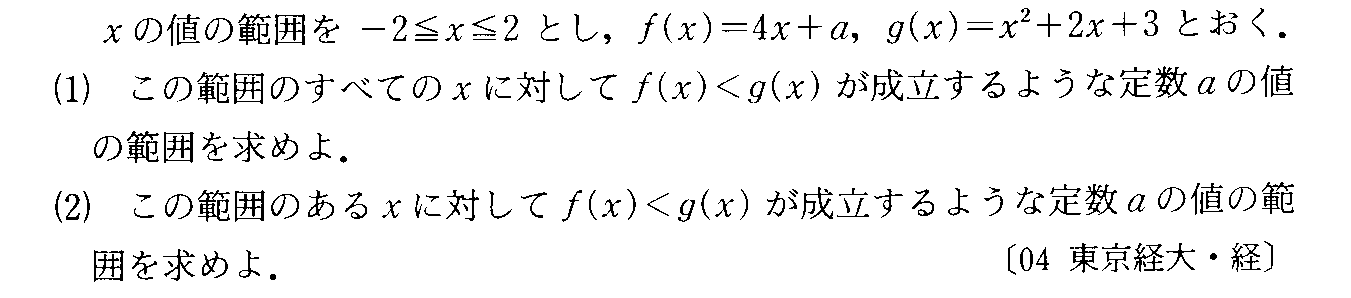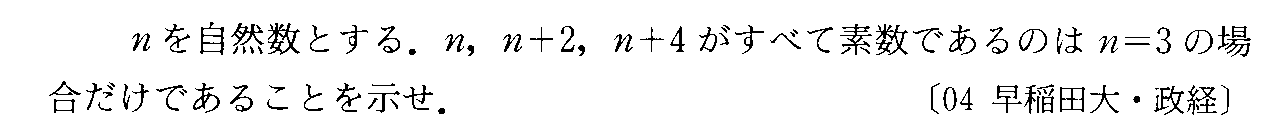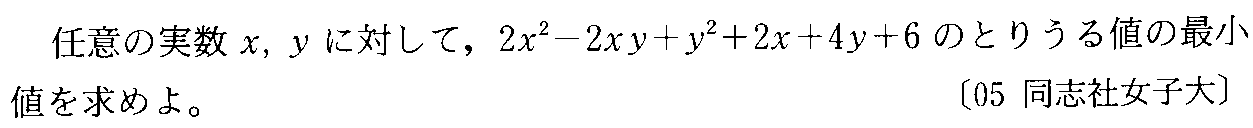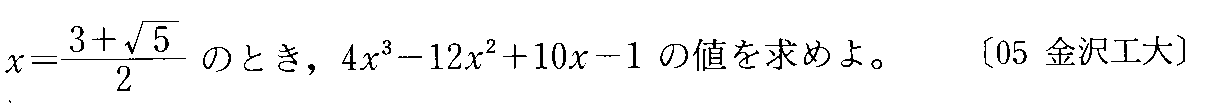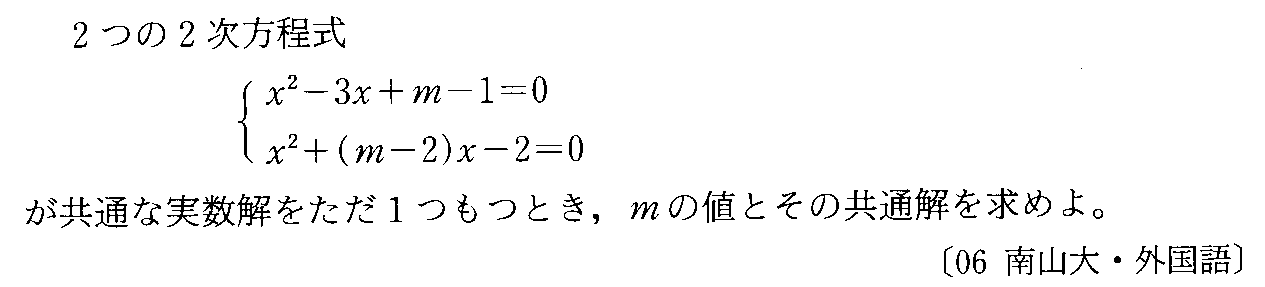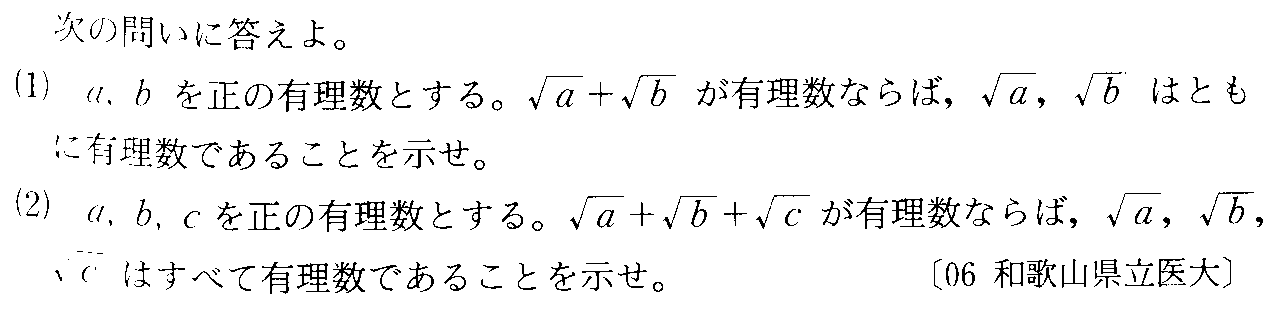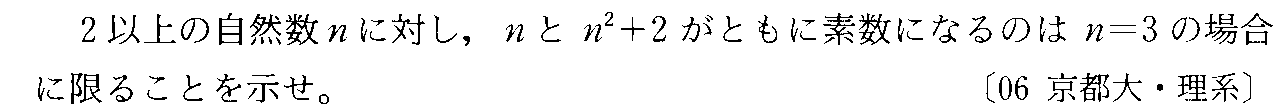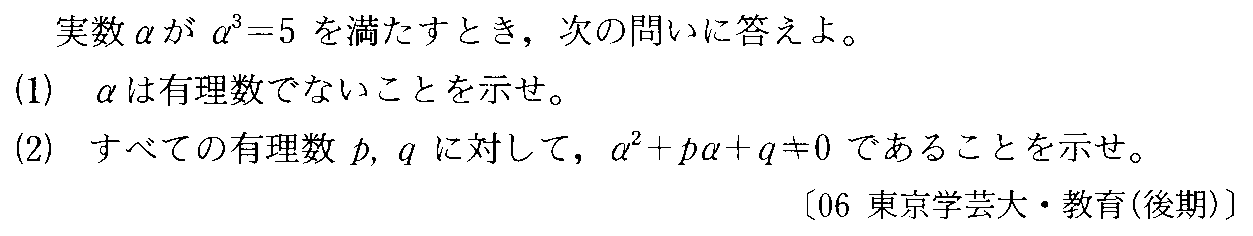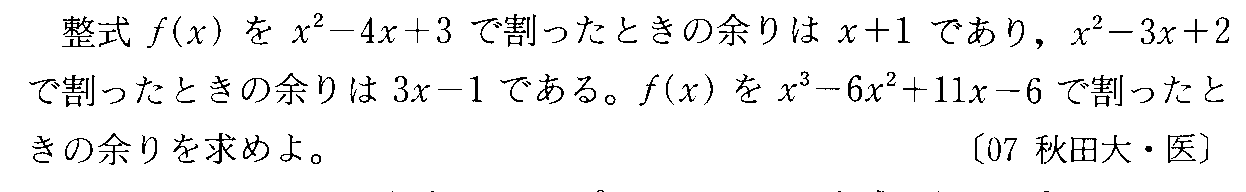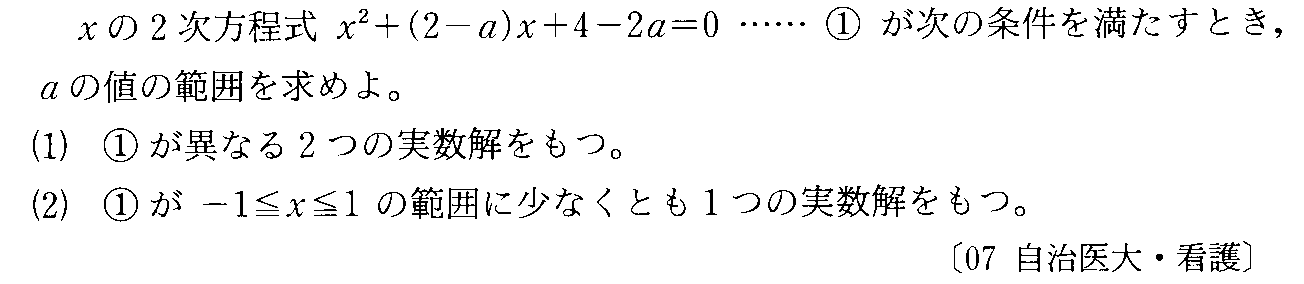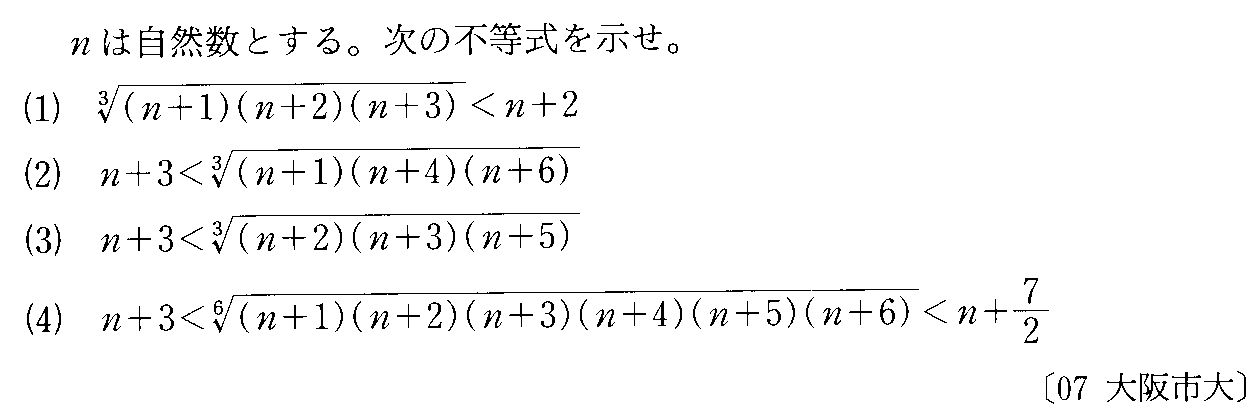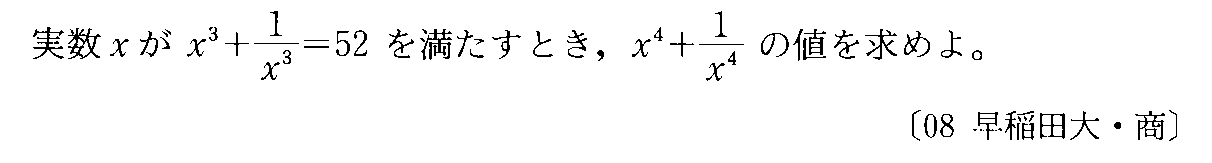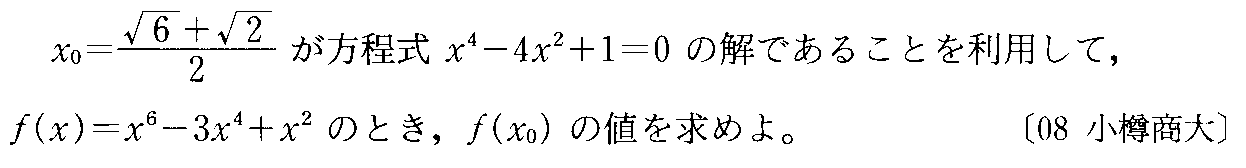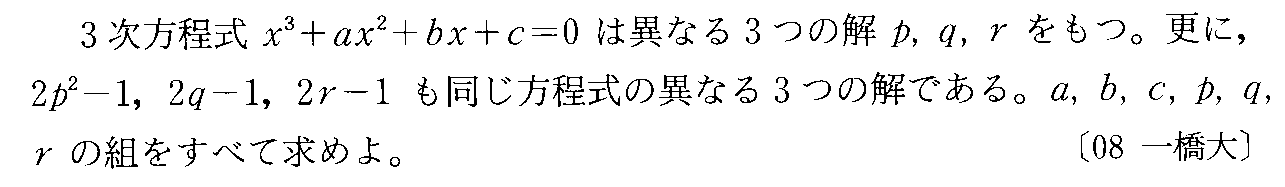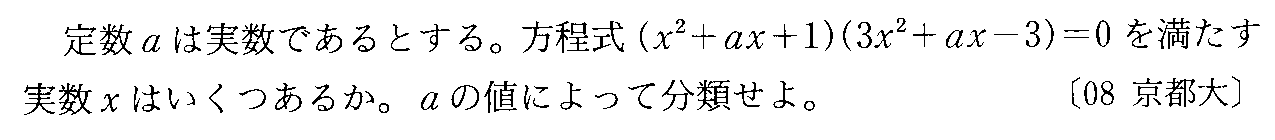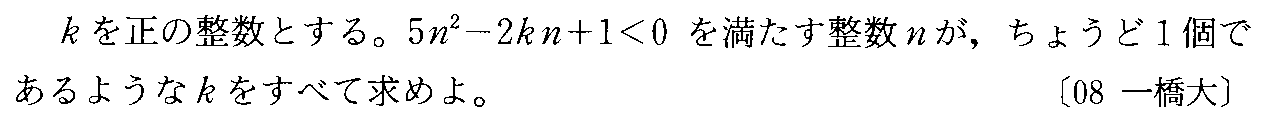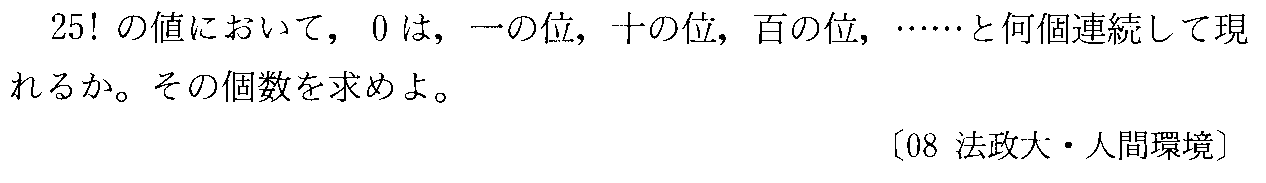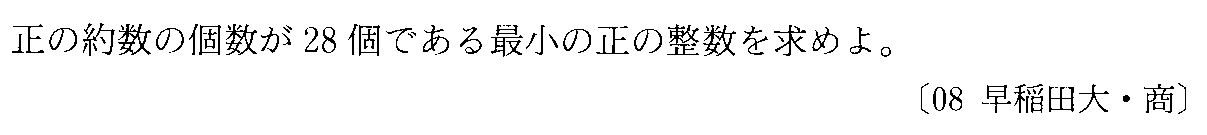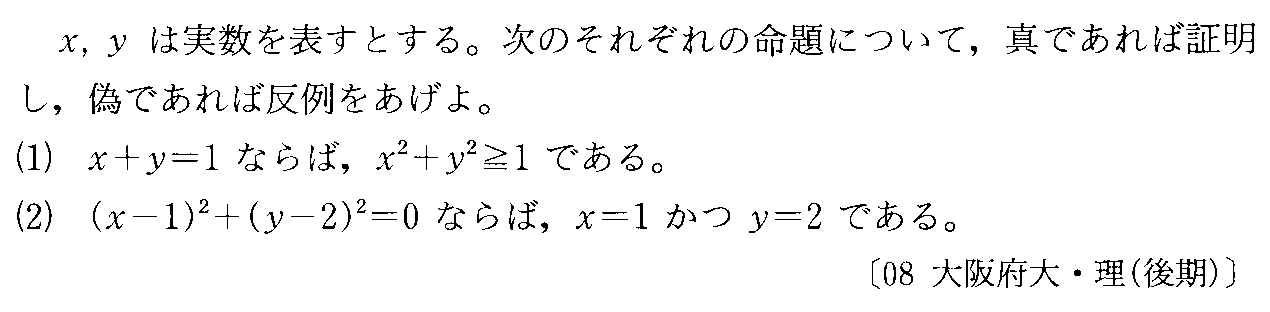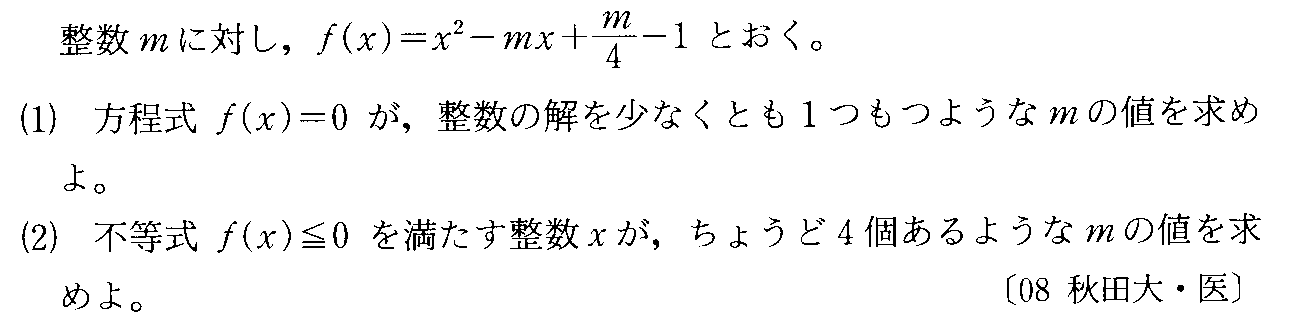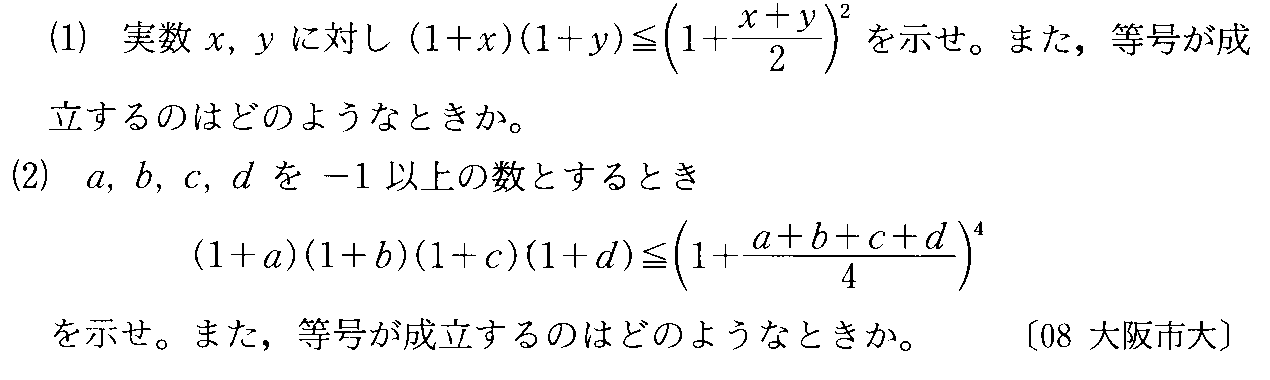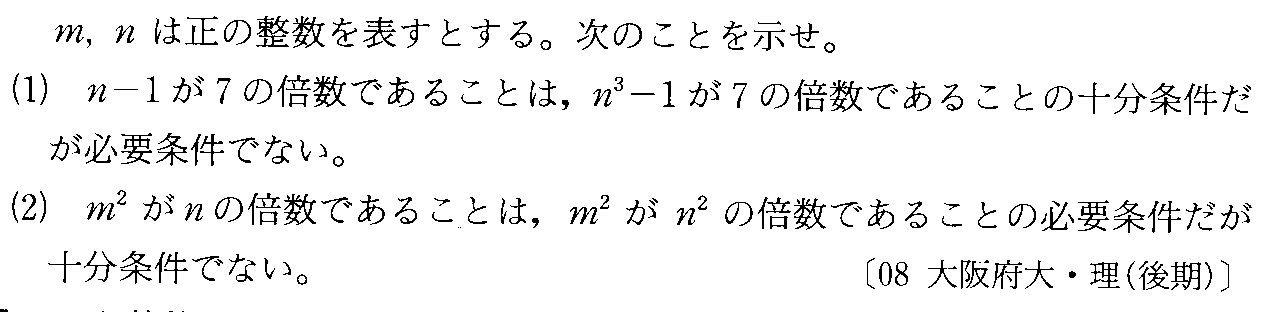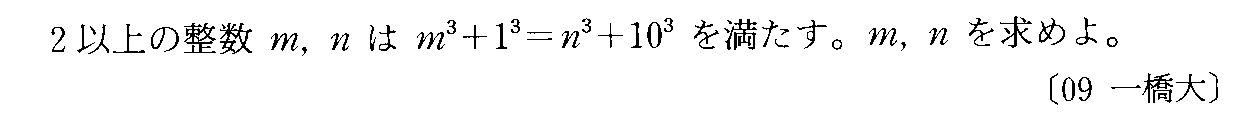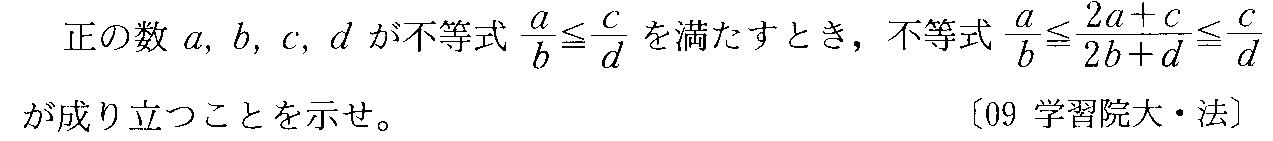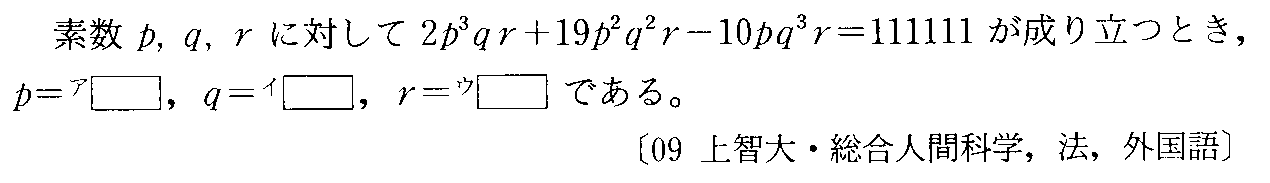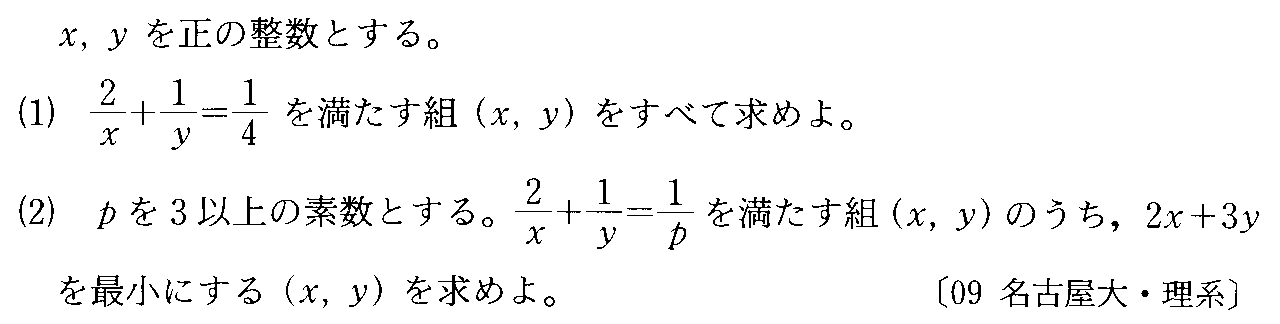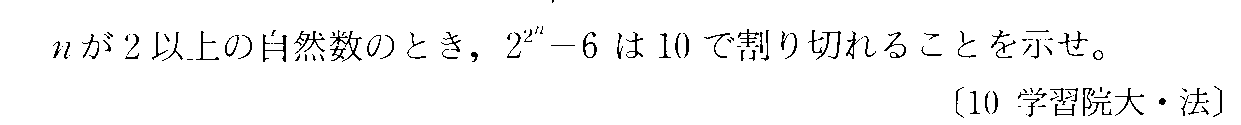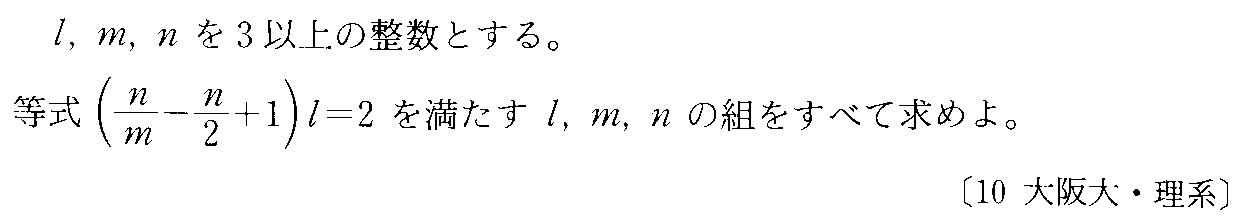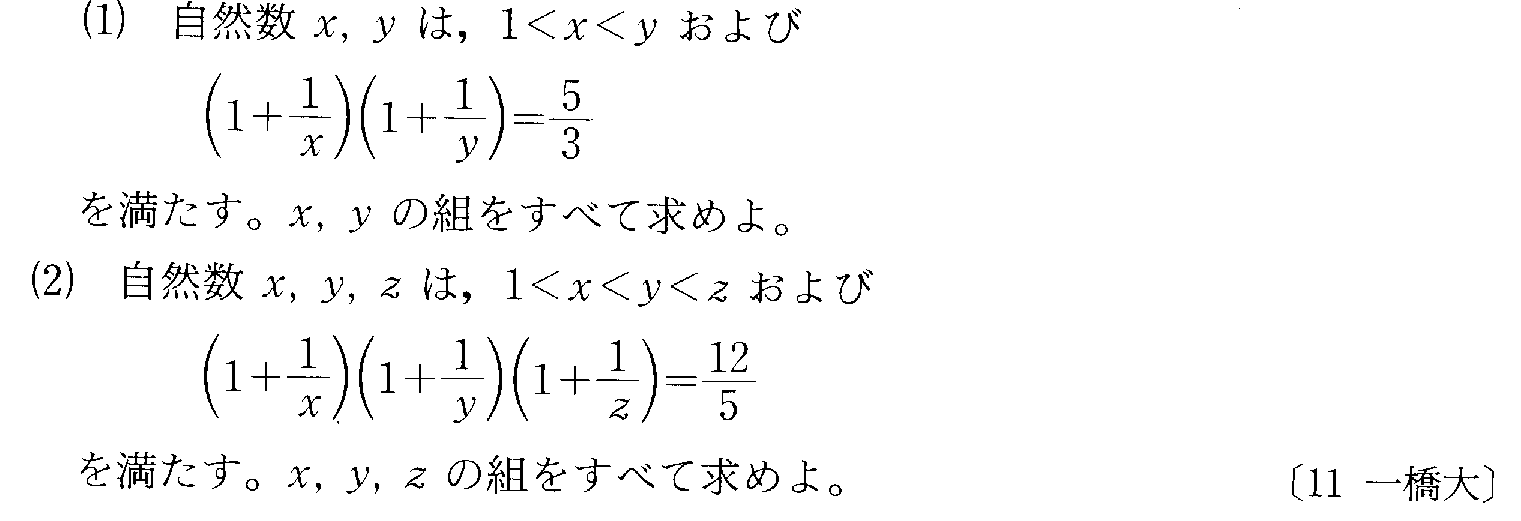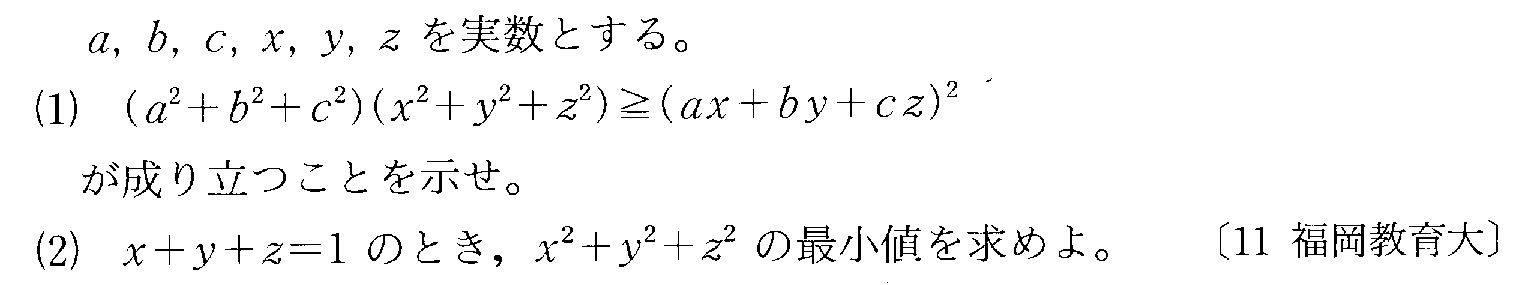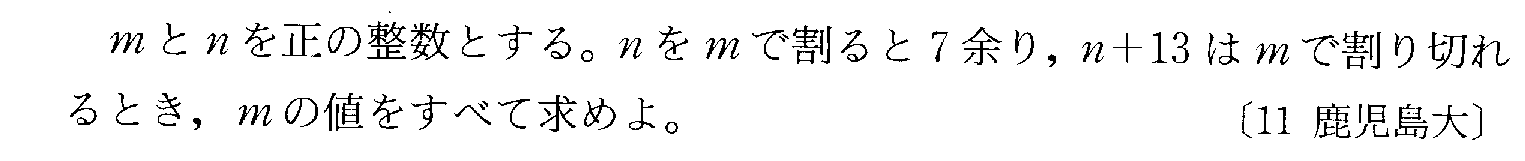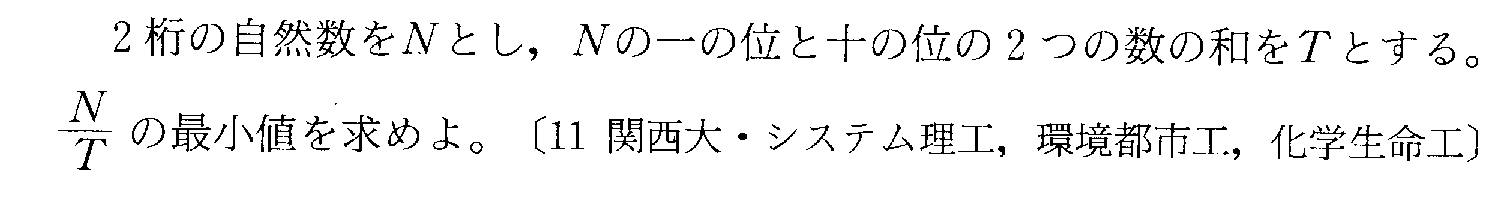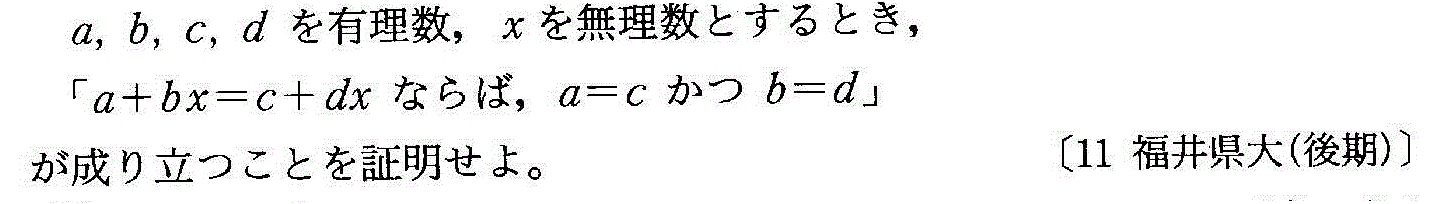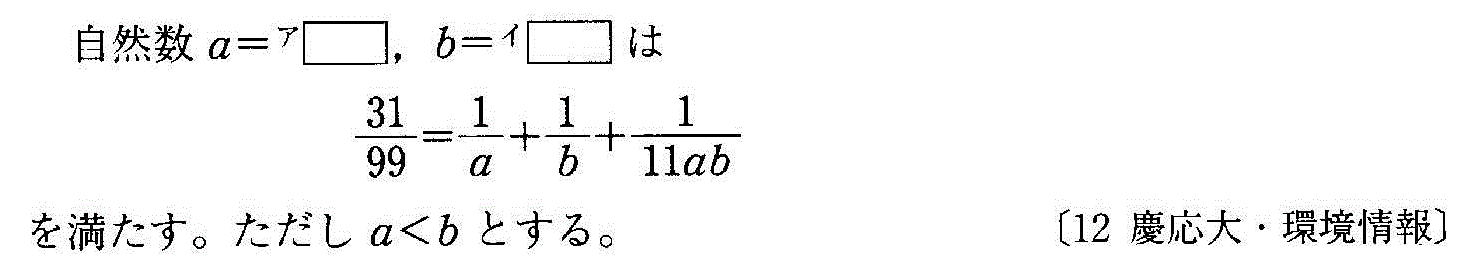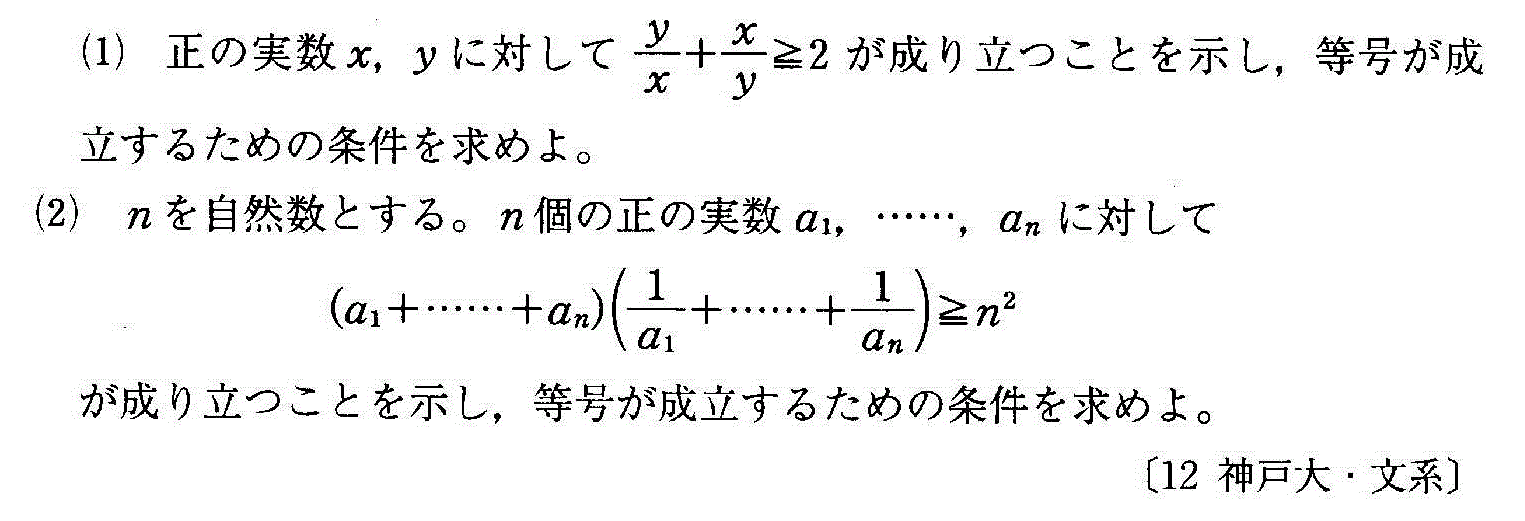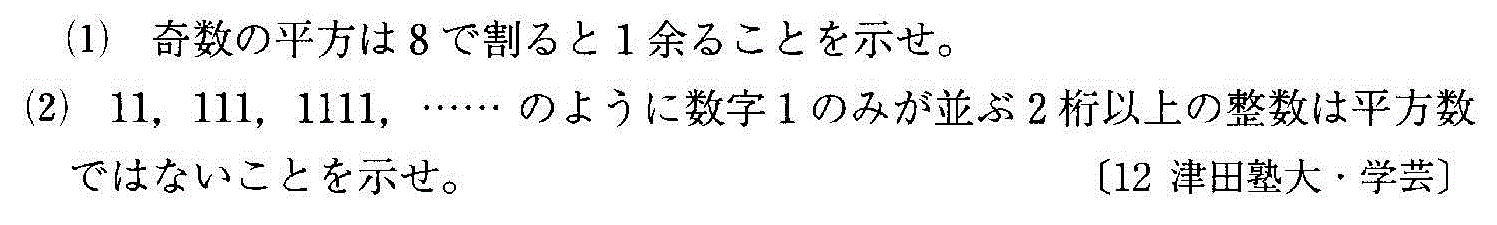- [2000b054_1]
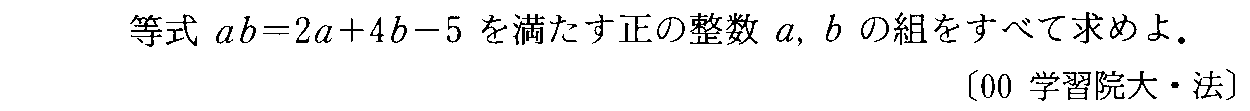
- [2000b056]
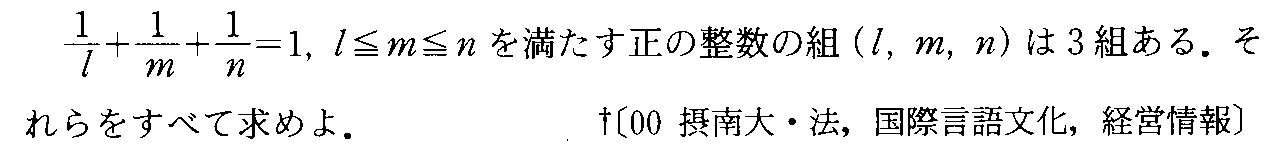
- [2000b059]

- [2000b060]
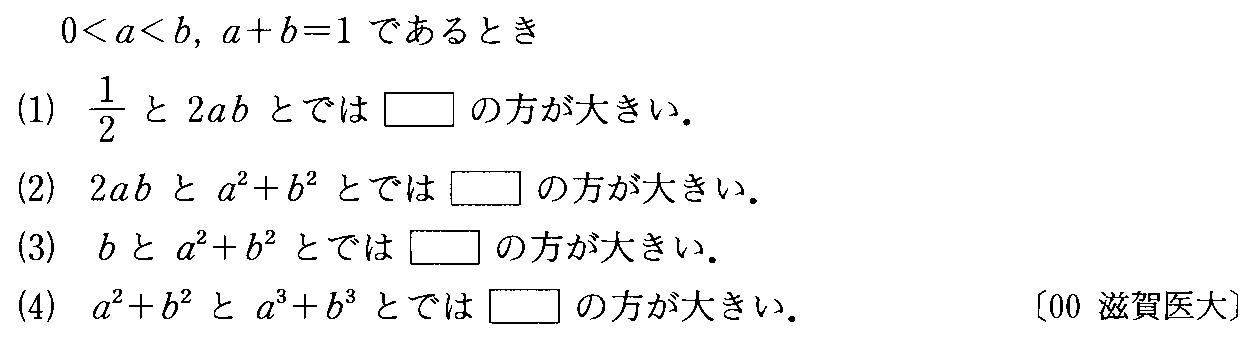
- [2000b068]

- [2000r056]

- [2000r060]

- [2000r062]
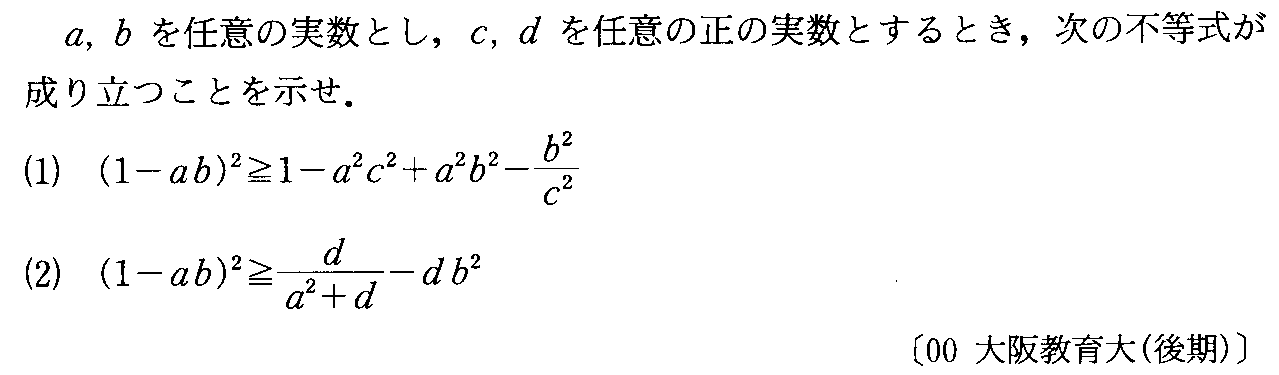
- [2000r064]

- [2000r069]
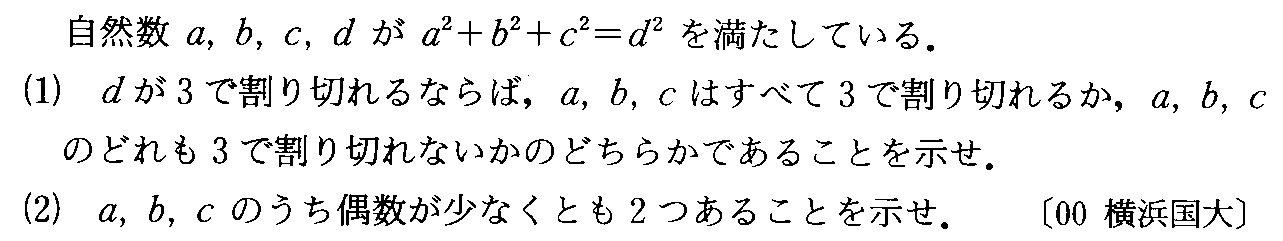
- [2000r070]*背理法

- [2000r071]
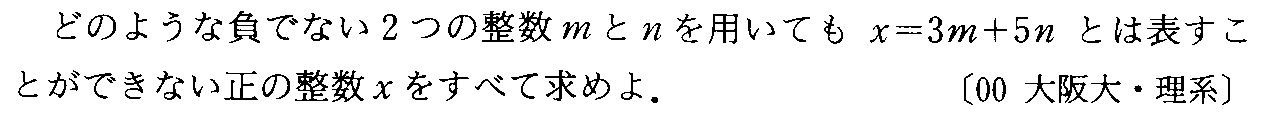
- [2000r072]
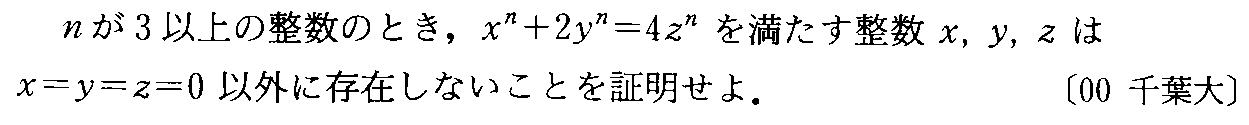
- [2000r108]

- [2001b007]

- [2001b051]

- [2001b053]

- [2001b059]

- [2001b060]*背理法

- [2001b061]

- [2001b062]

- [2001b095]

- [2001b096]*必要条件・十分条件

- [2001b097]

- [2002b017]
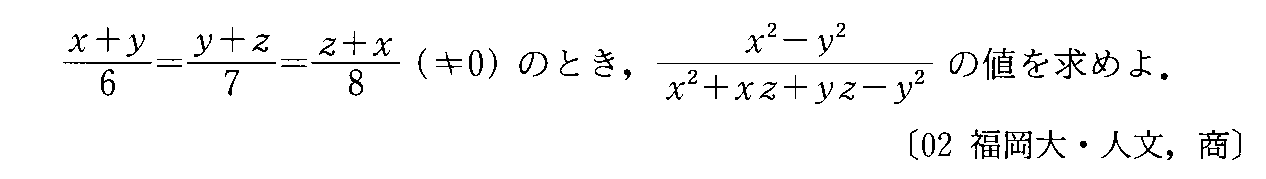
- [2002b054]

- [2002b091]

- [2002b092]

- [2002b093]

- [2002r013]
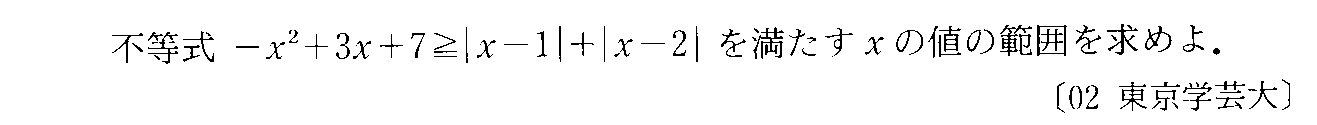
- [2002r048]
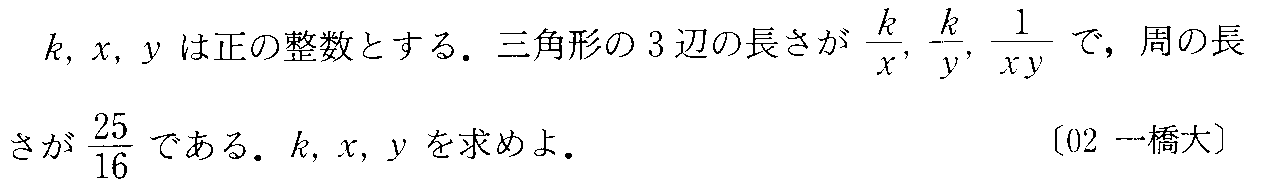
- [2002r093]

- [2002r094]*必要条件・十分条件

- [2002r095]

- [2002r096]

- [2003b035]*2次方程式の解の配置

- [2003b087]

- [2003b090]

- [2003b091]

- [2003r014]*文字係数を含む不等式

- [2003r015]

- [2003r034]*「あるexist」と「すべてall」

- [2003r046]

- [2003r052]

- [2003r055]

- [2003r057]

- [2003r059]*無理数であることの証明

- [2003r092]

- [2004b032]

- [2004b035]
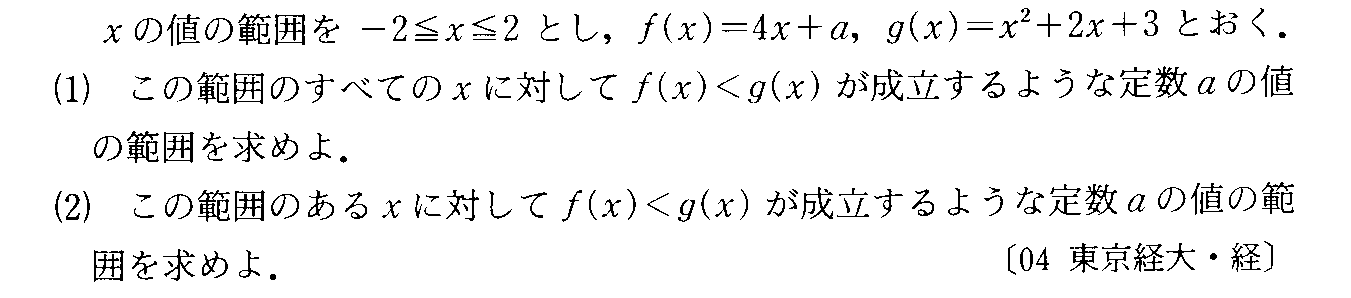
- [2004b055_1]
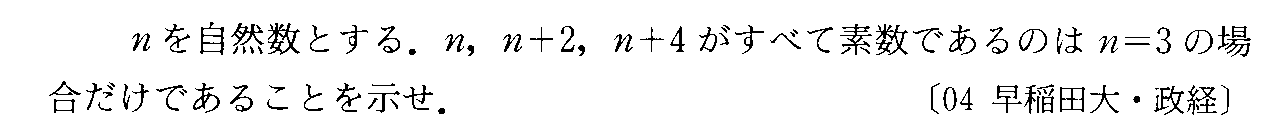
- [2004b092]

- [2004r015]

- [2004r019]

- [2004r032]*2次関数の最大最小・変数の変換

- [2004r051]

- [2004r058]*背理法・「素数」は、否定文でしか定義できない

- [2004r092]

- [2004r093]

- [2005b013]

- [2005b035]
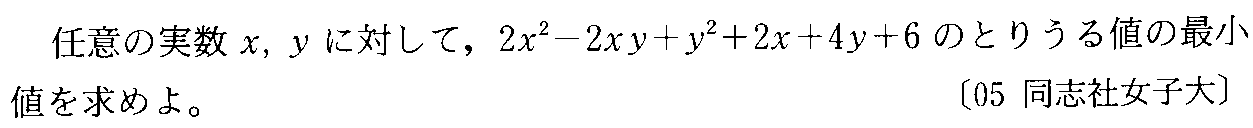
- [2005b049]*不定方程式の自然数解

- [2005b066]

- [2005b068]

- [2005b069]

- [2005r017]
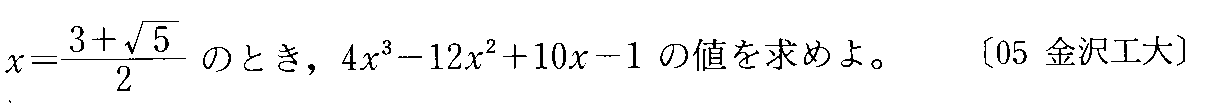
- [2005r045_2]

- [2005r066]

- [2005r067]

- [2005r068]

- [2006b009]

- [2006b015]
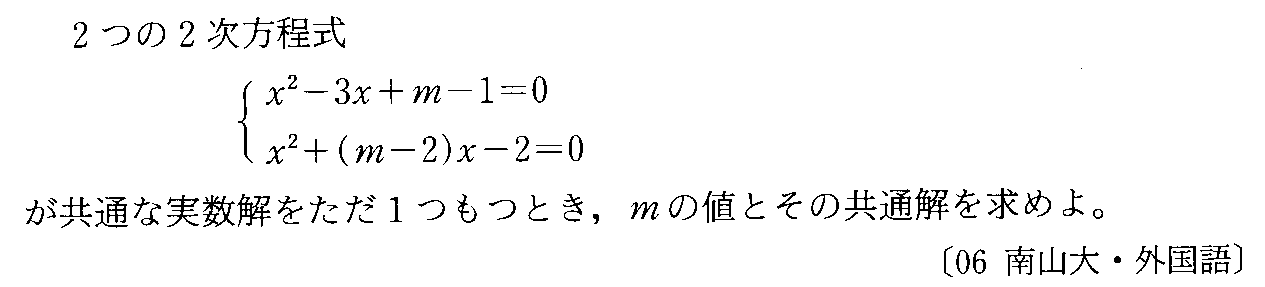
- [2006b040]

- [2006b049]

- [2006b064]

- [2006b070]

- [2006r012_1]

- [2006r063]
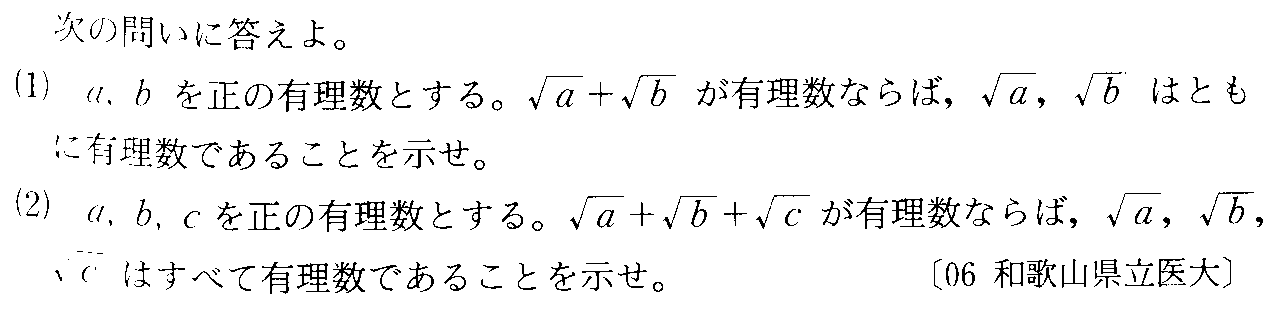
- [2006r064]*排反事象の和に分ける
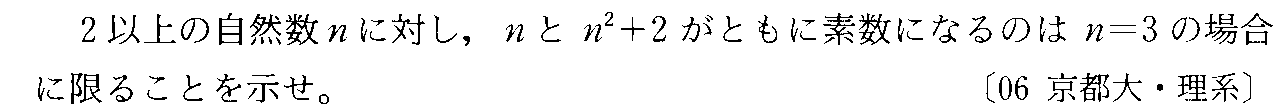
- [2006r070]

- [2006r073]
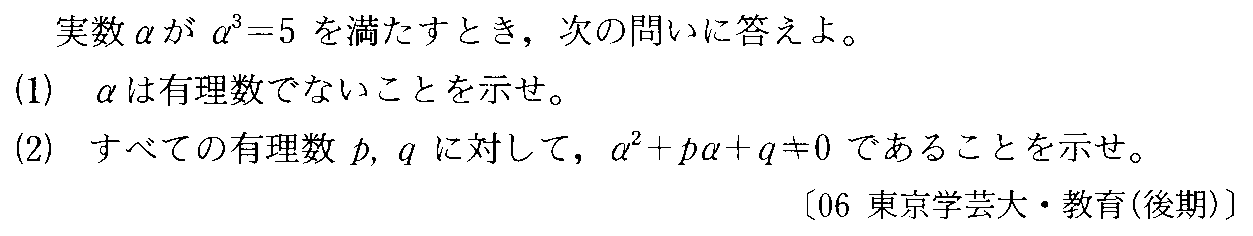
- [2007b042]

- [2007b046]
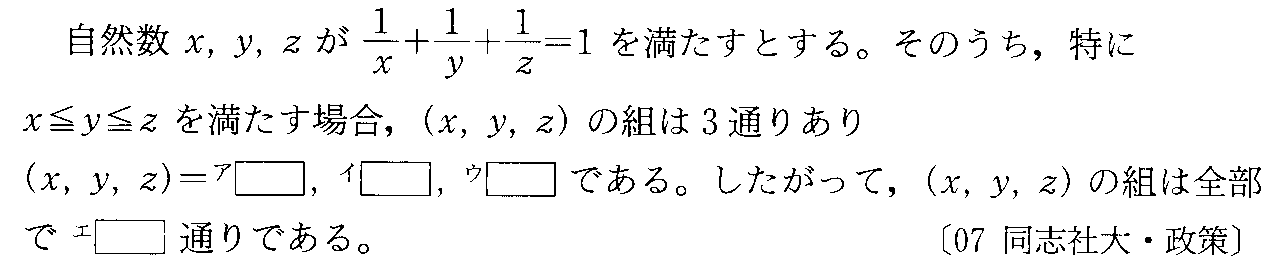
- [2007b060]

- [2007b062]

- [2007b063]

- [2007b064]

- [2007b065]

- [2007b066]

- [2007r007_2]*多項式の剰余
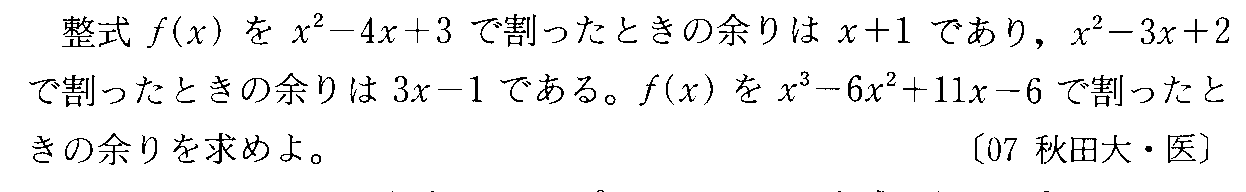
- [2007r017_2]
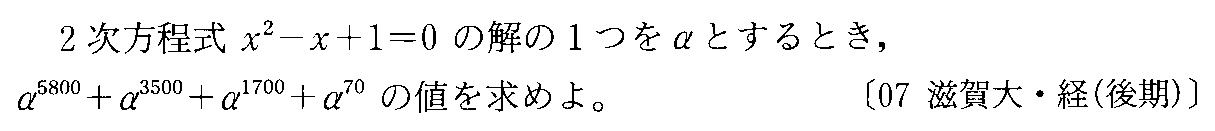
- [2007r035]
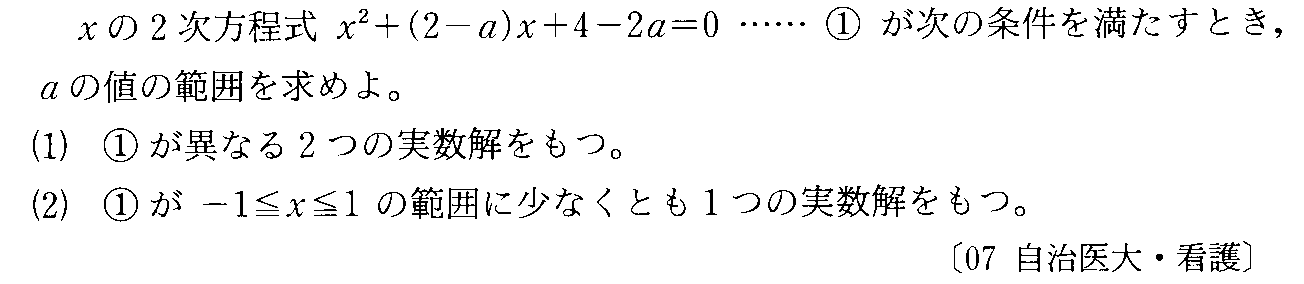
- [2007r058]
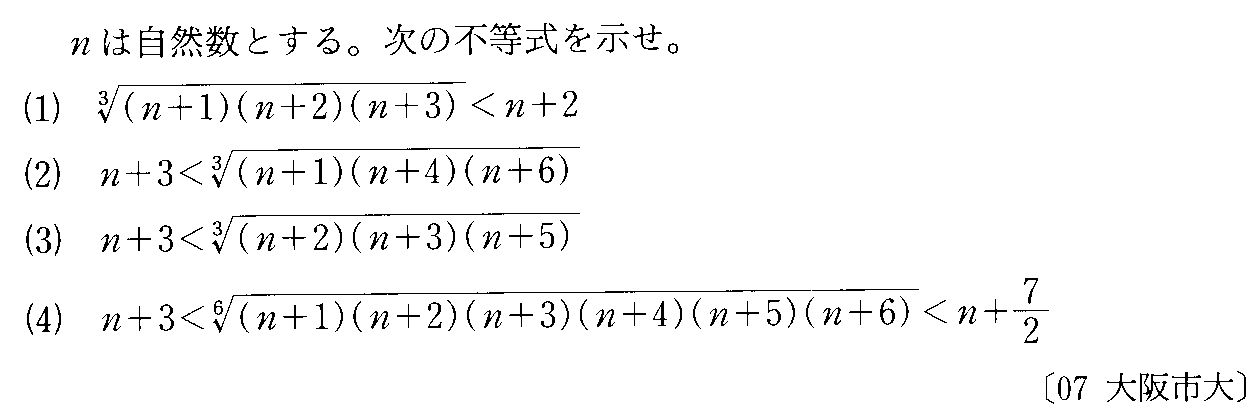
- [2007r060]

- [2007r061]

- [2007r062]

- [2007r066]*必要条件・十分条件

- [2007r067]

- [2008b016_2]
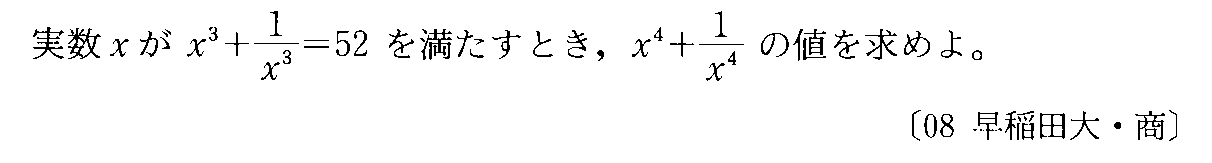
- [2008b018]
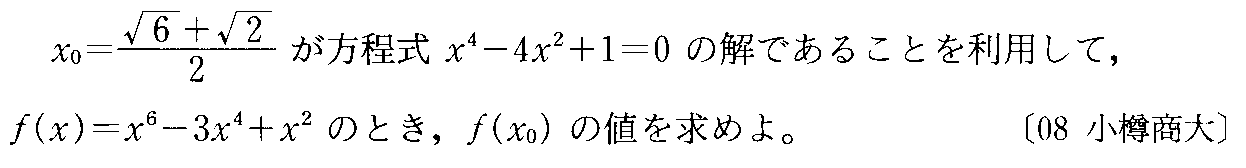
- [2008b041]

- [2008b042]
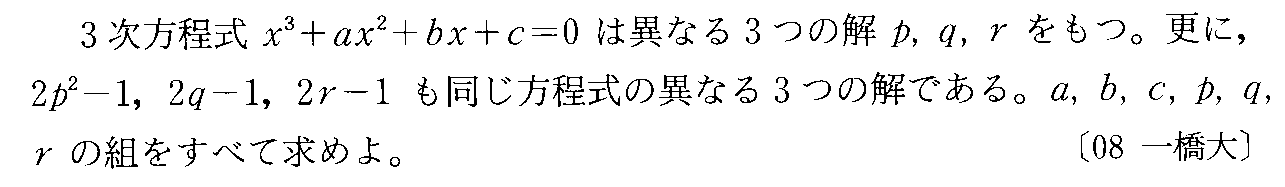
- [2008b043]
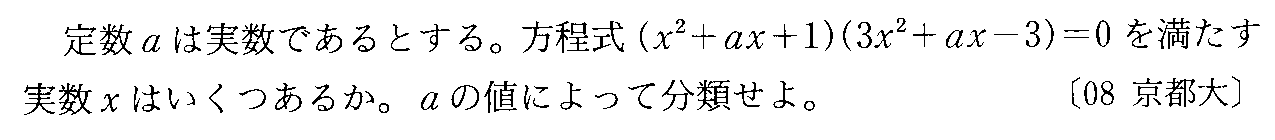
- [2008b052]
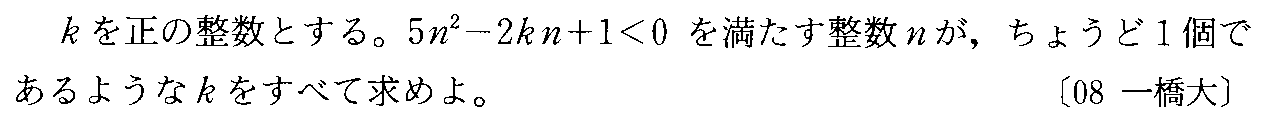
- [2008b059]

- [2008b060]

- [2008b061]
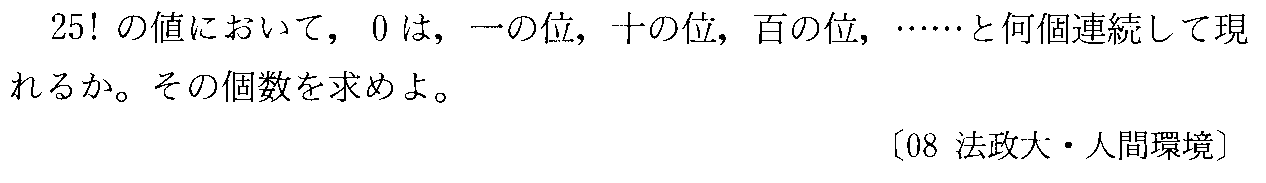
- [2008b062]
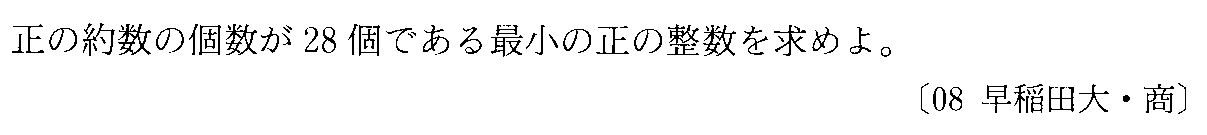
- [2008b063]

- [2008b065]*集合の演算

- [2008b067]
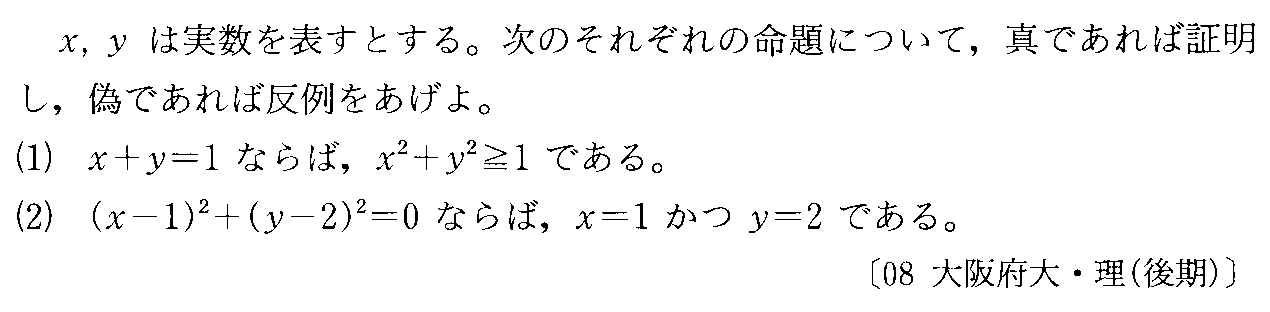
- [2008b068]

- [2008b069]

- [2008r016]

- [2008r042]

- [2008r043]

- [2008r046_2]*複素数の相等

- [2008r049]

- [2008r054]
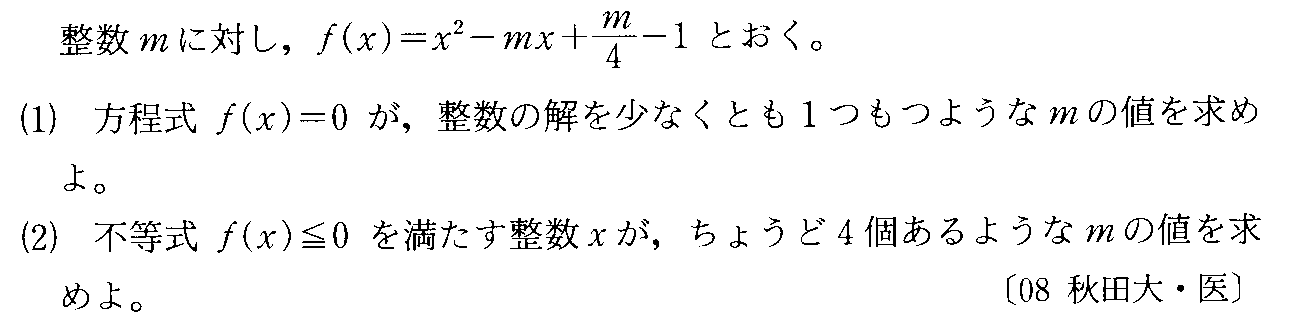
- [2008r060]*不等式の証明・等号成立の条件
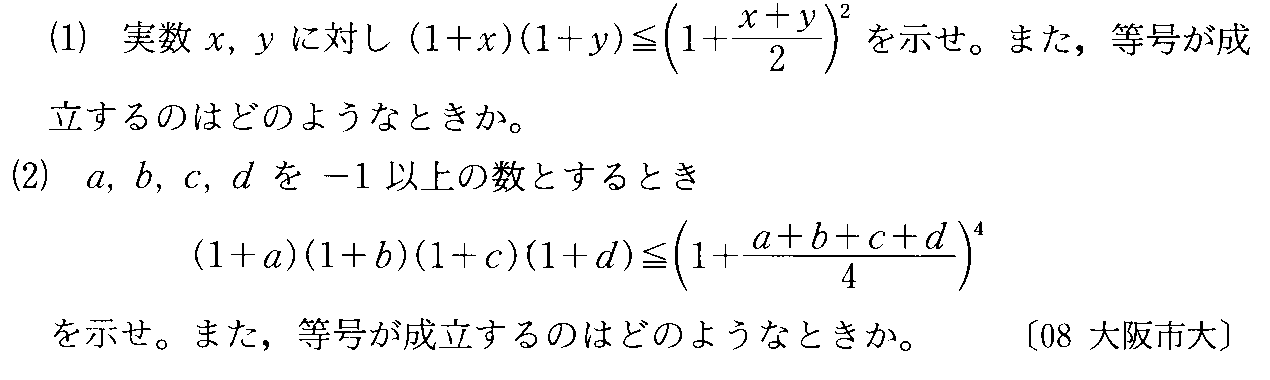
- [2008r062]

- [2008r063]

- [2008r067]

- [2008r068]

- [2008r069]

- [2008r070]
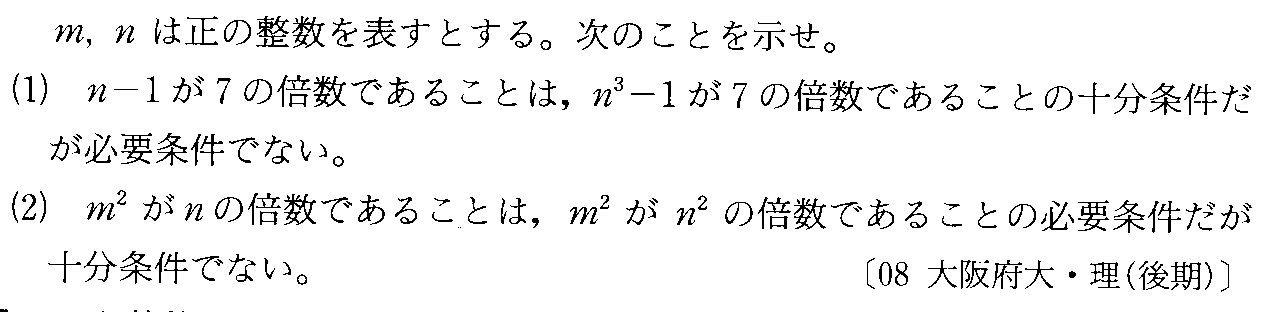
- [2009b009]

- [2009b041]

- [2009b043]*不定方程式の整数解

- [2009b045]
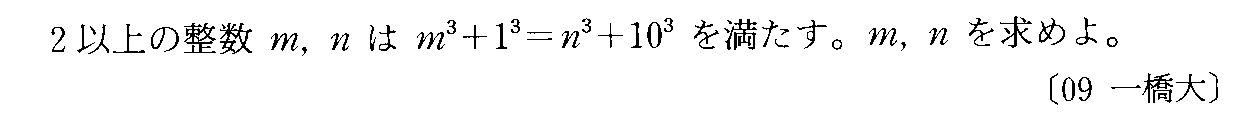
- [2009b054]

- [2009b055]
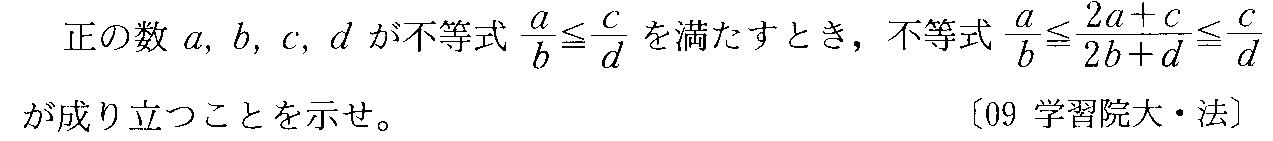
- [2009b056]

- [2009b057]

- [2009b061]
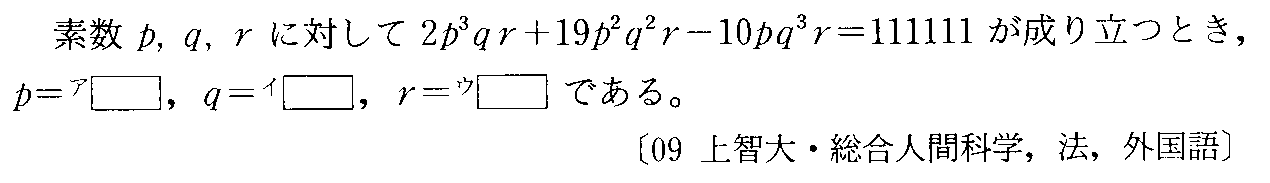
- [2009b063]

- [2009b064]

- [2009b065]*必要条件・十分条件

- [2009b067]

- [2009b068]

- [2009b069]

- [2009r016_4]

- [2009r020]

- [2009r023]

- [2009r040]

- [2009r041]

- [2009r044]
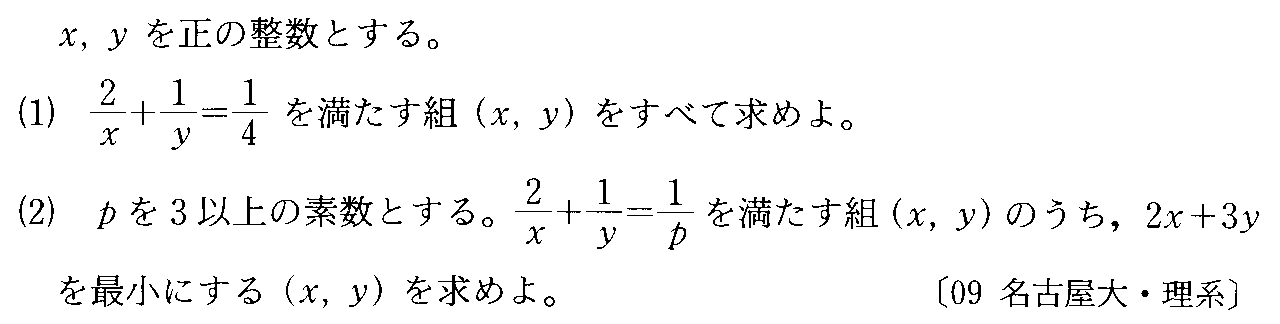
- [2009r046]

- [2009r047]
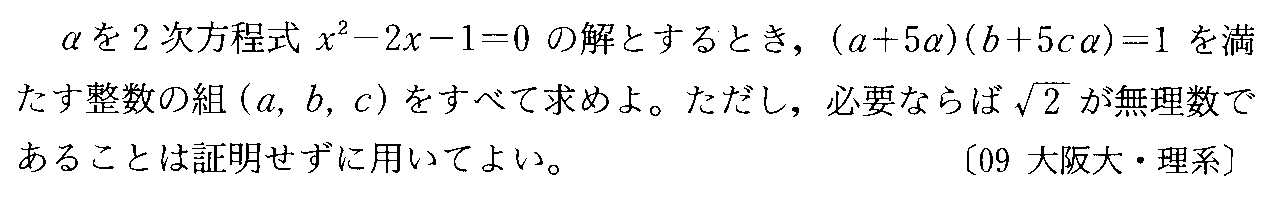
- [2009r050]

- [2009r051]

- [2009r061]

- [2009r066]

- [2009r067]
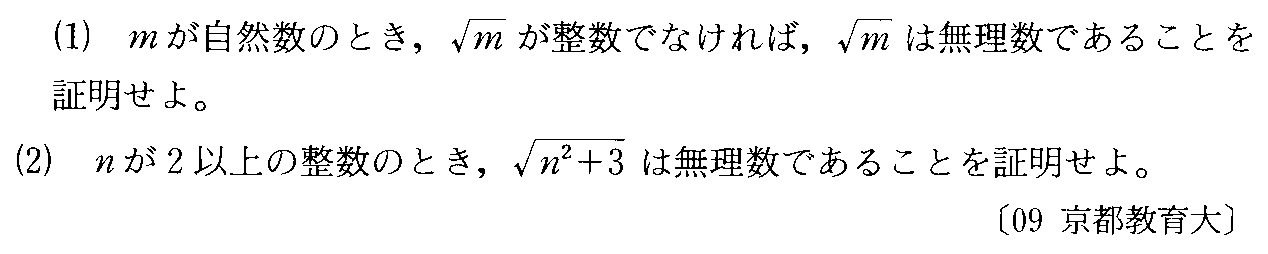
- [2010b028]

- [2010b039]

- [2010b043]

- [2010b046]

- [2010b060]
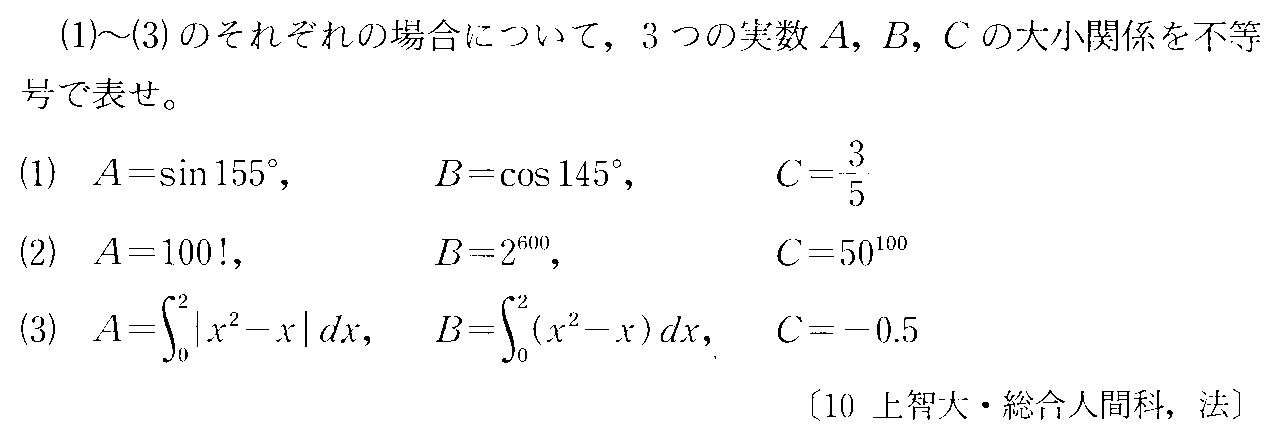
- [2010b062]*背理法

- [2010b063]

- [2010b064]
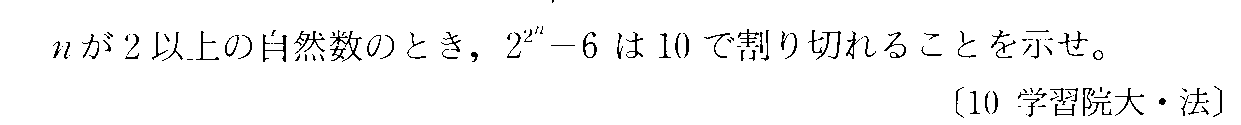
- [2010b068]

- [2010r031]

- [2010r046]
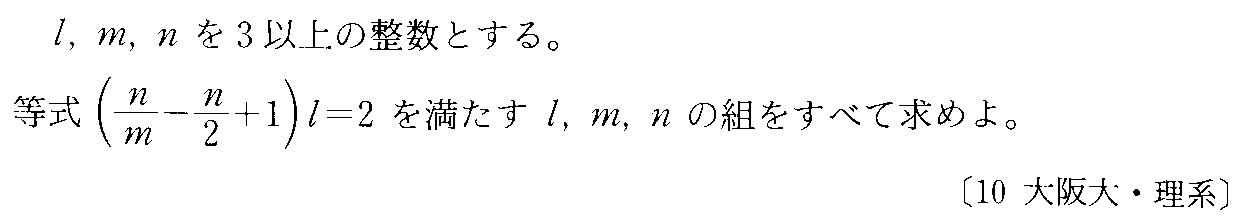
- [2010r064]

- [2010r065]

- [2010r070]

- [2011b026]

- [2011b047]
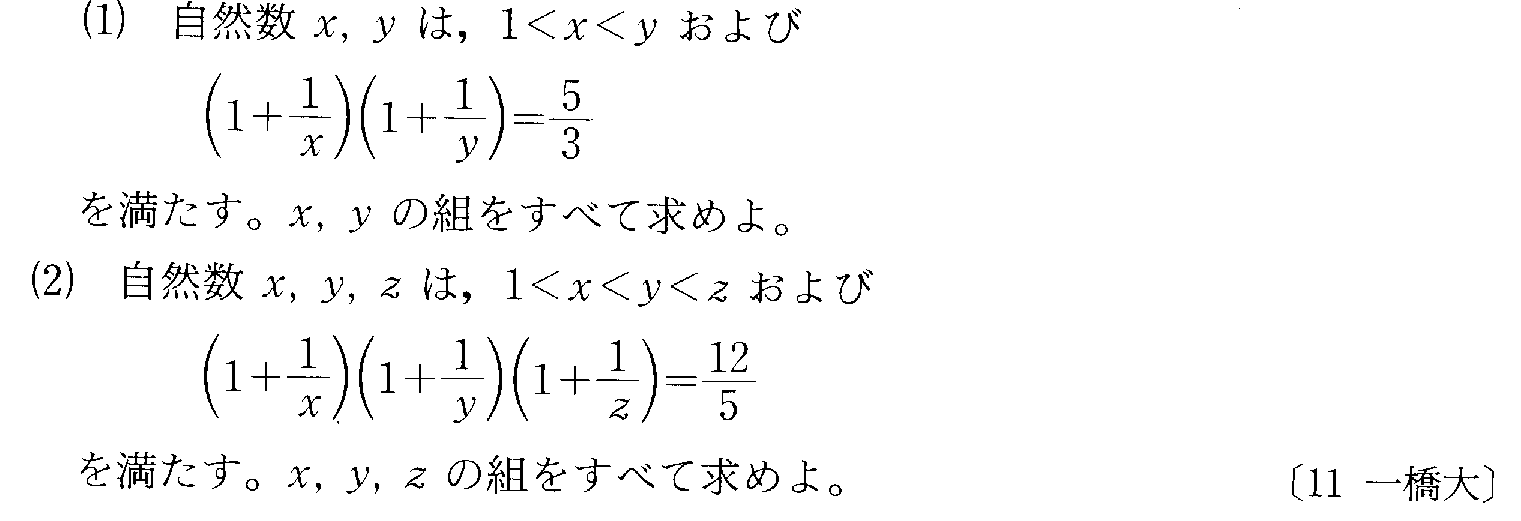
- [2011b056]

- [2011b057]*不等式の証明
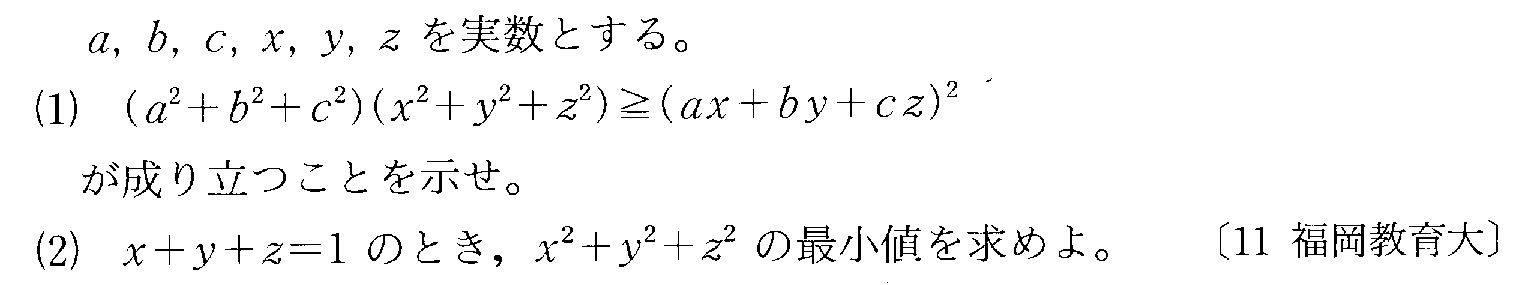
- [2011b060]

- [2011b061_1]

- [2011b061_2]
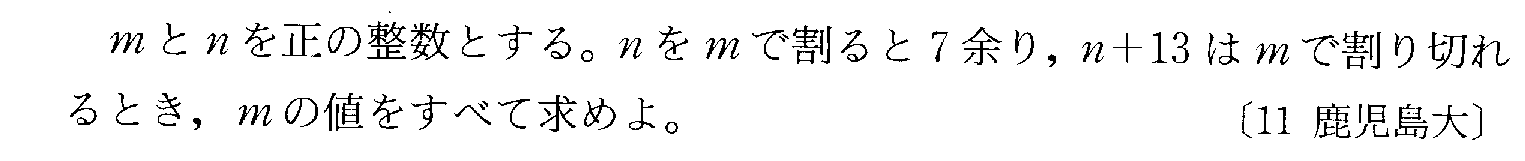
- [2011b061_3]
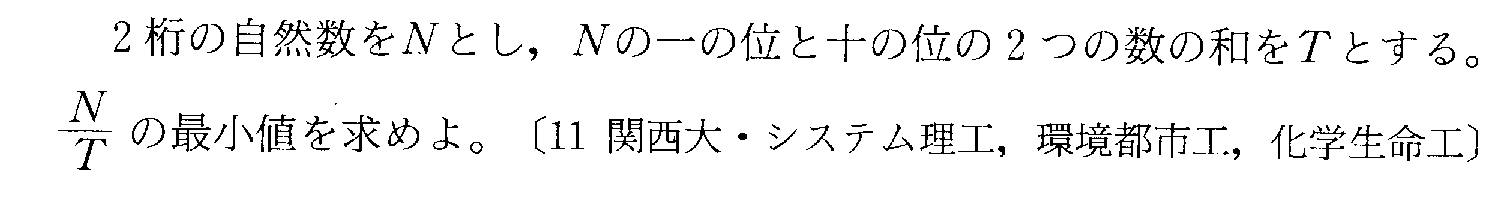
- [2011b062]

- [2011b065]

- [2011b066_1]

- [2011b066_2]
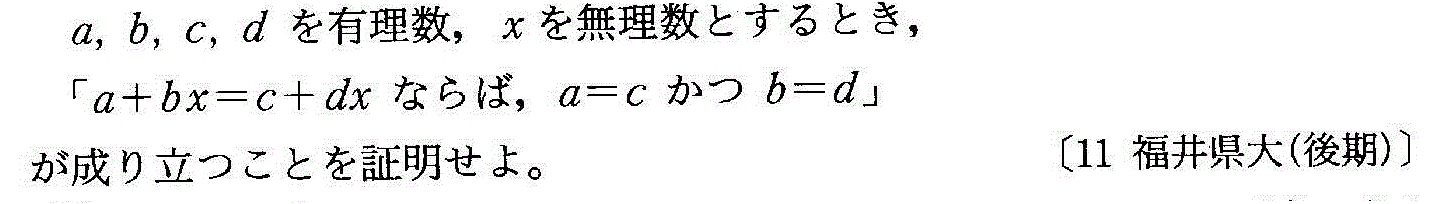
- [2011b068]

- [2011r065]

- [2011r066_2]

- [2011r067_1]

- [2012b046]
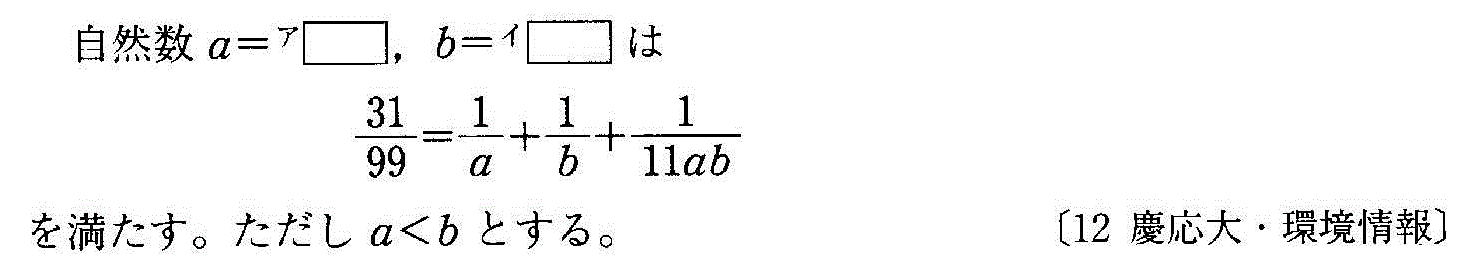
- [2012b054]*相加平均相乗平均
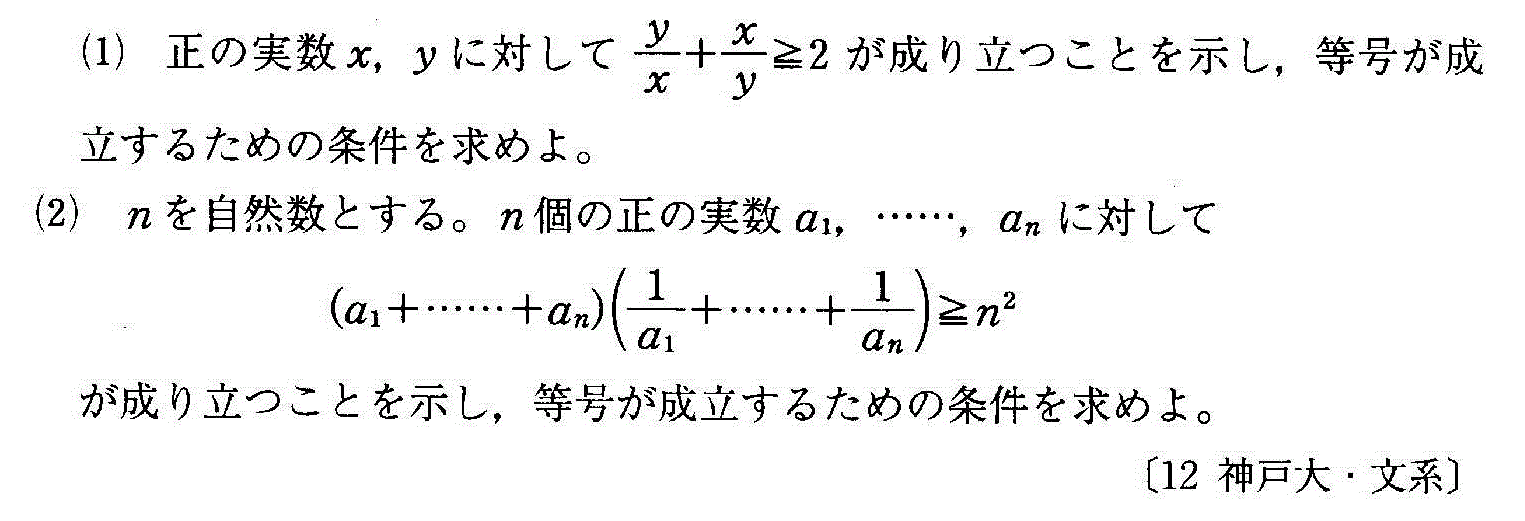
- [2012b059]*不定方程式の整数解・剰余系による分類

- [2012r017_2]

- [2012r048]

- [2012r058]
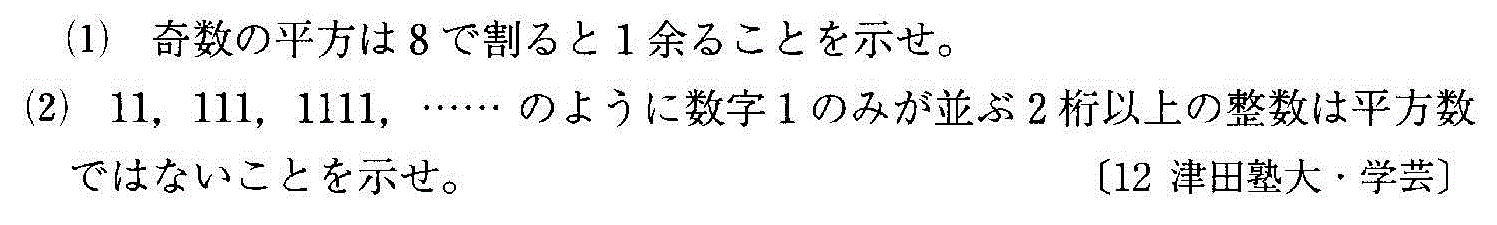
- [2012r061]

- [2012r063]

- [2012r068]

- [2012r069]