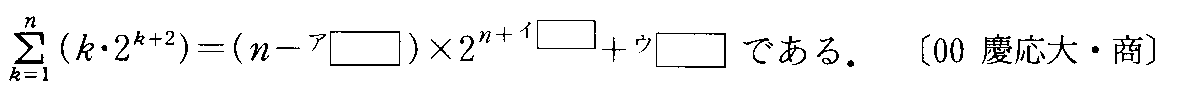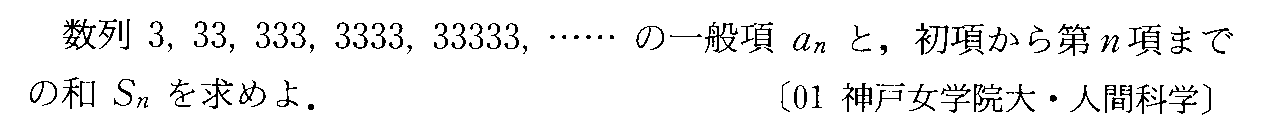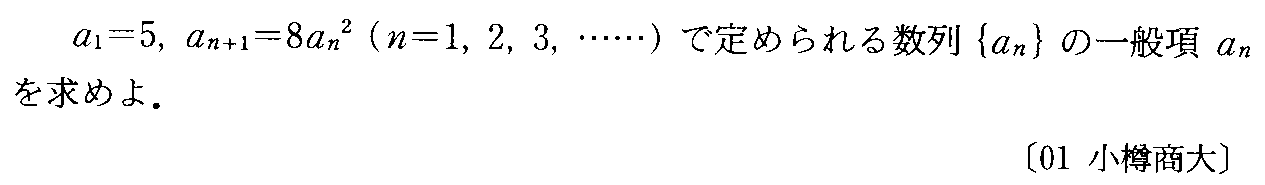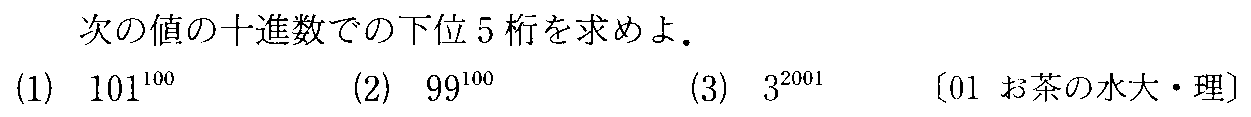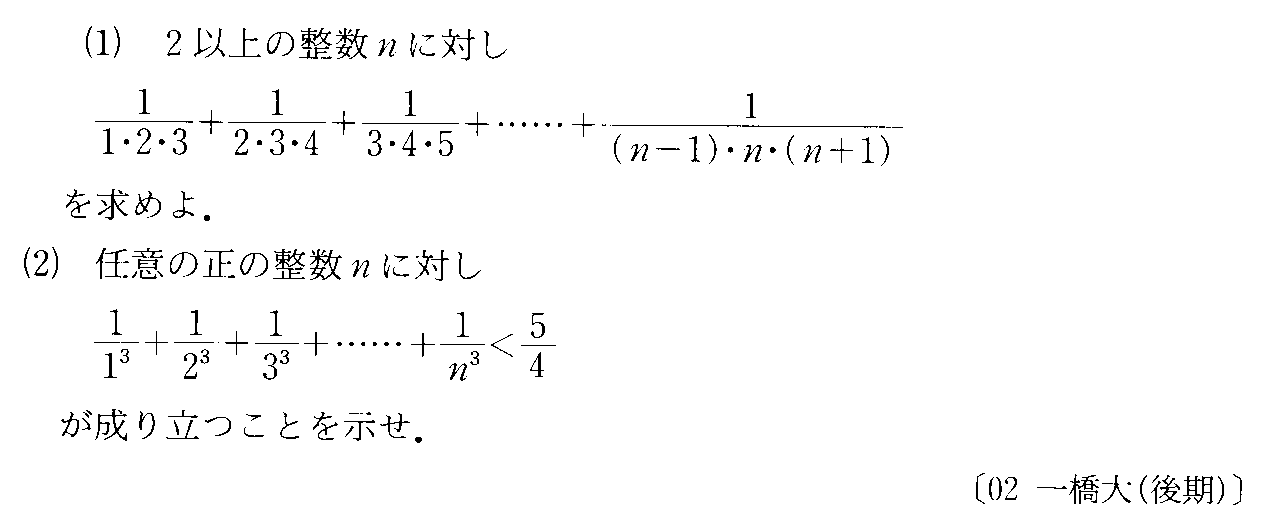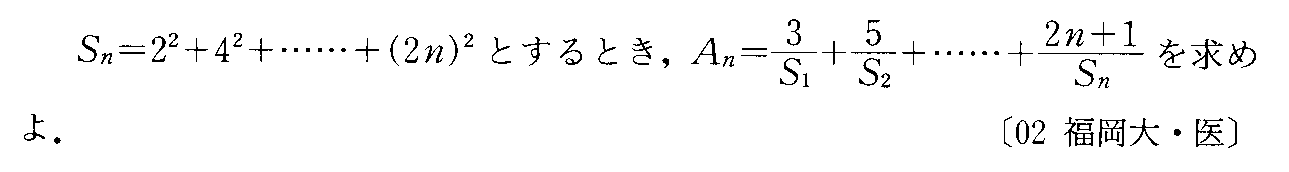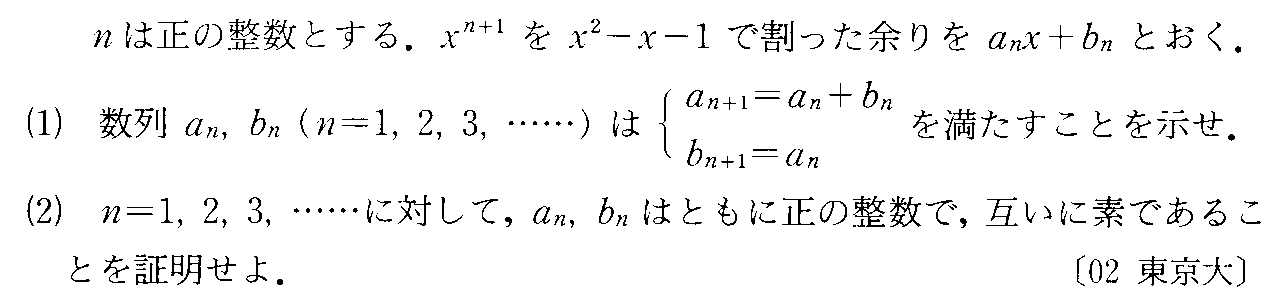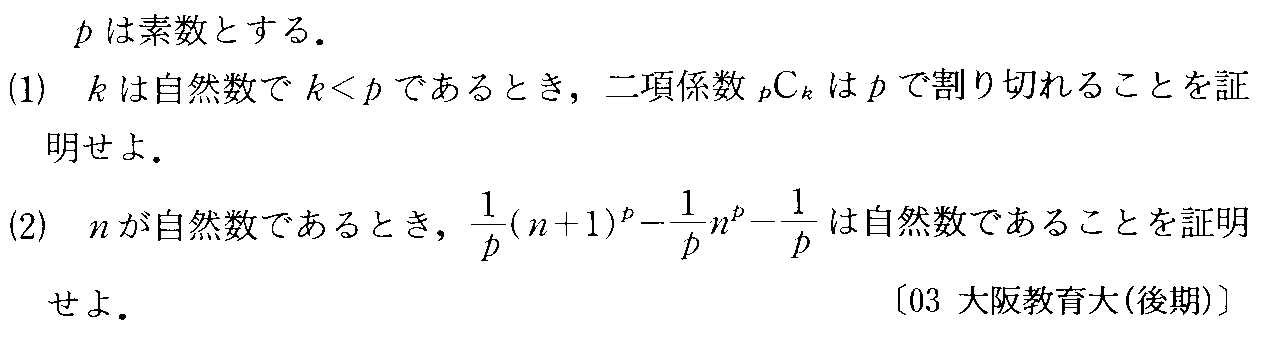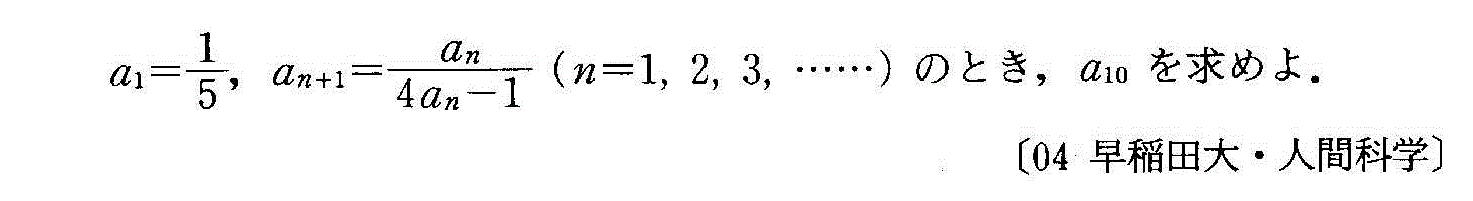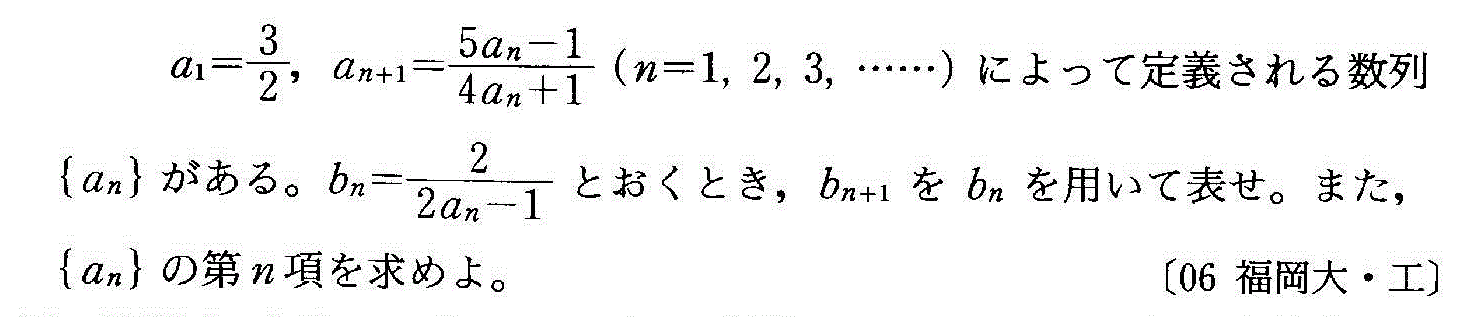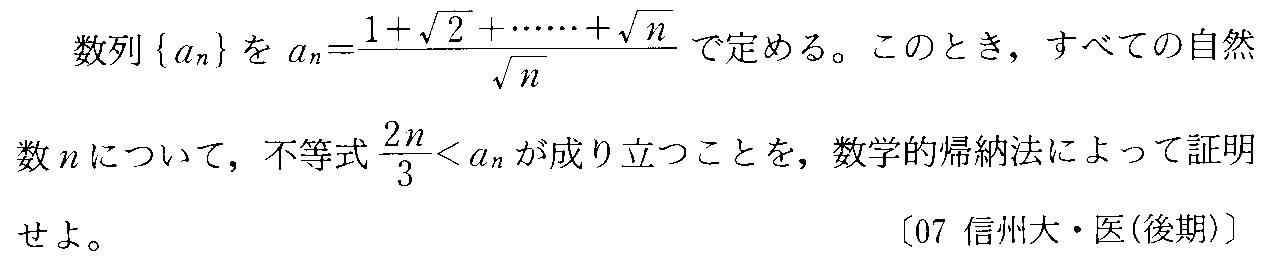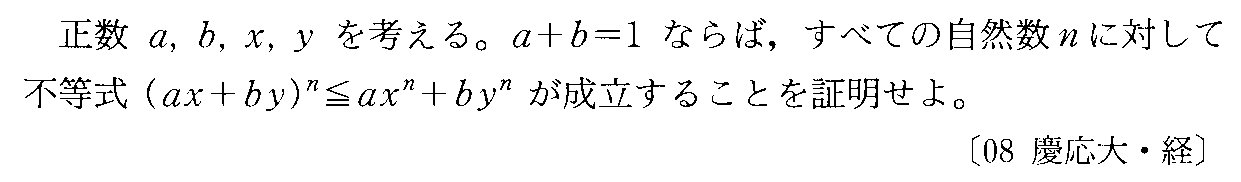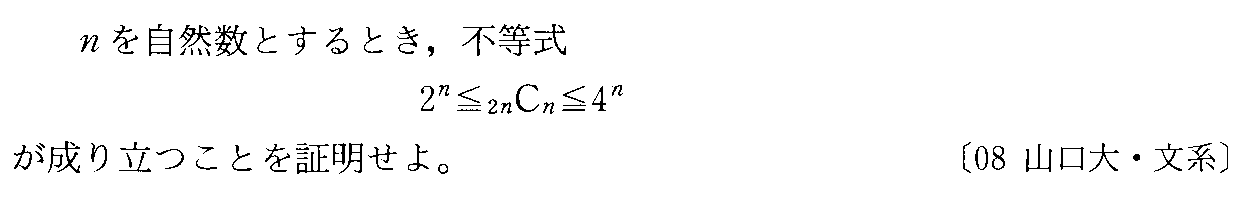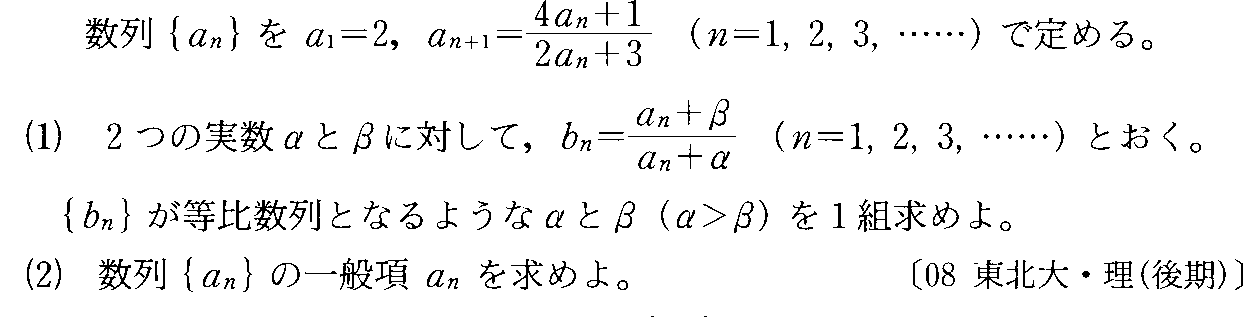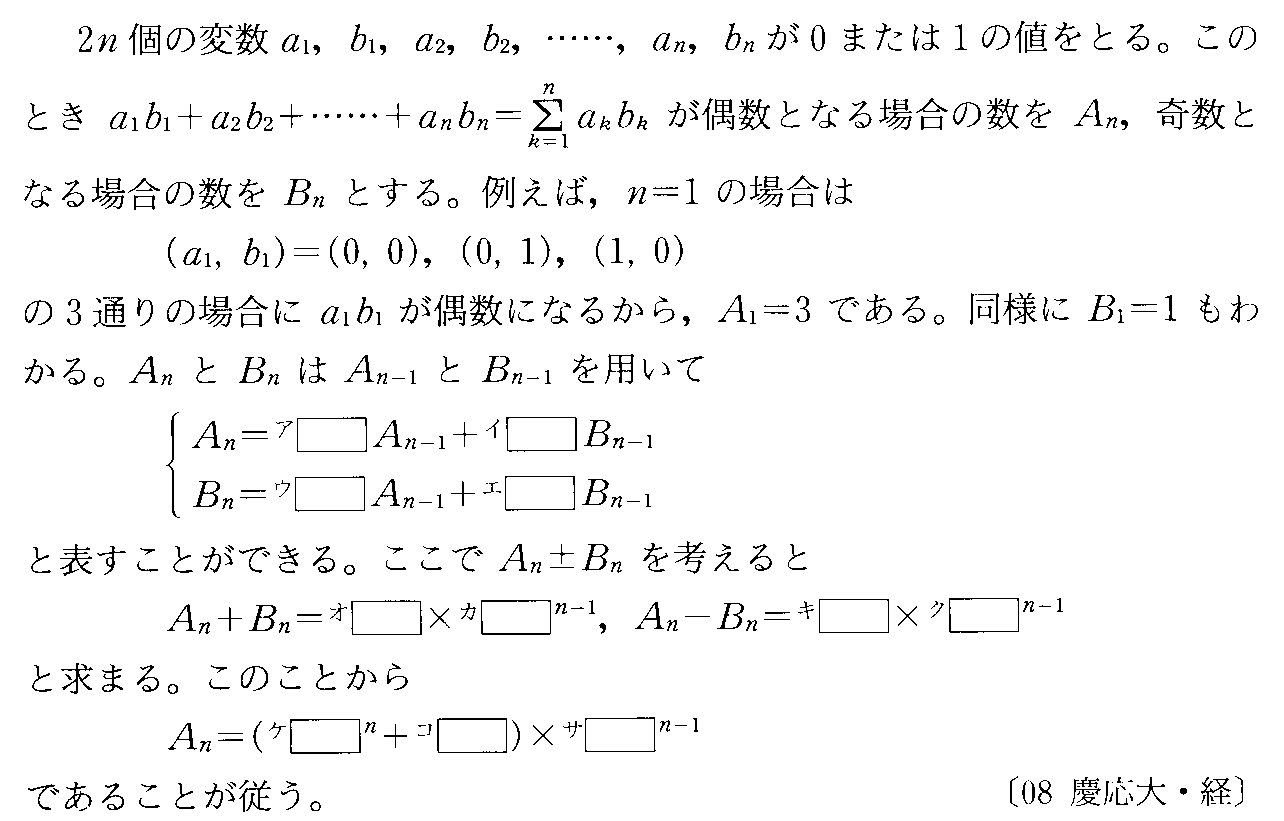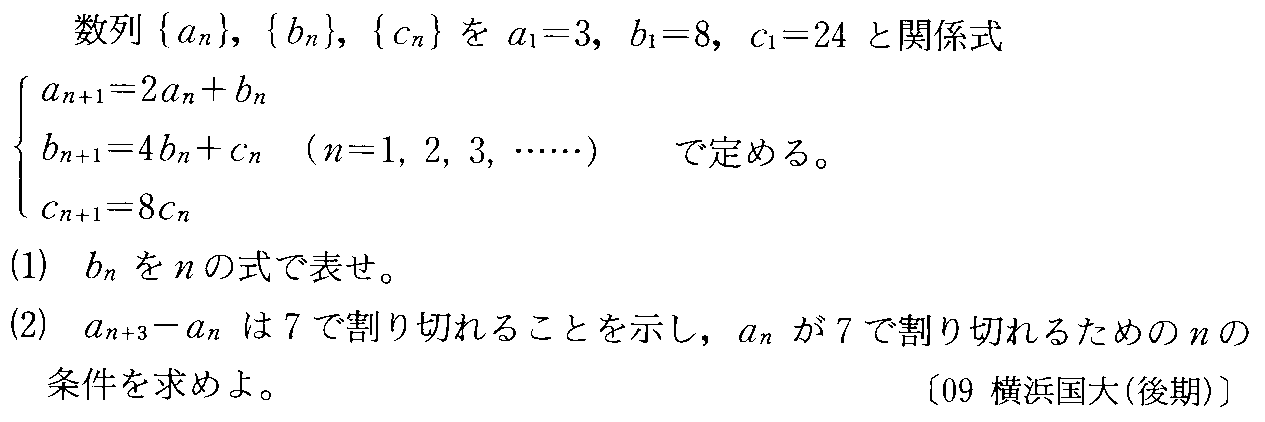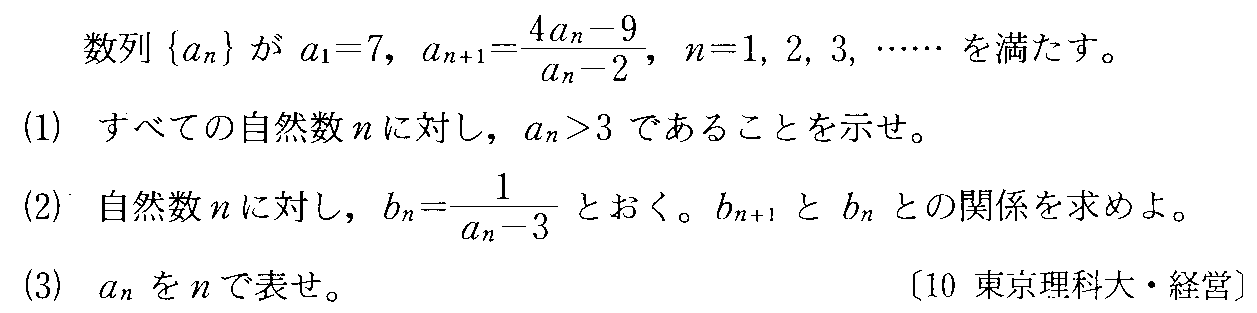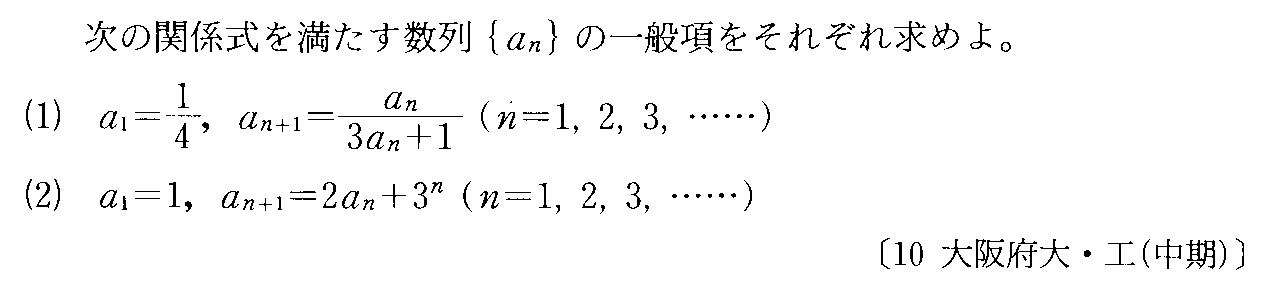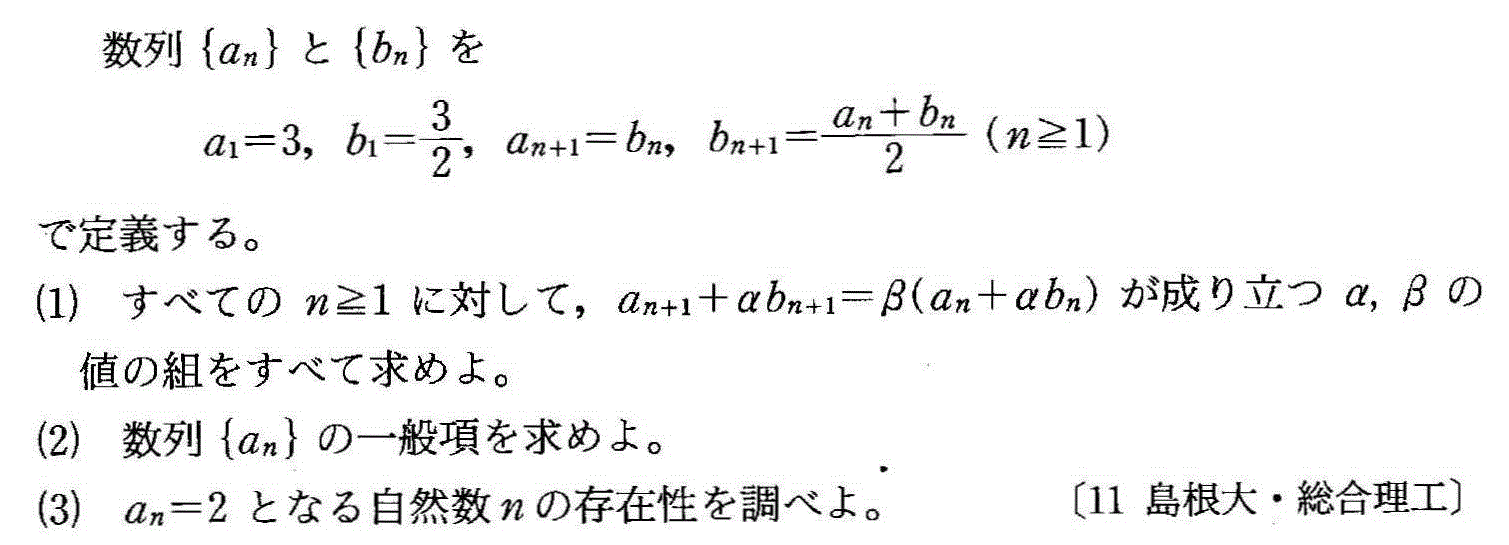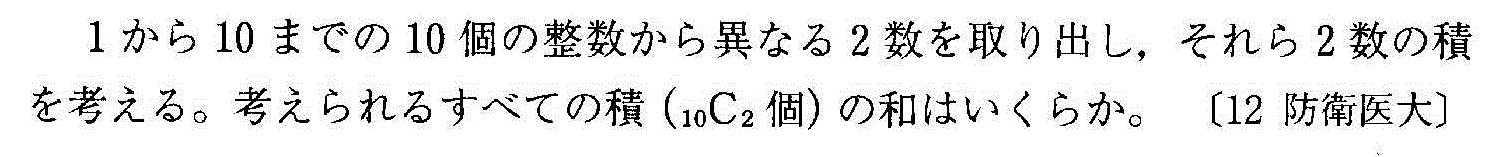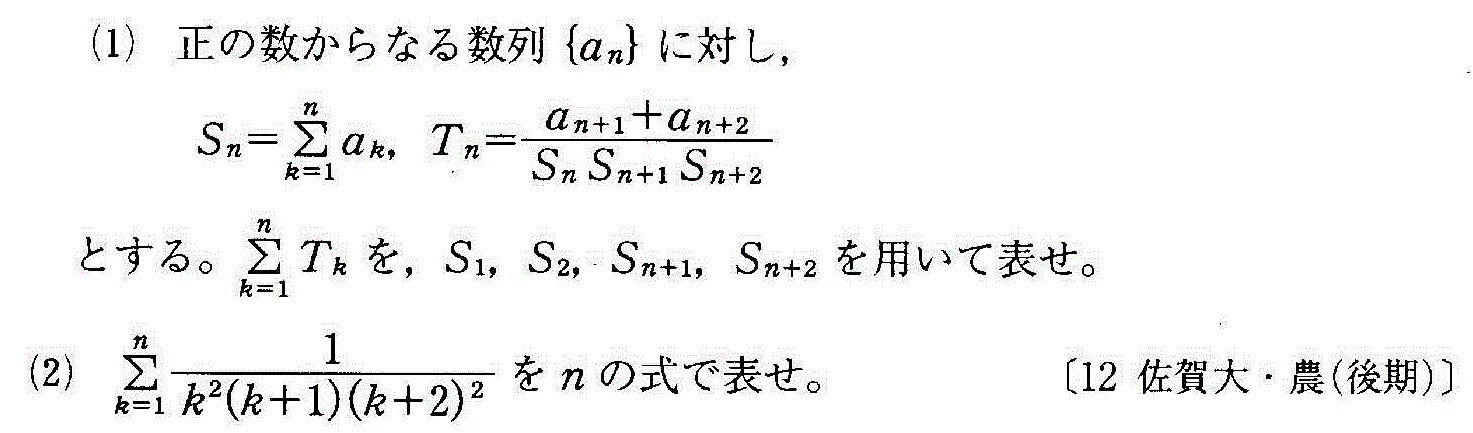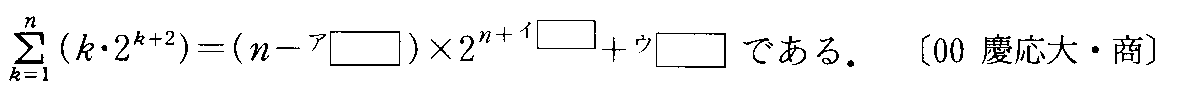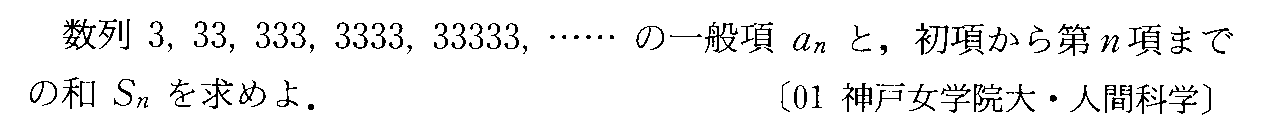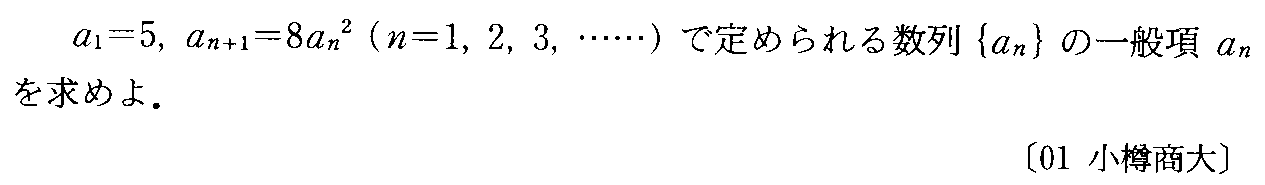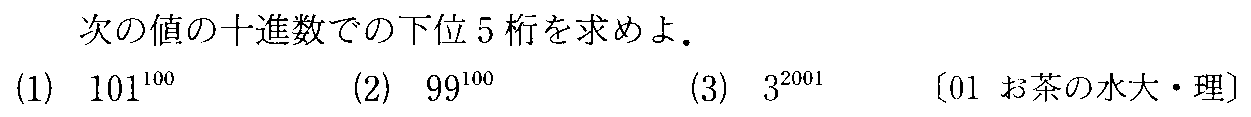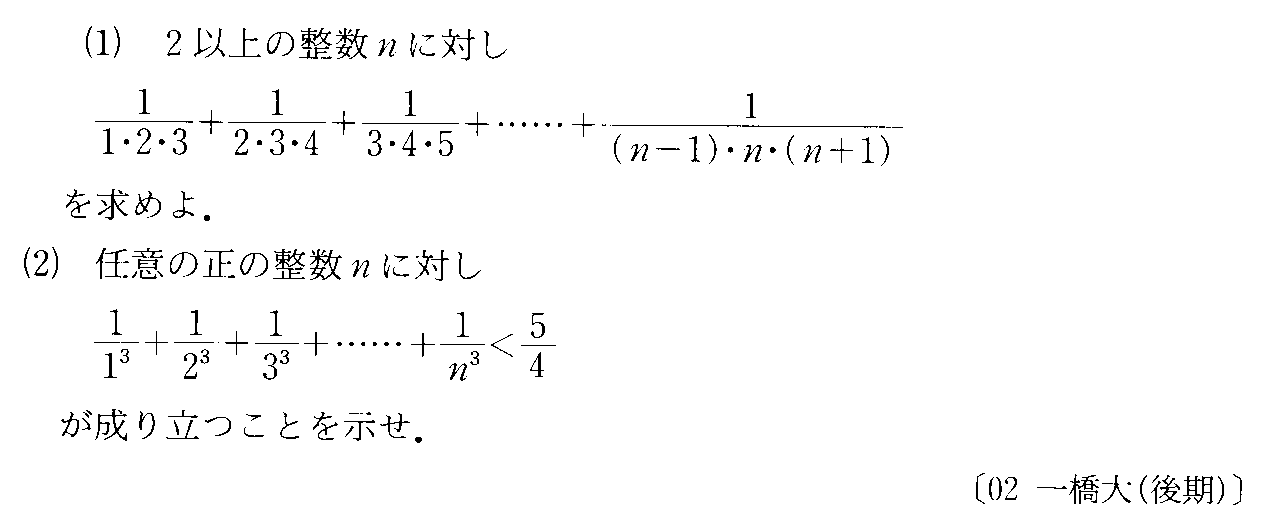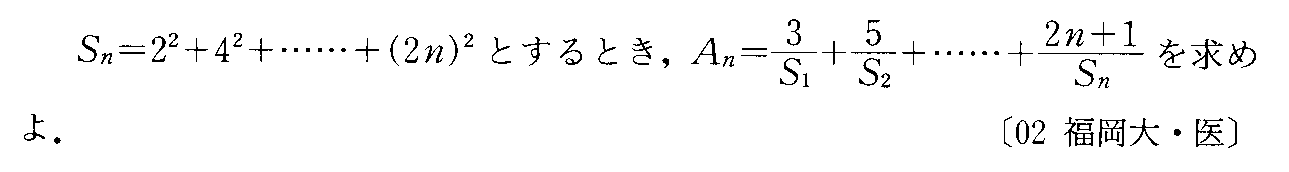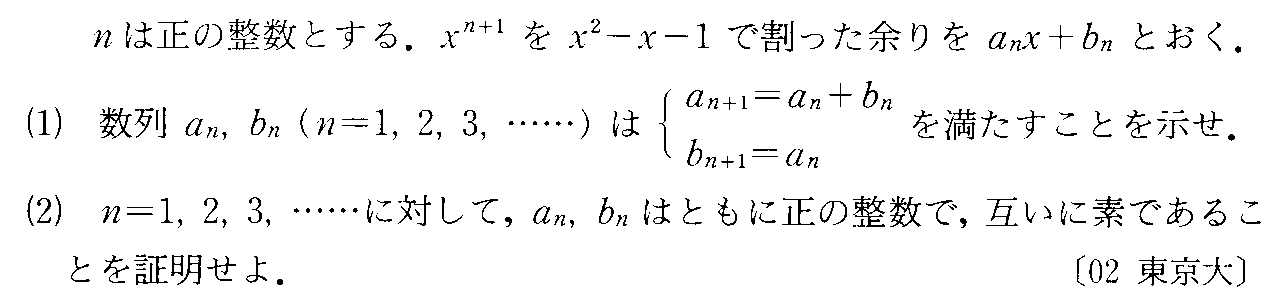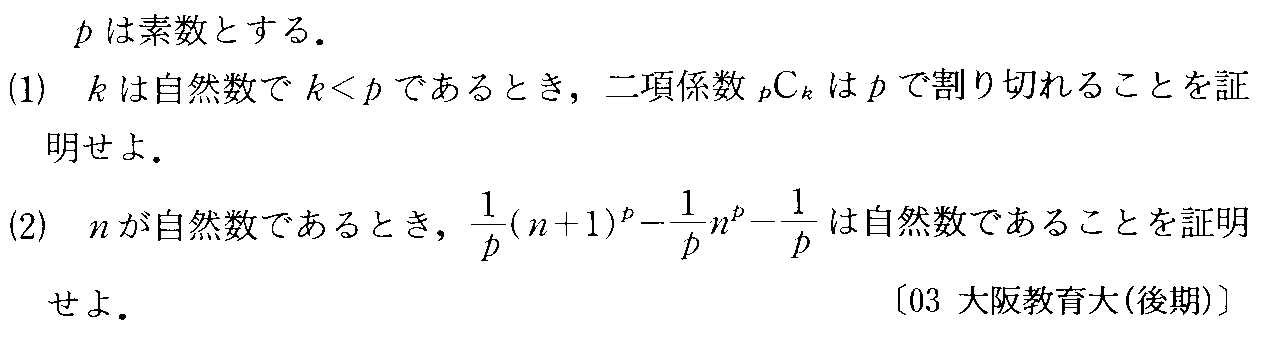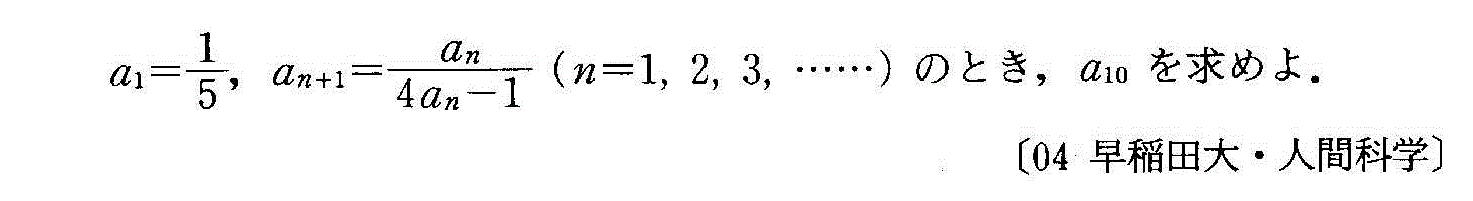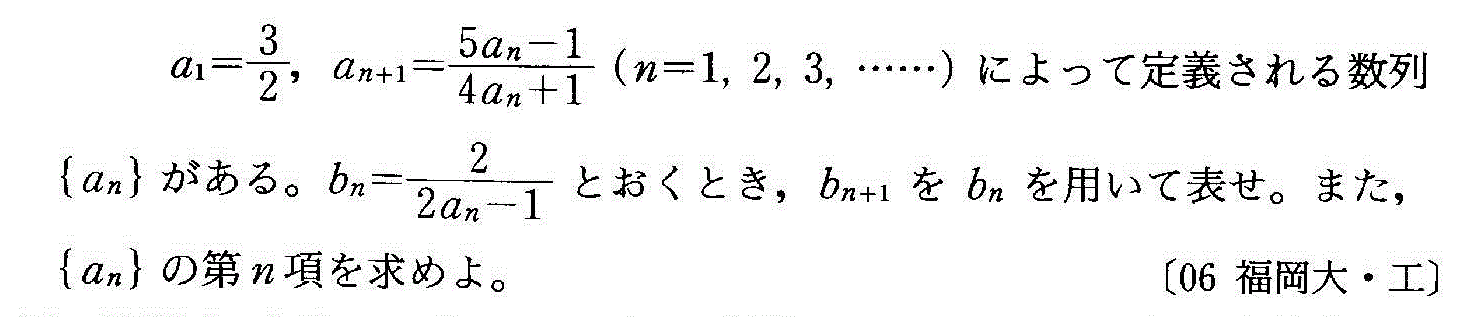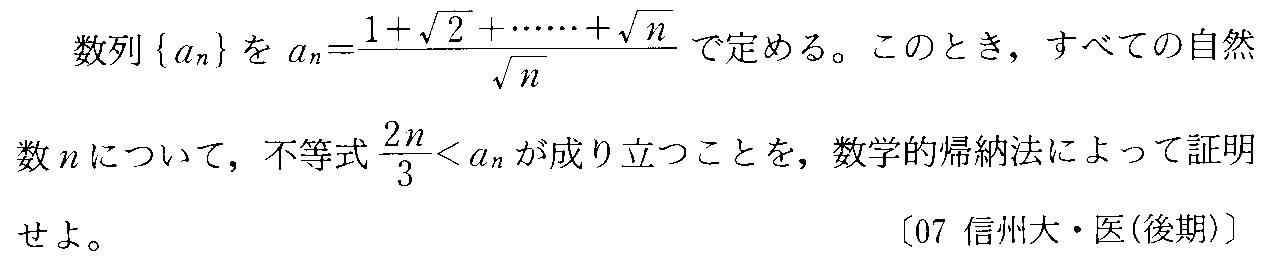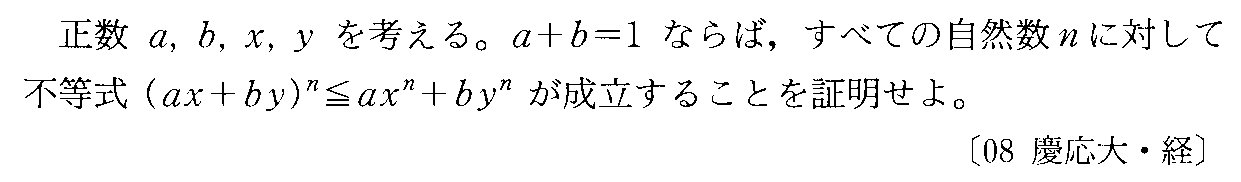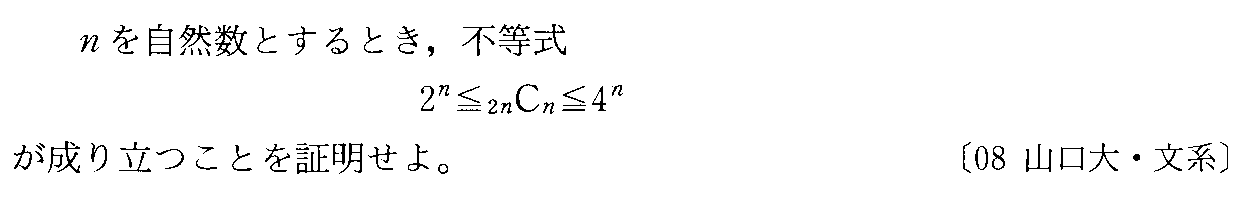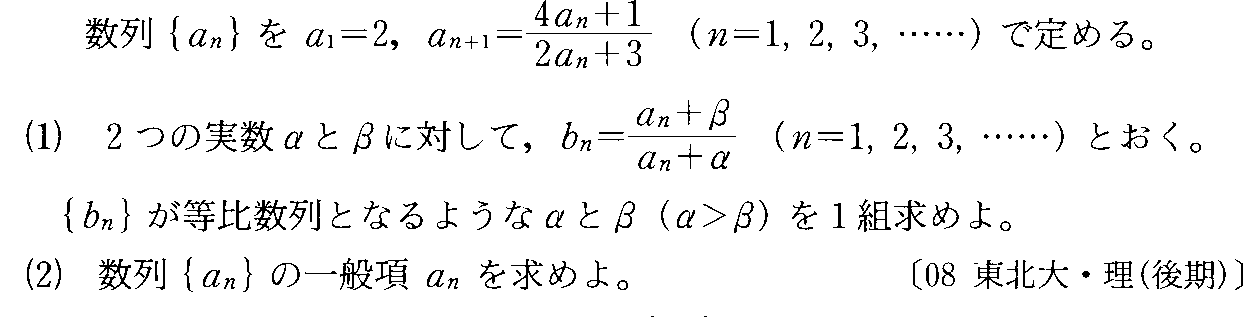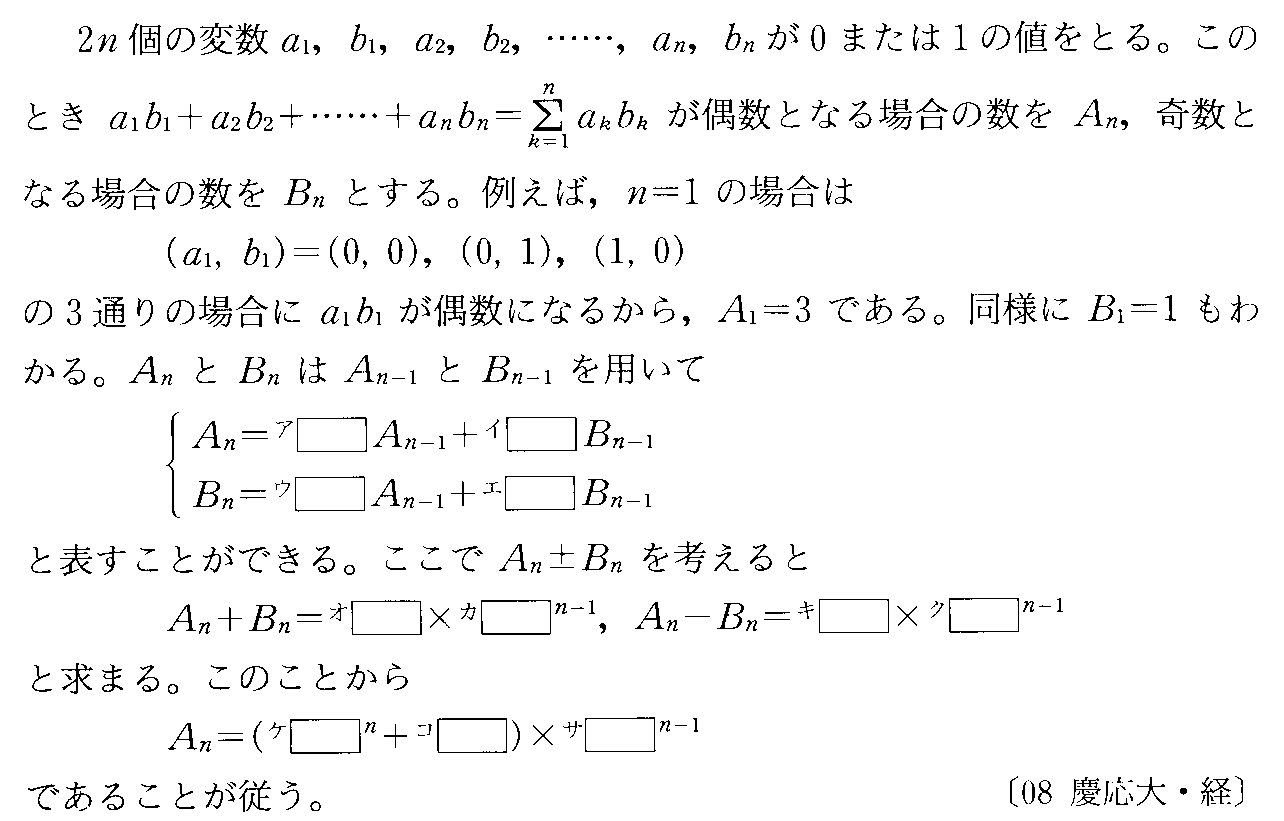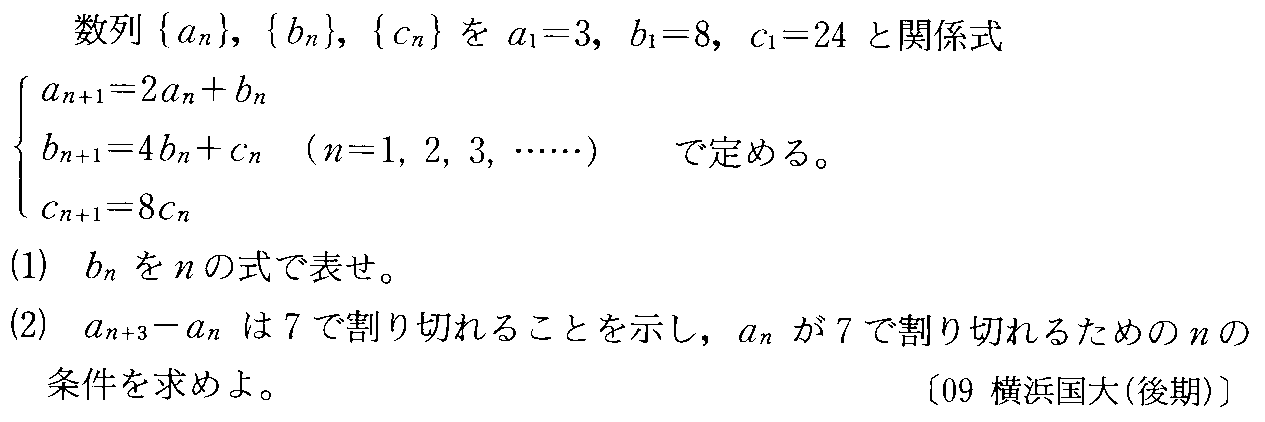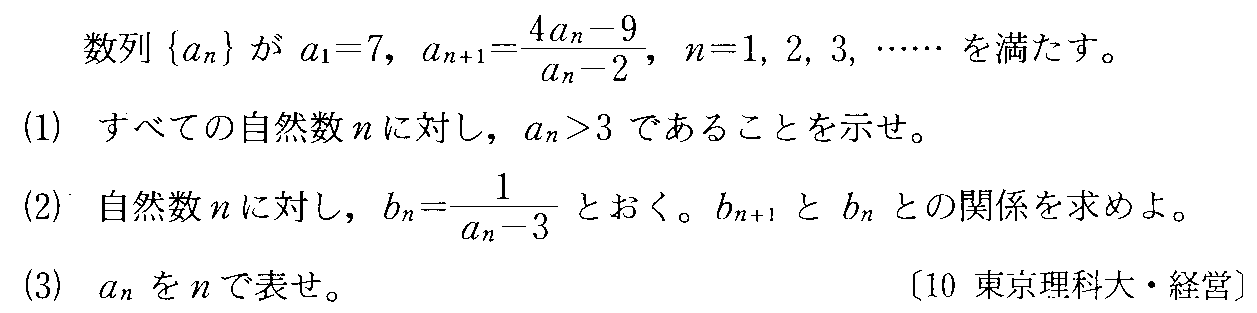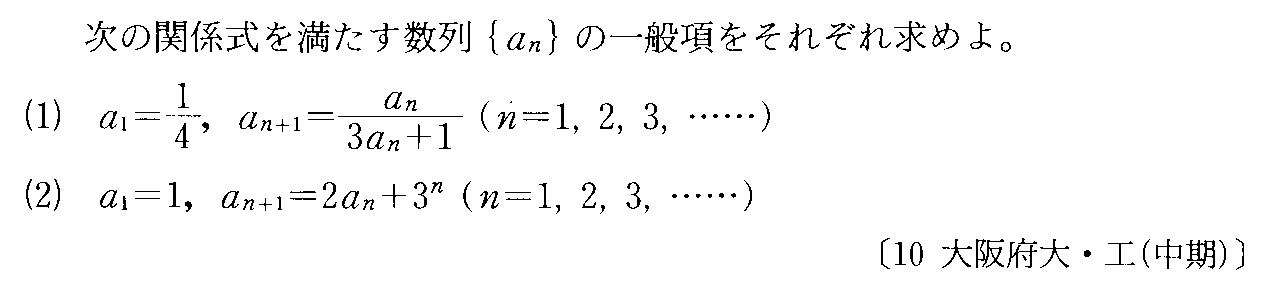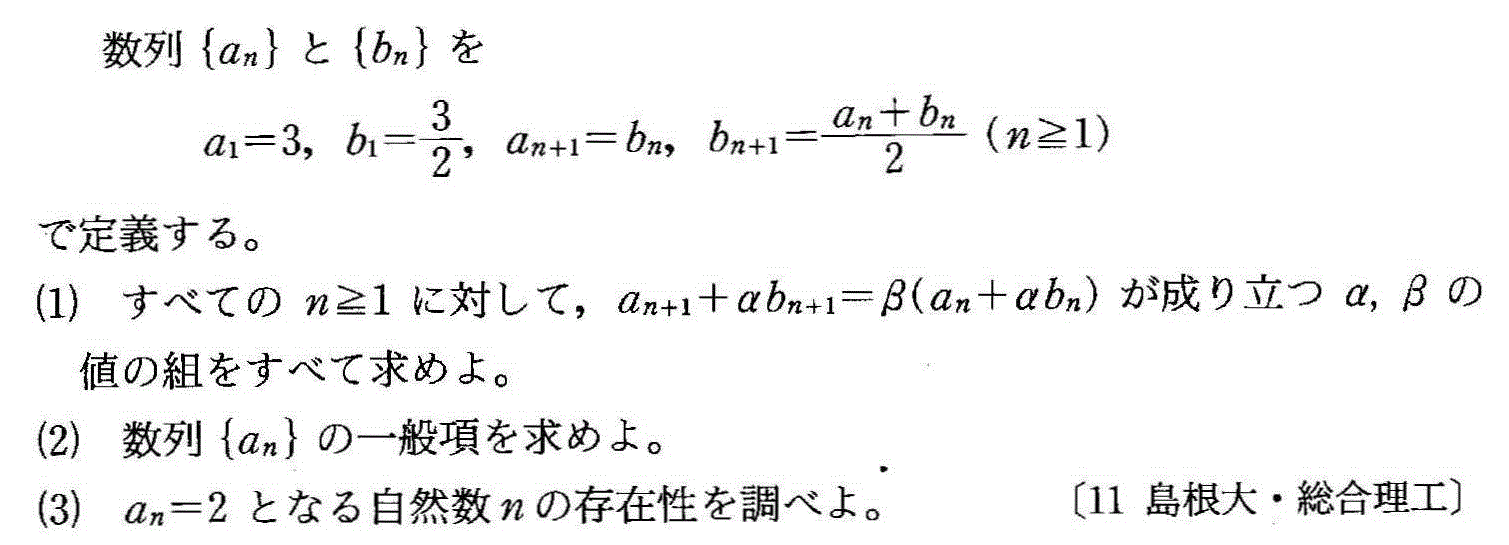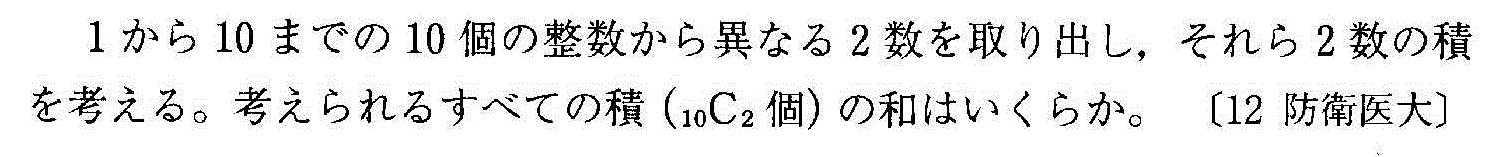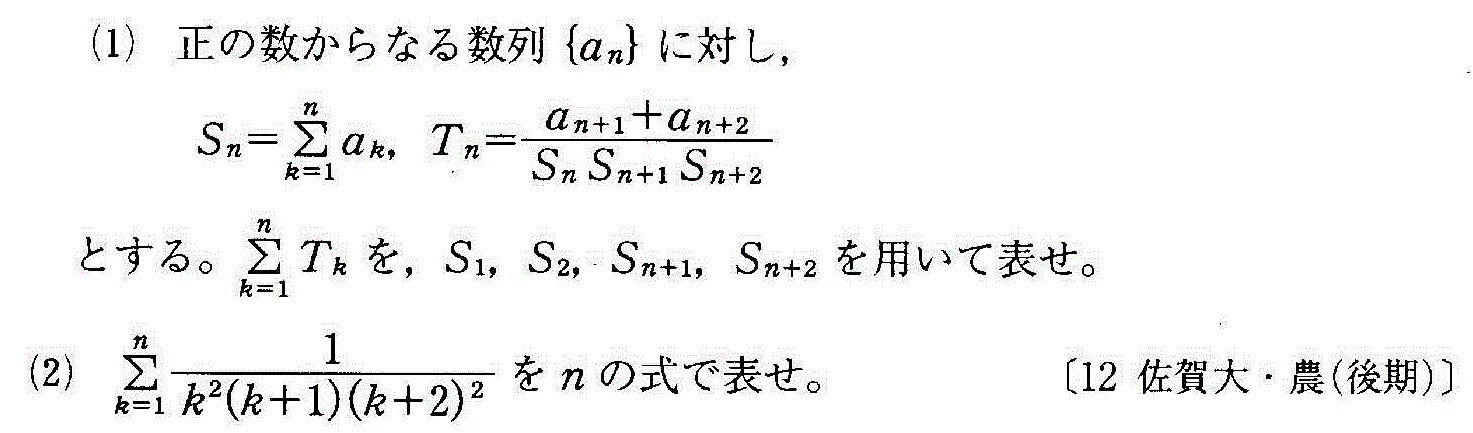1. [2000b138_1]
   
   
   
2. [2000b138_2]
   
   
   
3. [2000b142_2]
   
   
   
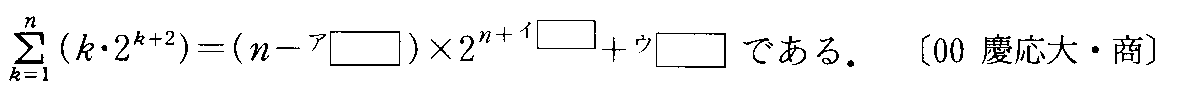
4. [2000b146]
   
   
   
5. [2000b150]
   
   
   
6. [2000b158]
   
   
   
7. [2000b160]
   
   
   
8. [2000r147]
   
   
   
9. [2000r152]
   
   
   
10. [2000r153]
    
    
    
11. [2000r155]
    
    
    
12. [2000r160]*隣接3項間漸化式(特性方程式の解がいずれも1でない場合)・和から一般項を求める
    
    
    
13. [2000r166]
    
    
    
14. [2000r167]*数学的帰納法、等号成立の条件
    
    
    
15. [2000r168]
    
    
    
16. [2001b131]
    
    
    
17. [2001b132]
    
    
    
18. [2001b135_2]
    
    
    
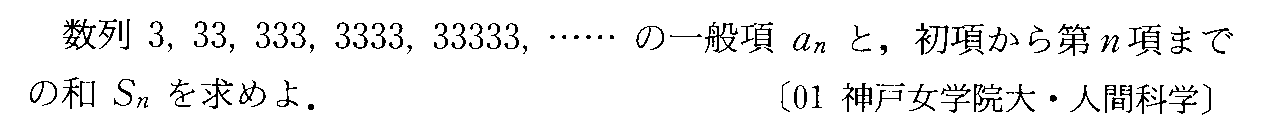
19. [2001b136]
    
    
    
20. [2001b140]*群数列
    
    
    
21. [2001b144]*すべての項が正の数列ならば、対数をとってもよい
    
    
    
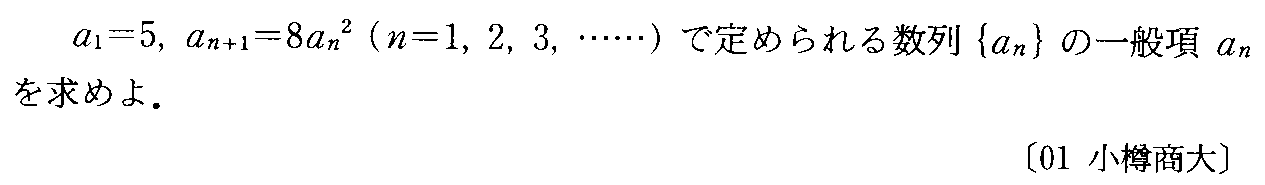
22. [2001b147]
    
    
    
23. [2001b151]
    
    
    
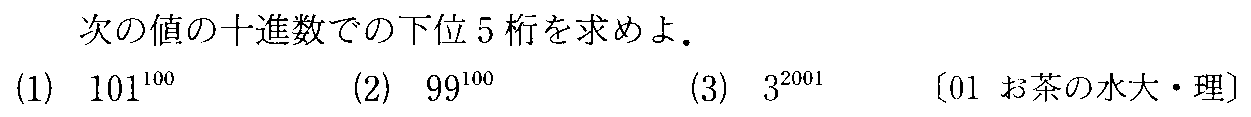
24. [2001b152]
    
    
    
25. [2001b155]
    
    
    
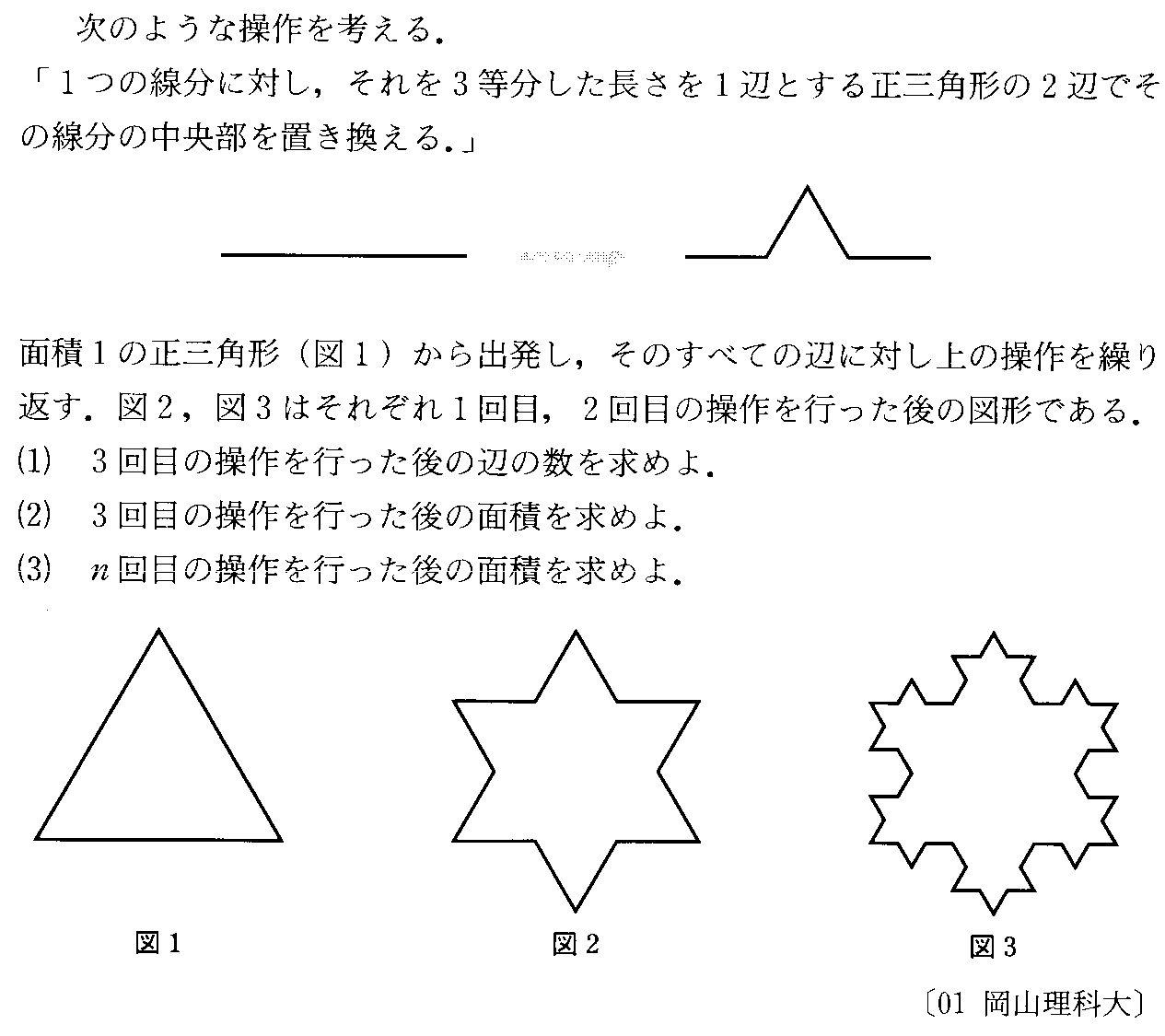
26. [2002b128]*部分分数の差に展開する
    
    
    
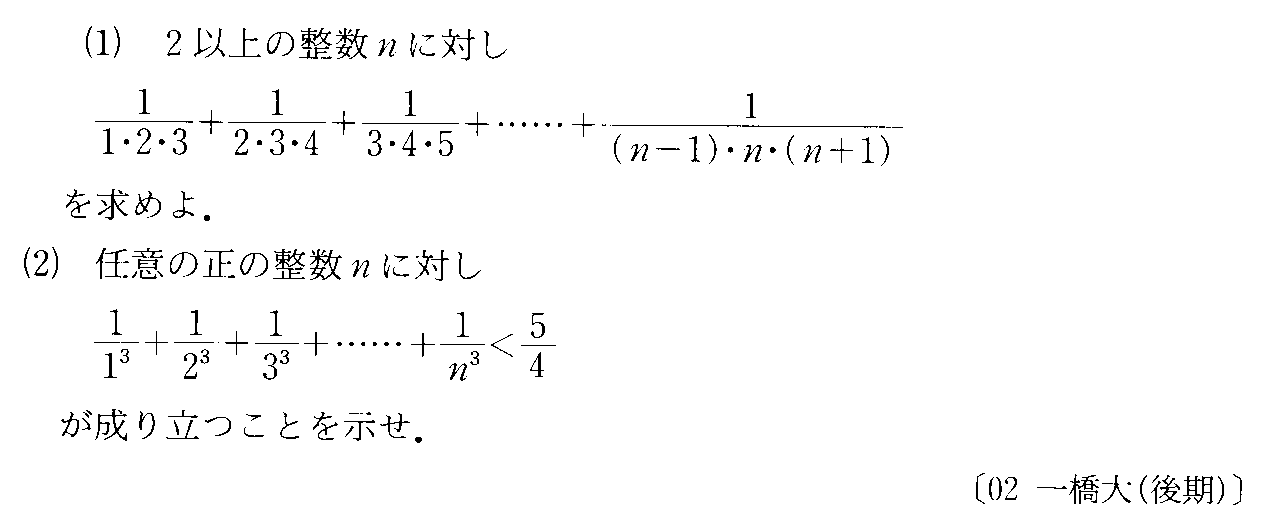
27. [2002b134]
    
    
    
28. [2002b144]
    
    
    
29. [2002b147]*群数列
    
    
    
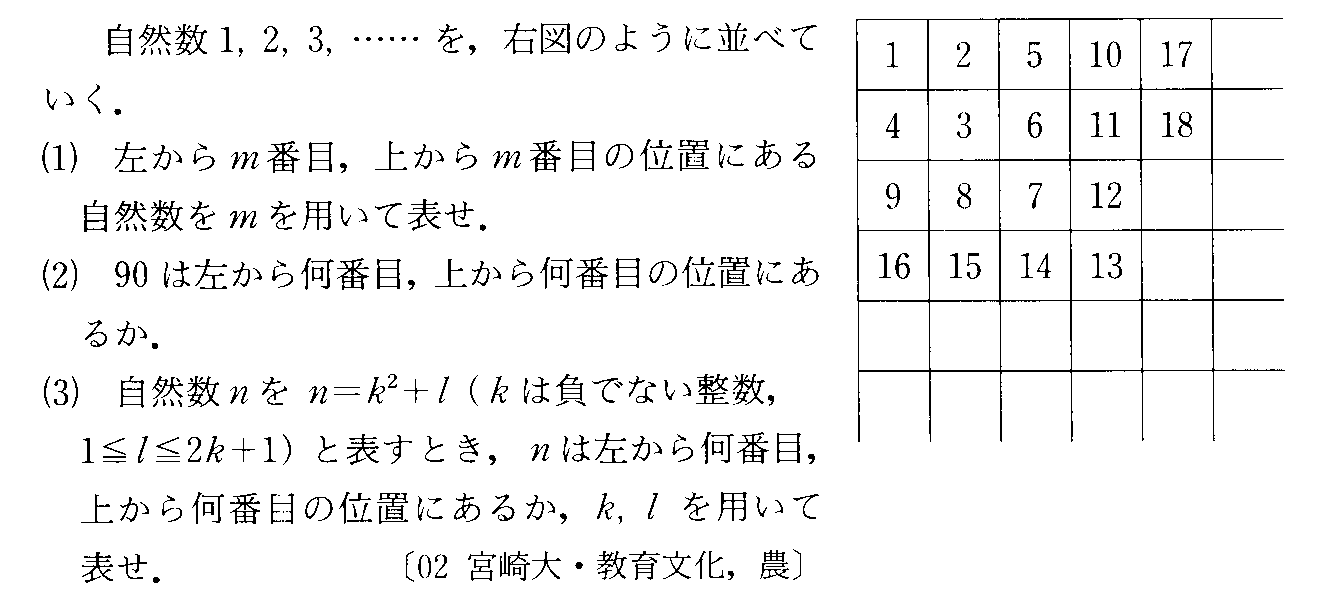
30. [2002r131]
    
    
    
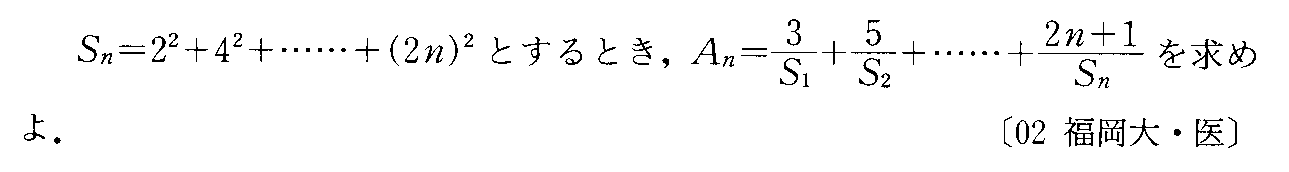
31. [2002r134]
    
    
    
32. [2002r146]
    
    
    
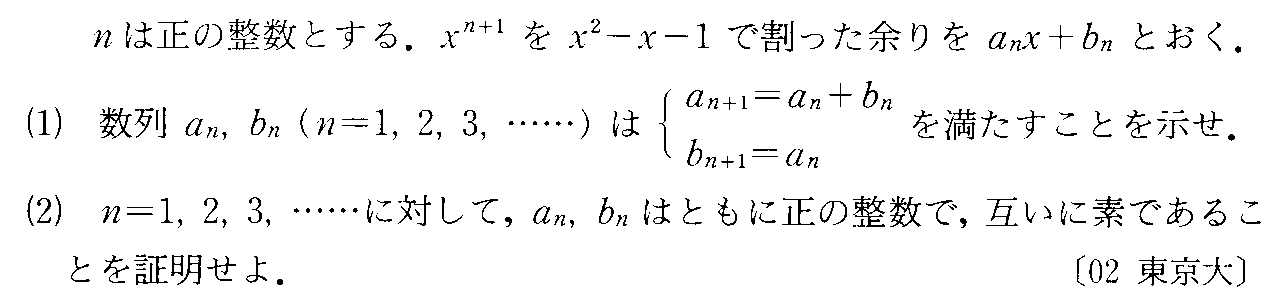
33. [2002r147]
    
    
    
34. [2003b123]
    
    
    
35. [2003b130]
    
    
    
36. [2003b138]
    
    
    
37. [2003b140_1]
    
    
    
38. [2003r124_2]
    
    
    
39. [2003r125]
    
    
    
40. [2003r129]
    
    
    
41. [2003r131]
    
    
    
42. [2003r134]*分数関数型漸化式
    
    
    
43. [2003r142]
    
    
    
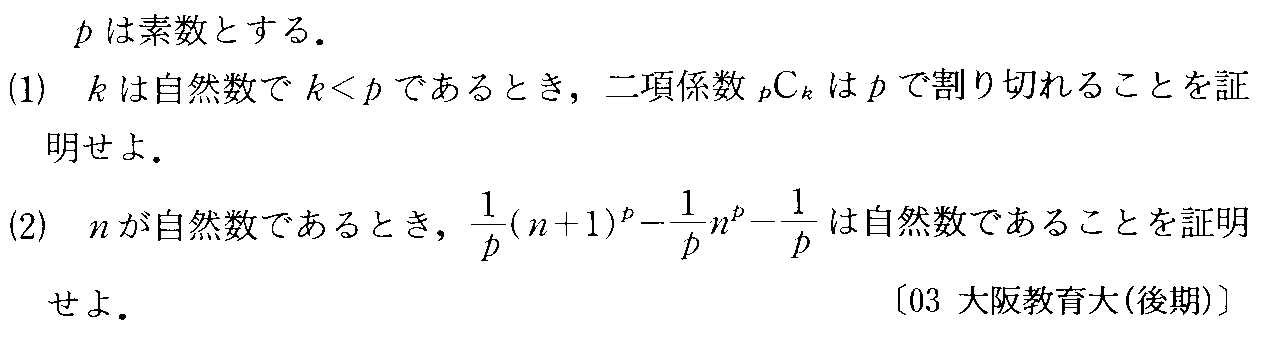
44. [2004b125]
    
    
    
45. [2004b126]
    
    
    
46. [2004b129_2]
    
    
    
47. [2004b131]
    
    
    
48. [2004b134_2]
    
    
    
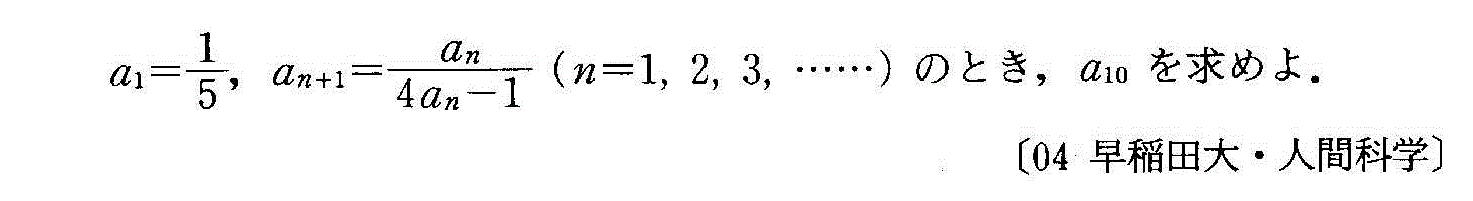
49. [2004r136]*連立漸化式・特性方程式が重解をもつ隣接3項間漸化式
    
    
    
50. [2004r139]
    
    
    
51. [2004r150]*格子点問題
    
    
    
52. [2005r249_1]
    
    
    
53. [2006b276]
    
    
    
54. [2006b277]
    
    
    
55. [2006r270_1]
    
    
    
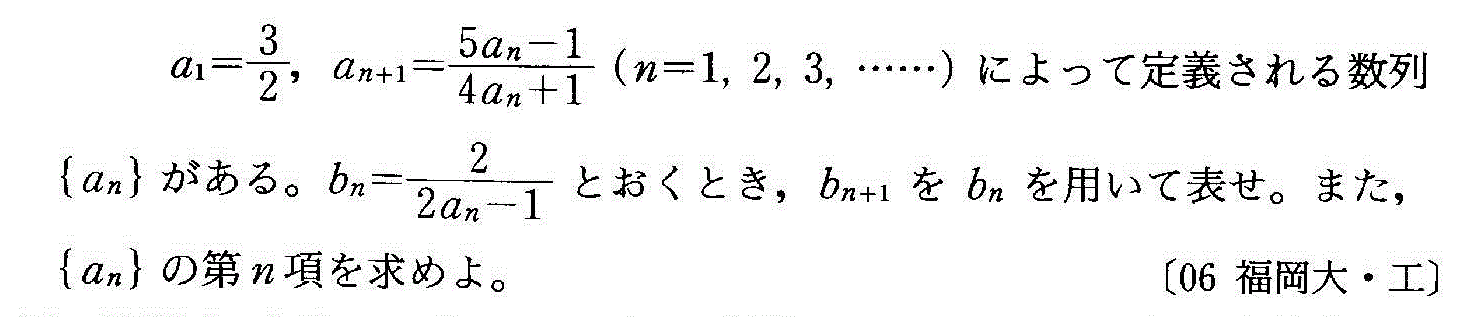
56. [2007b256]
    
    
    
57. [2007r259]*｢余事象｣の考え方
    
    
    
58. [2007r273]
    
    
    
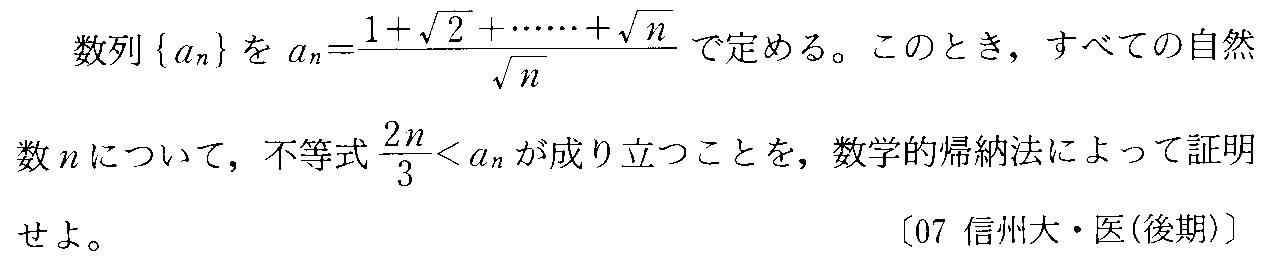
59. [2008b255]
    
    
    
60. [2008b259]
    
    
    
61. [2008b260]*｢等差｣×｢等比｣型数列の和
    
    
    
62. [2008b270_3]*数学的帰納法
    
    
    
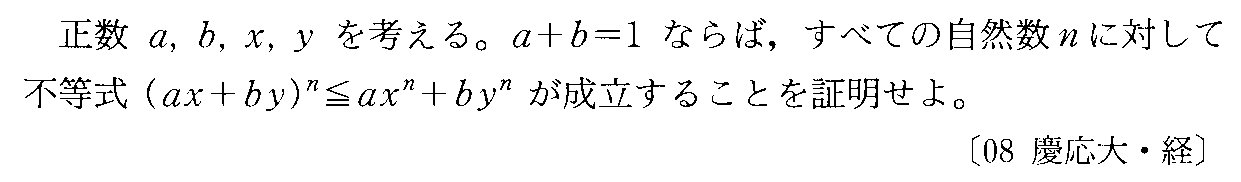
63. [2008b271]
    
    
    
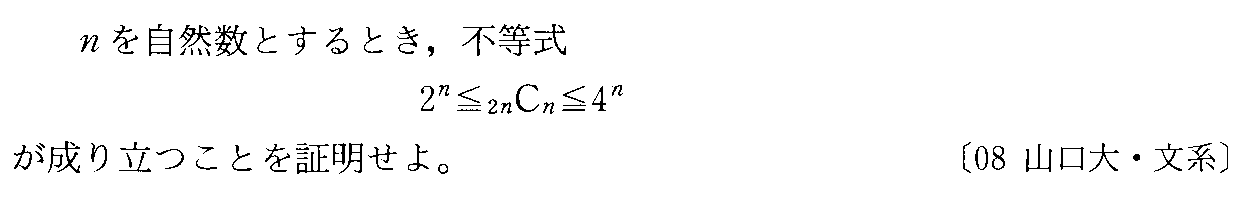
64. [2008r253]
    
    
    
65. [2008r257]
    
    
    
66. [2008r262]
    
    
    
67. [2008r264]
    
    
    
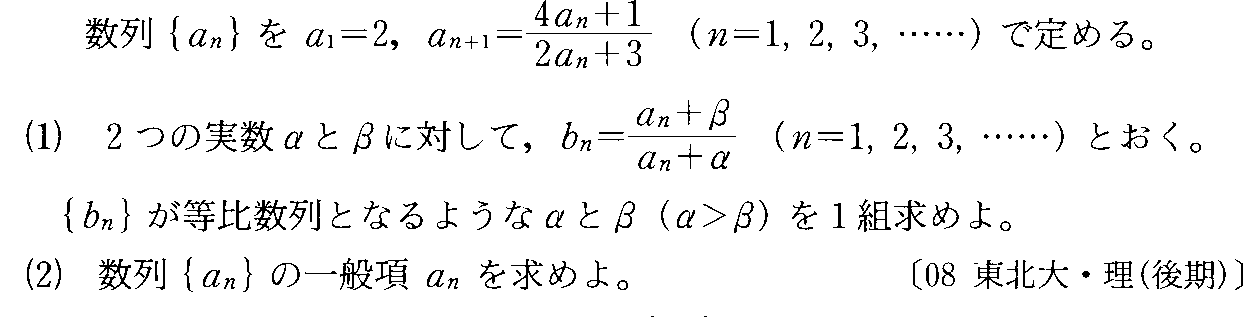
68. [2008r266]
    
    
    
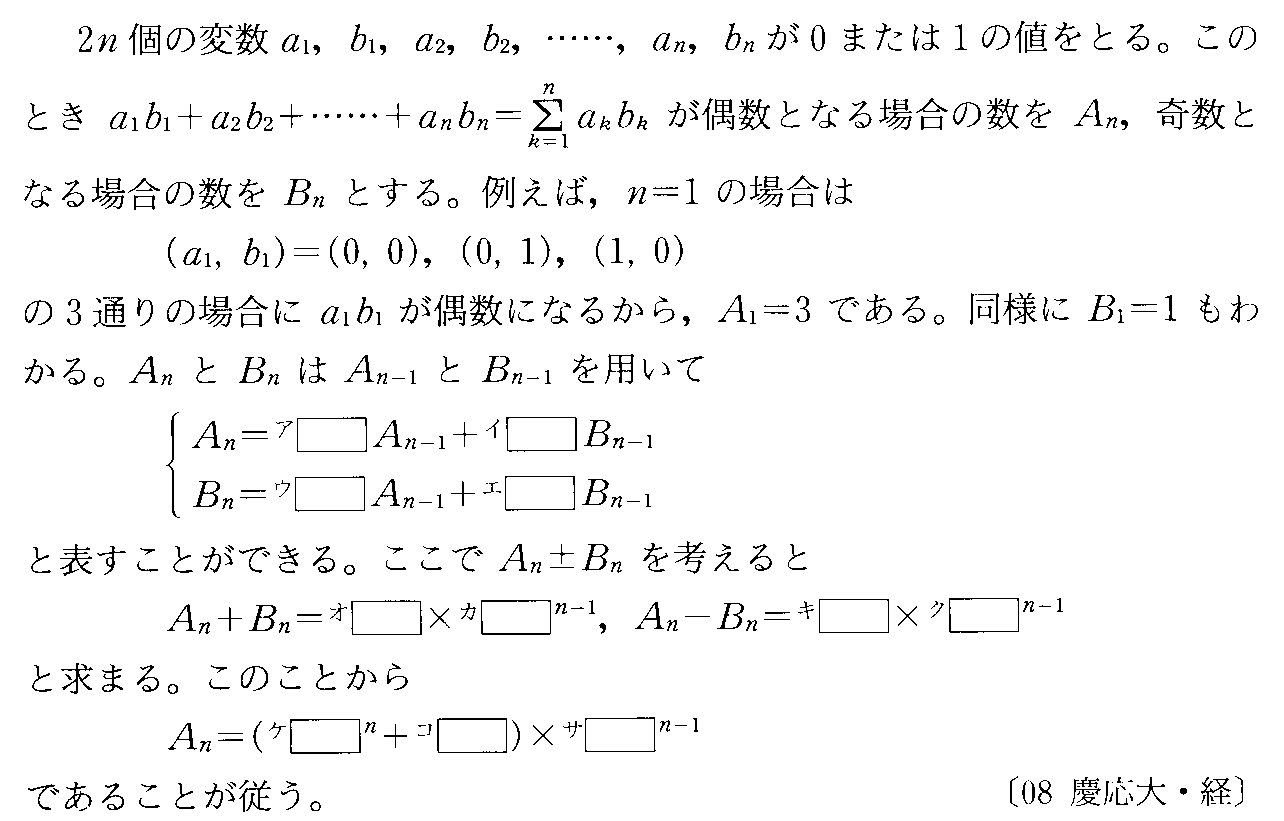
69. [2008r267]
    
    
    
70. [2008r270]
    
    
    
71. [2008r273]
    
    
    
72. [2009b250]
    
    
    
73. [2009b253]*群数列
    
    
    
74. [2009b255]*整数の正の約数の個数、その和
    
    
    
75. [2009b258]
    
    
    
76. [2009b260]
    
    
    
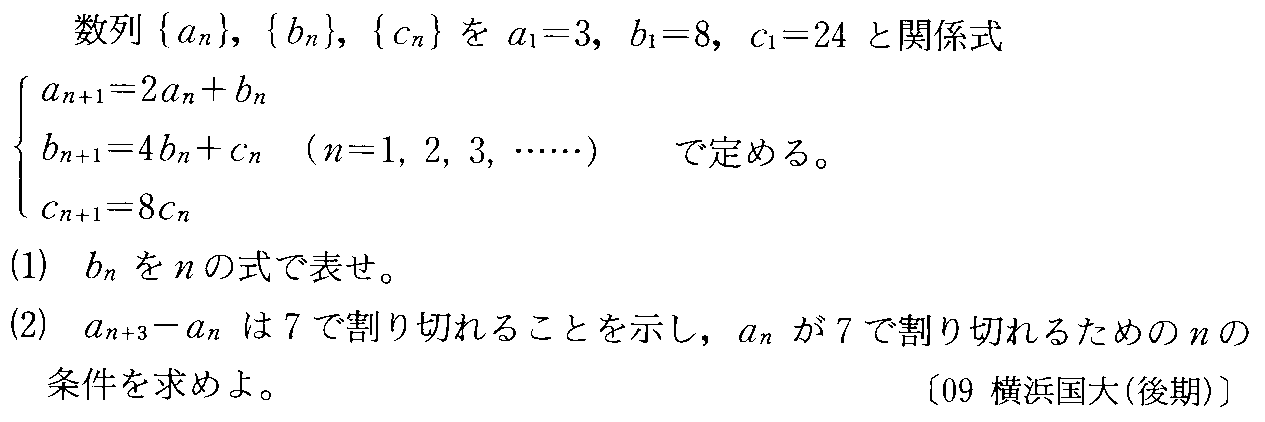
77. [2009b264]
    
    
    
78. [2009b265]*一般項の推定と帰納法による証明
    
    
    
79. [2009b267]
    
    
    
80. [2009b268]
    
    
    
81. [2009r261]*連立漸化式
    
    
    
82. [2009r264]
    
    
    
83. [2009r265]
    
    
    
84. [2010b259]*自然数の累乗の和の公式の導出
    
    
    
85. [2010b260]
    
    
    
86. [2010b263]
    
    
    
87. [2010b266]
    
    
    
88. [2010b268]
    
    
    
89. [2010b270]
    
    
    
90. [2010r262]
    
    
    
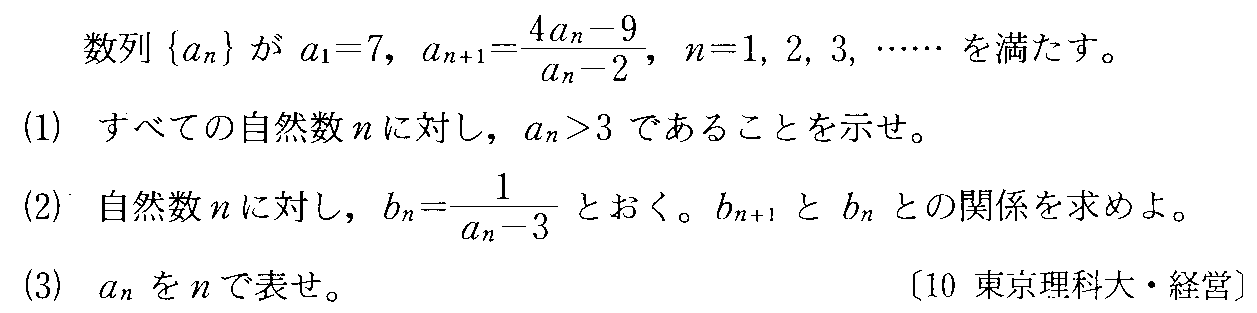
91. [2010r263]
    
    
    
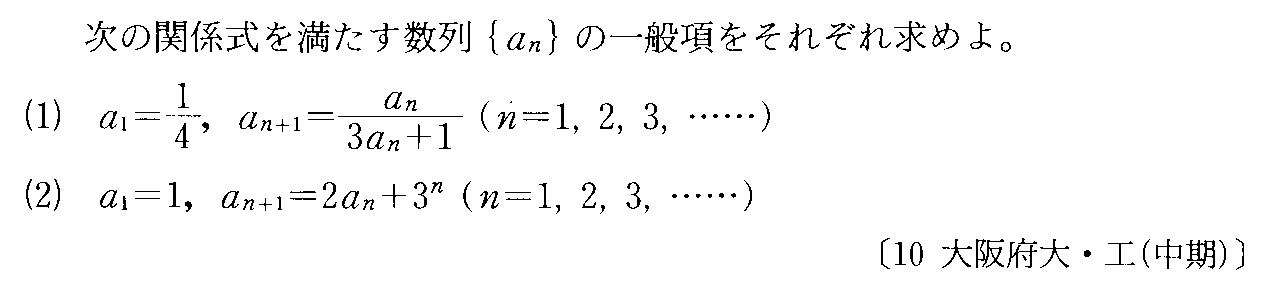
92. [2010r265]
    
    
    
93. [2010r266]
    
    
    
94. [2010r277]
    
    
    
95. [2011r263]
    
    
    
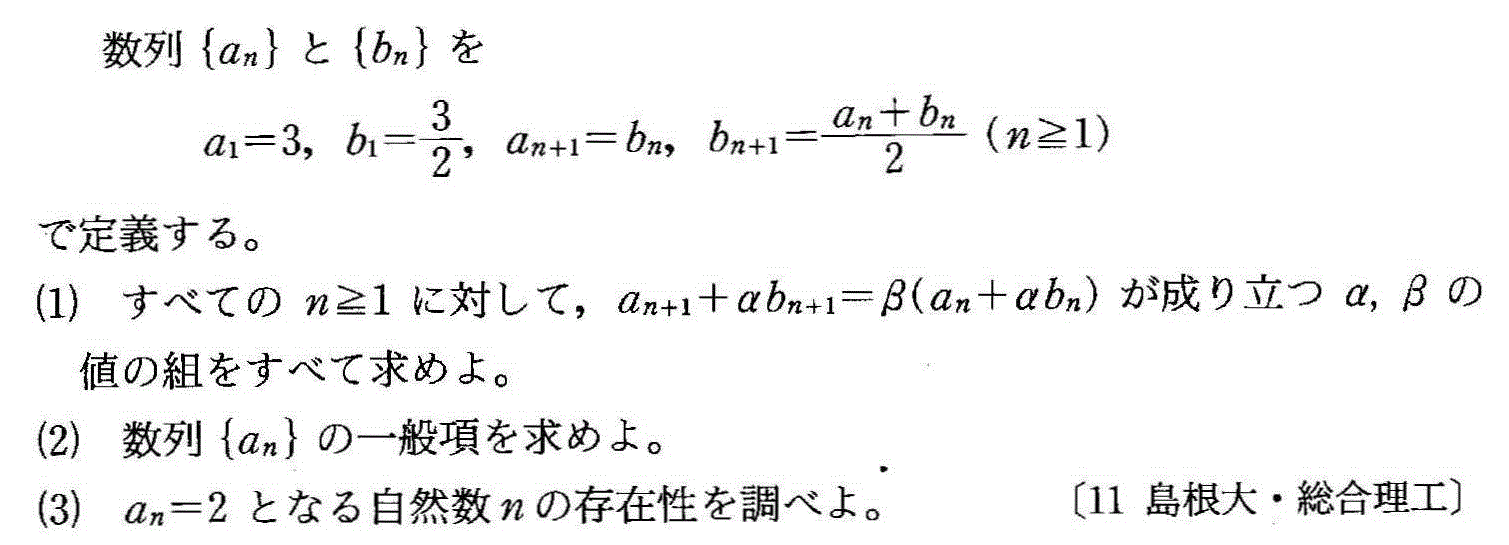
96. [2012r251]
    
    
    
97. [2012r252]
    
    
    
98. [2012r253]
    
    
    
99. [2012r255]
    
    
    
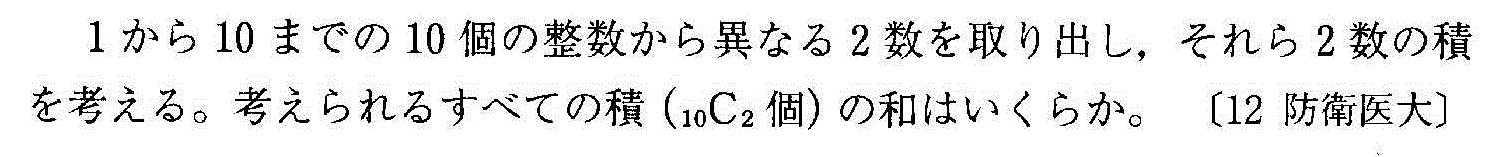
100. [2012r257]
     
     
     
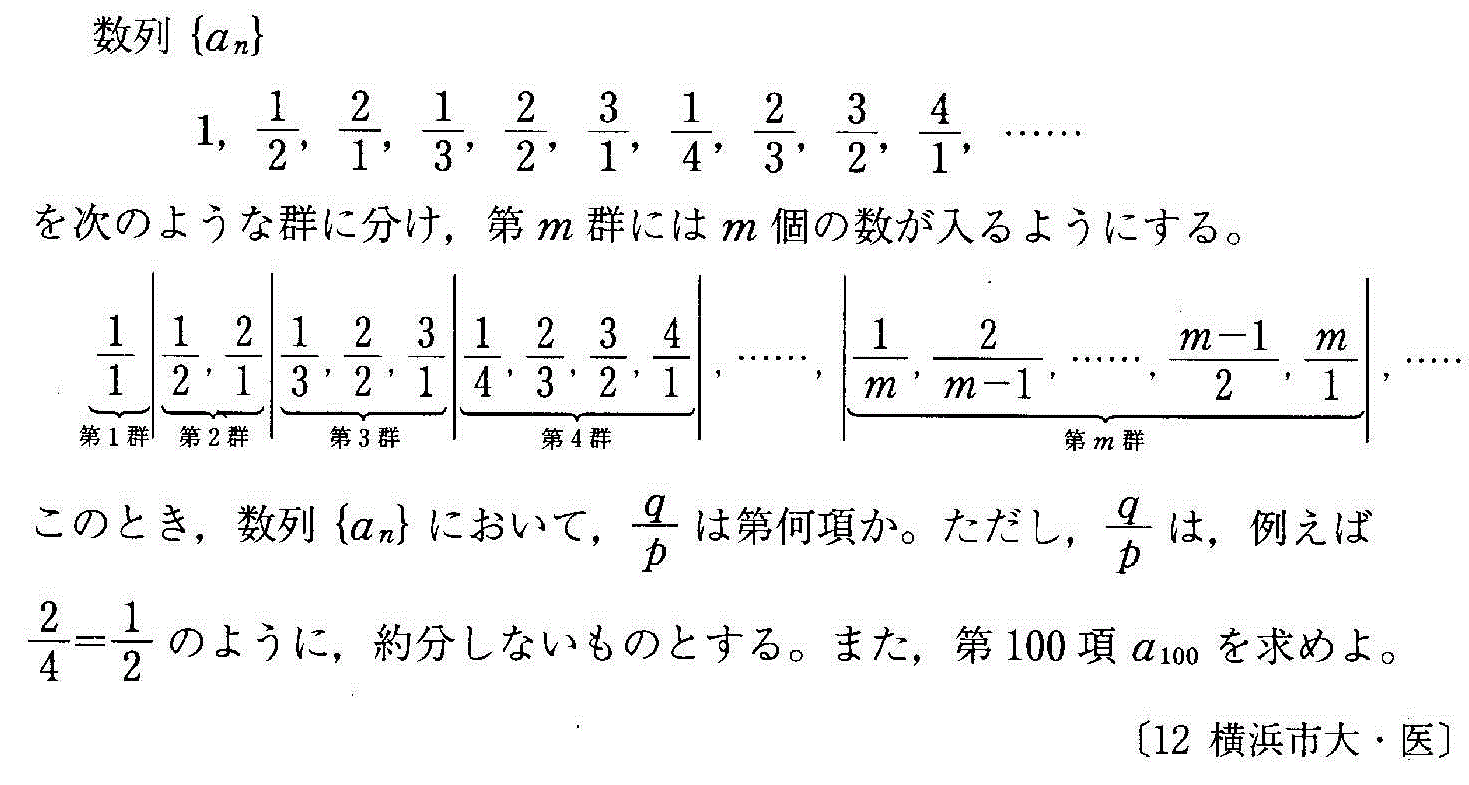
101. [2012r258]
     
     
     
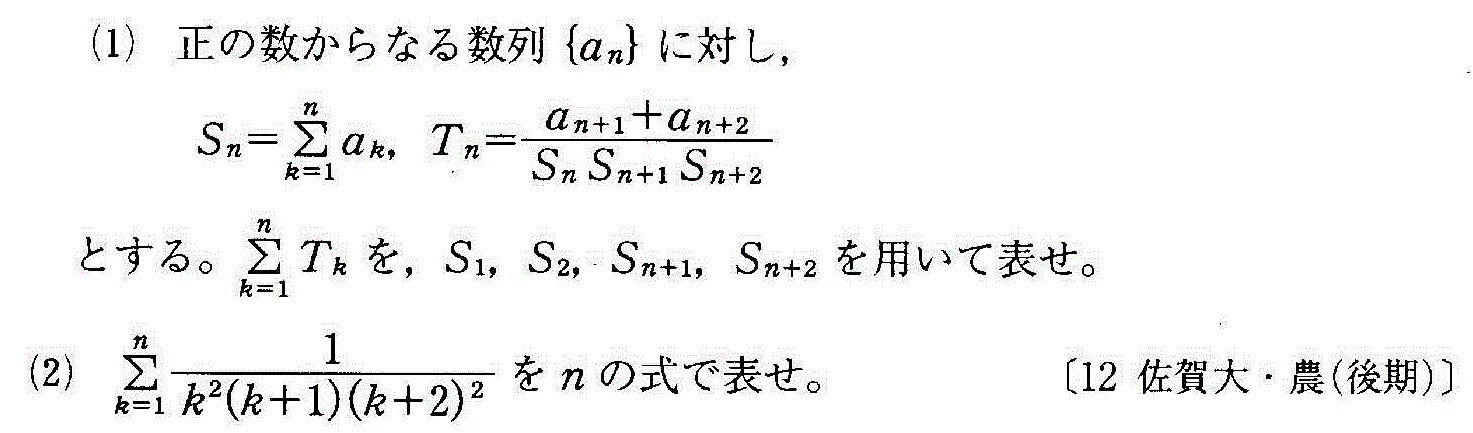
102. [2012r263]
     
     
     
103. [2012r264]*隣接3項間漸化式、定数項を含む場合
     
     
     
104. [2012r266]
     
     
     
105. [2012r268]
     
     
     
106. [2012r269]
     
     
     
107. [2012r273]*3次元格子点問題
     
     
     
108. [2012r274]