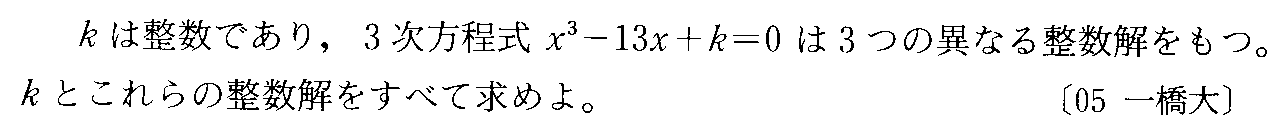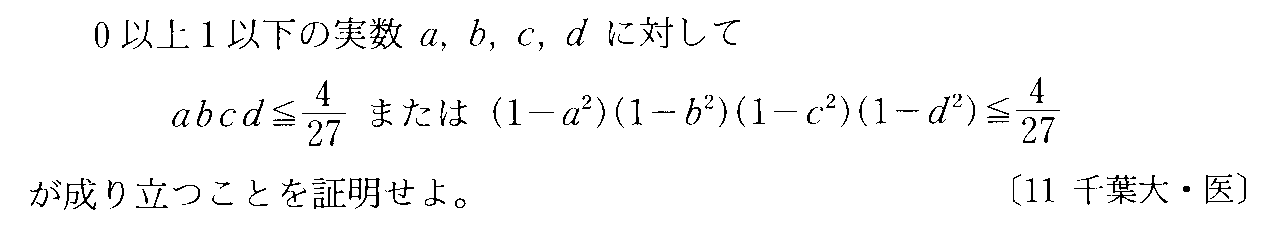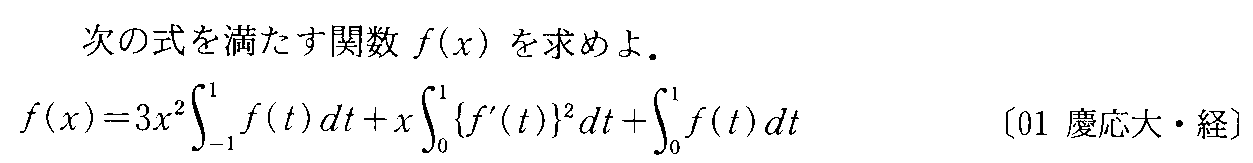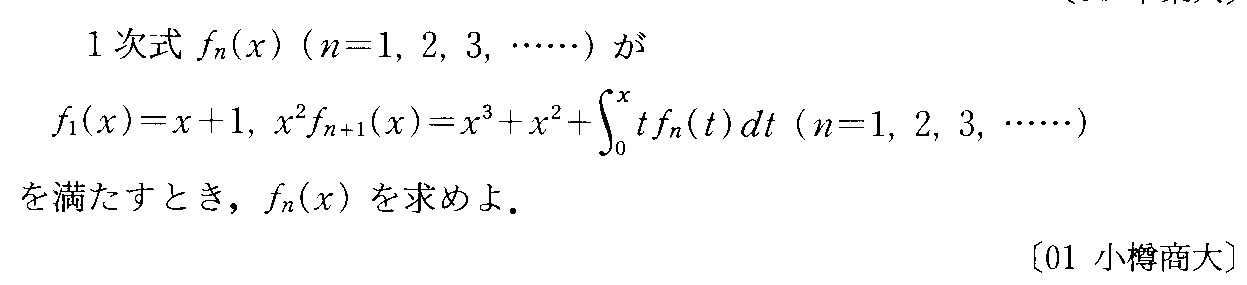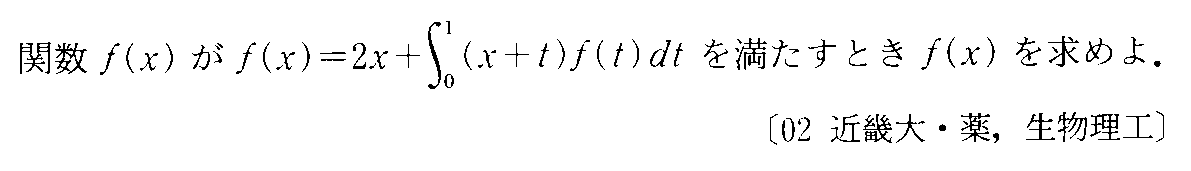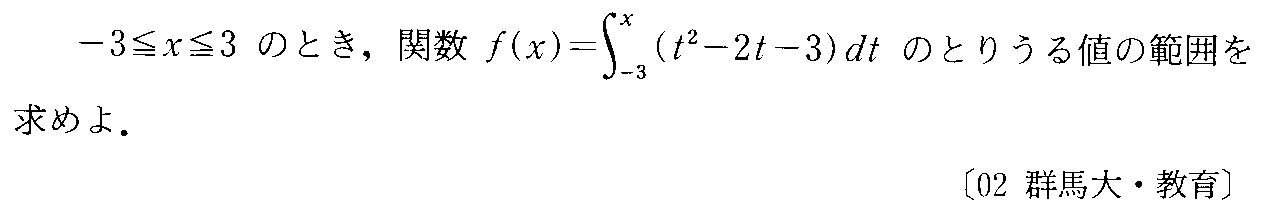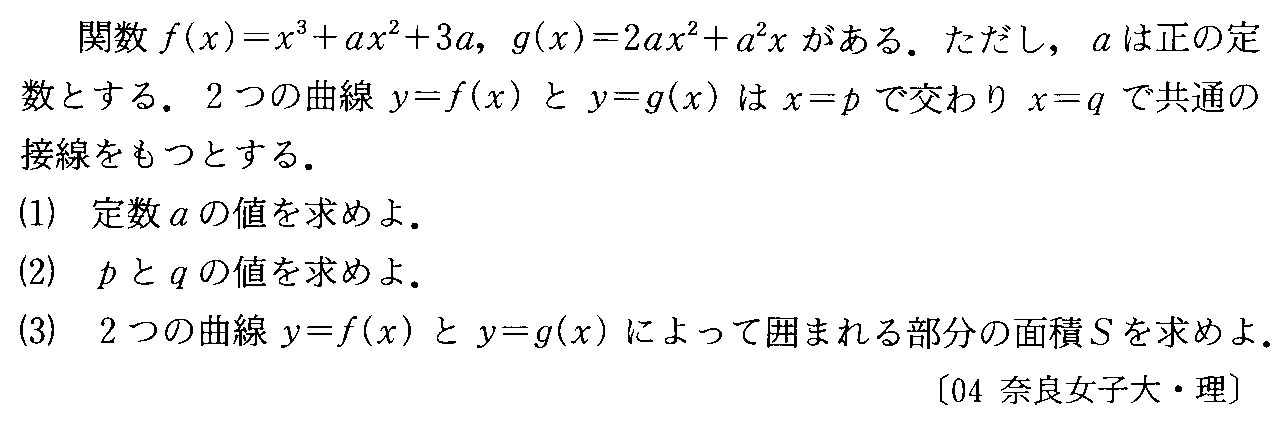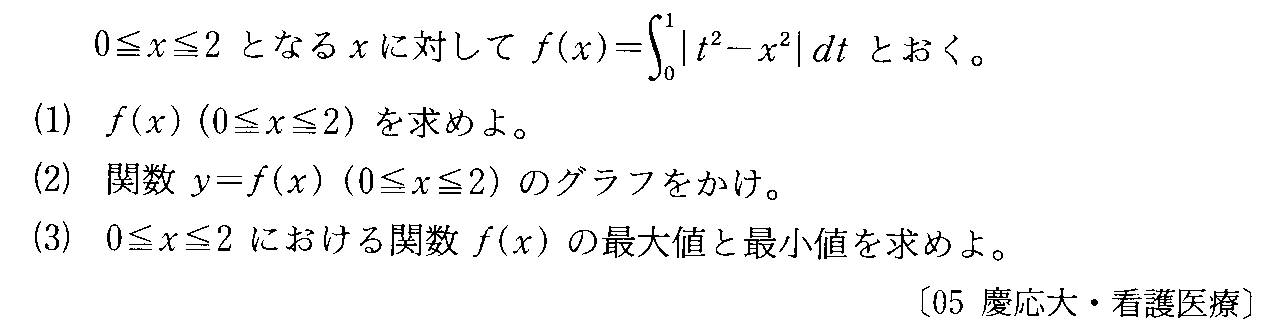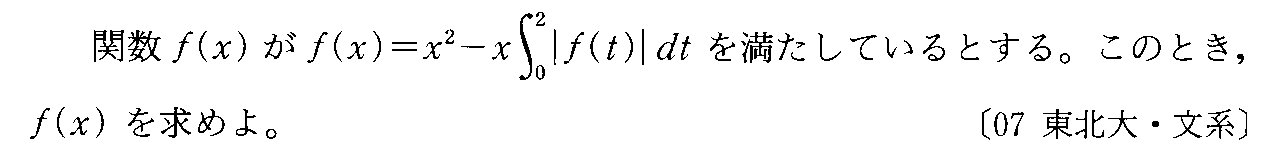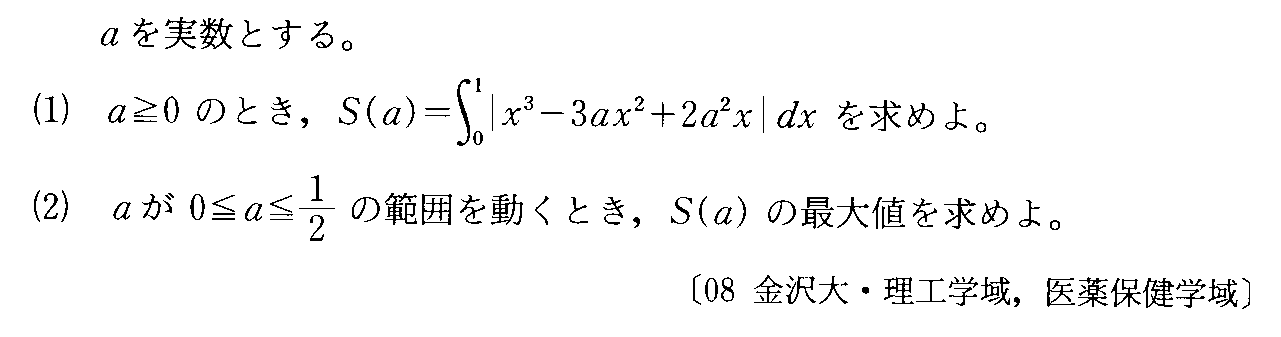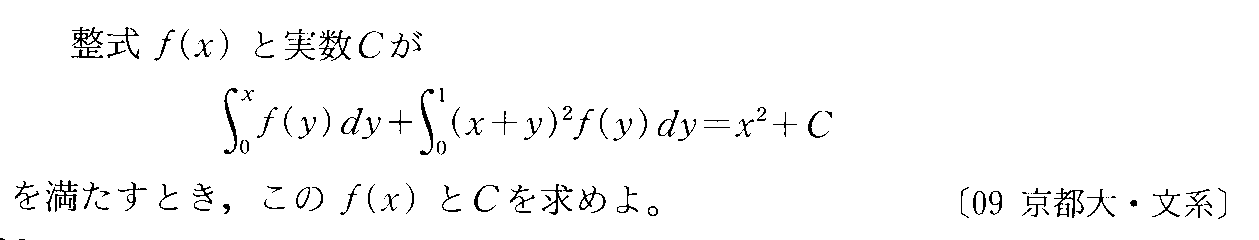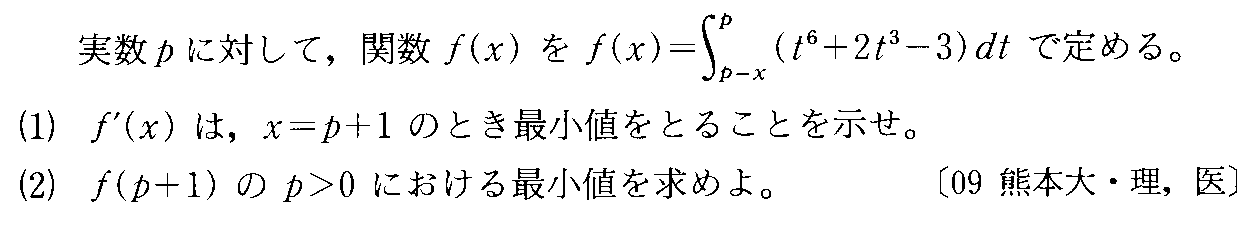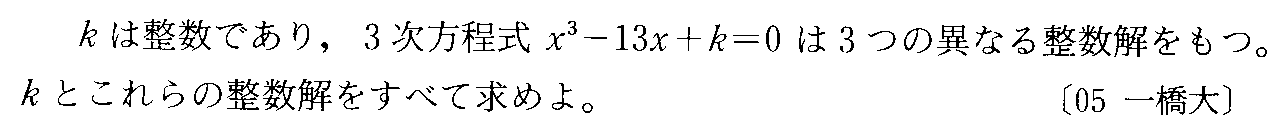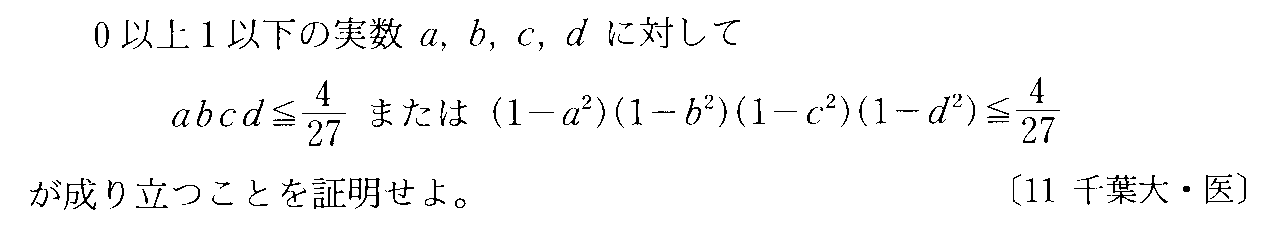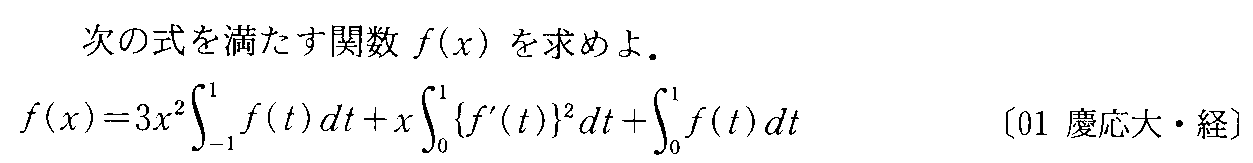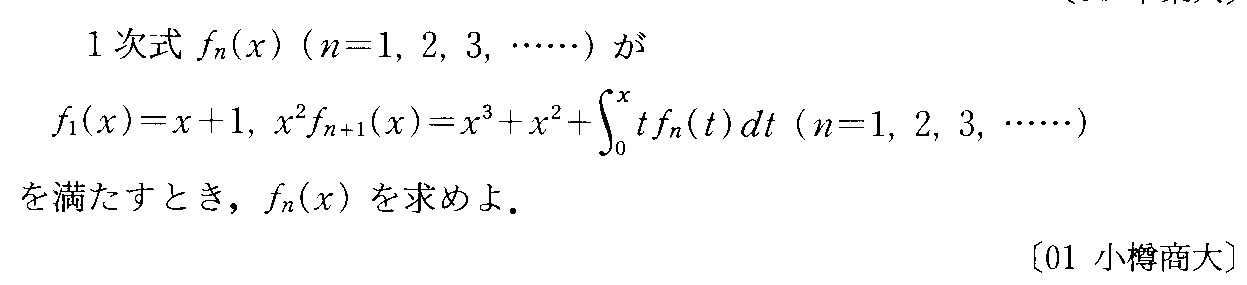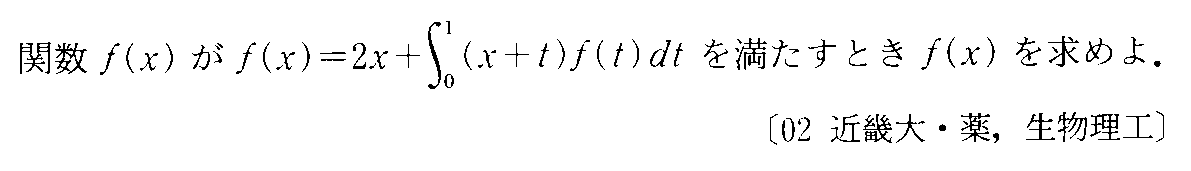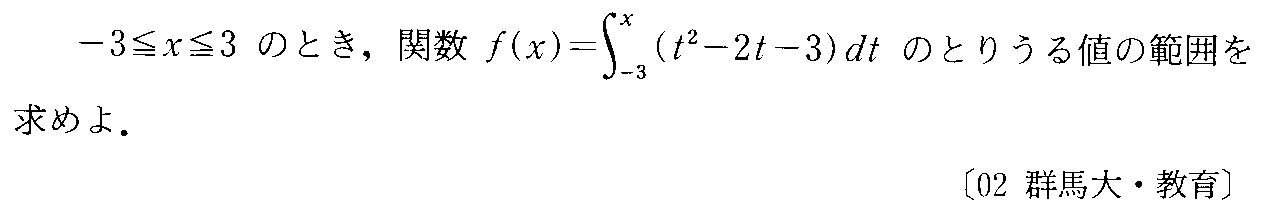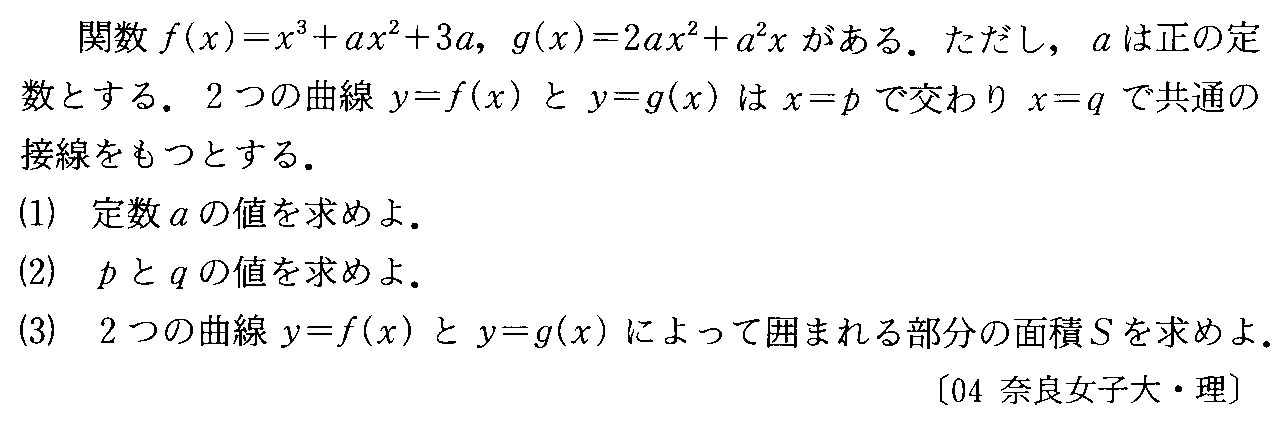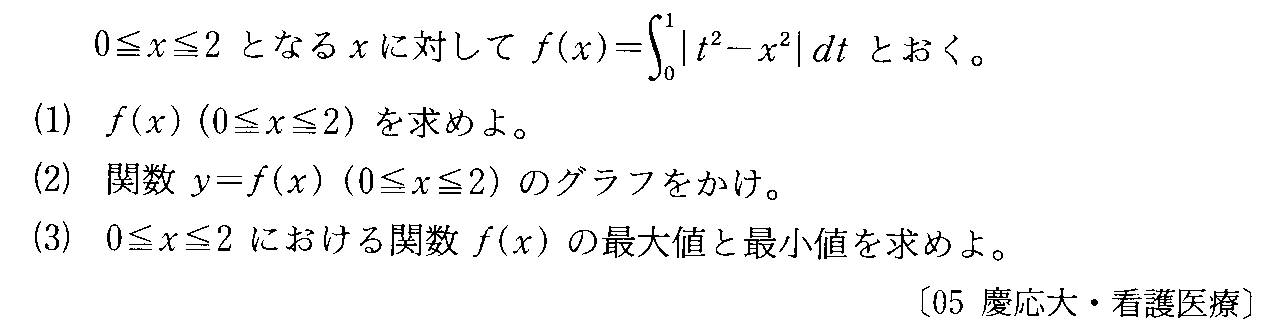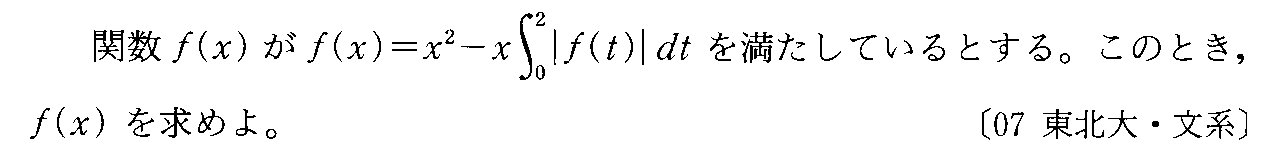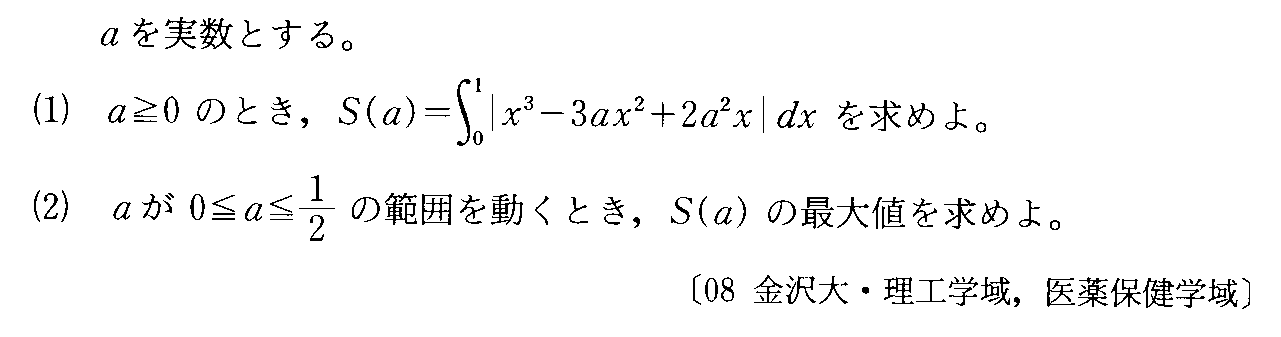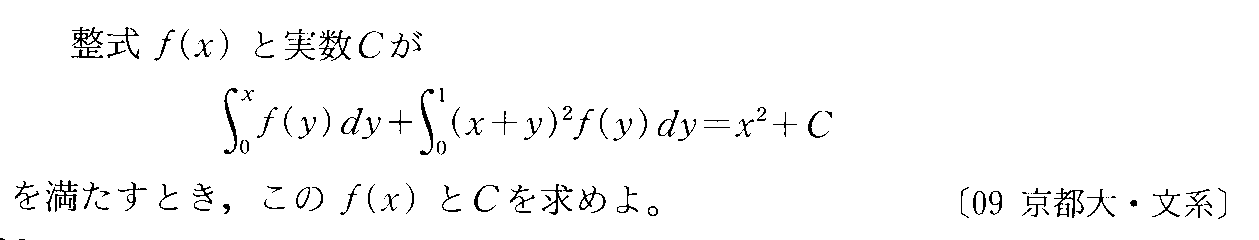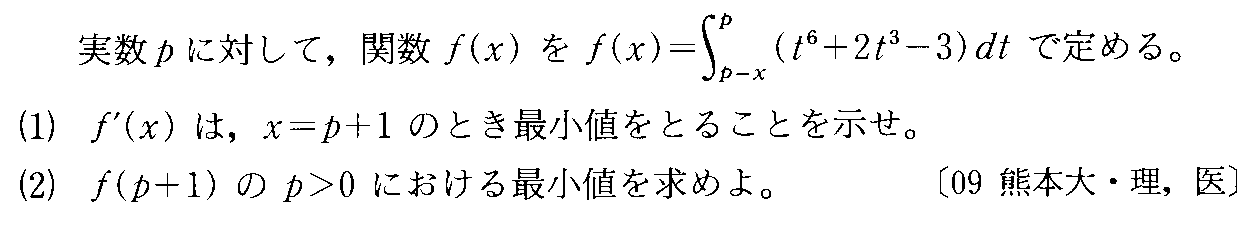微分

[2000b169]

[2000b174]

[2000b181]*3次関数、極大値と同じ値をとる点を求めるには？

[2000b184]

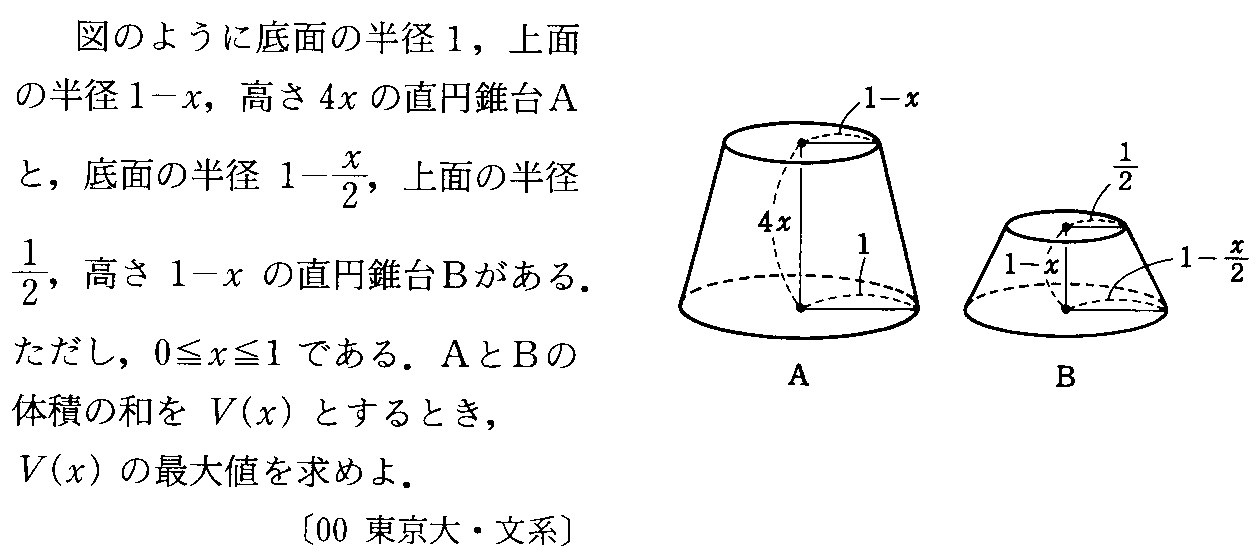
[2000b185_2]

[2000r180]

[2000r185]

[2000r191]*最大最小

[2001b166]

[2002r167]置き換え、最大最小(→｢三角関数｣)

[2002r172]*3次関数に曲線外の1点から引く接線の本数

[2003b167]

[2004b162]*3次関数の点対称性

[2004b169]

[2005b195]置き換え、解の個数(→｢三角関数｣)

[2005r184]

[2005r199]

[2006b202]

[2008b195]

[2008r192]

[2009b193]*3次関数に曲線外の1点から引く接線

[2009b194]

[2009r183]

[2009r187]

[2009r192]

[2010b189]*3次関数の点対称性

[2010b195]

[2010b205]

[2010b206]

[2010r203]*3次関数の点対称性

[2011r200]

[2011r202]

積分

[2000r203]

[2000r217]

[2001b184]

[2001b186]

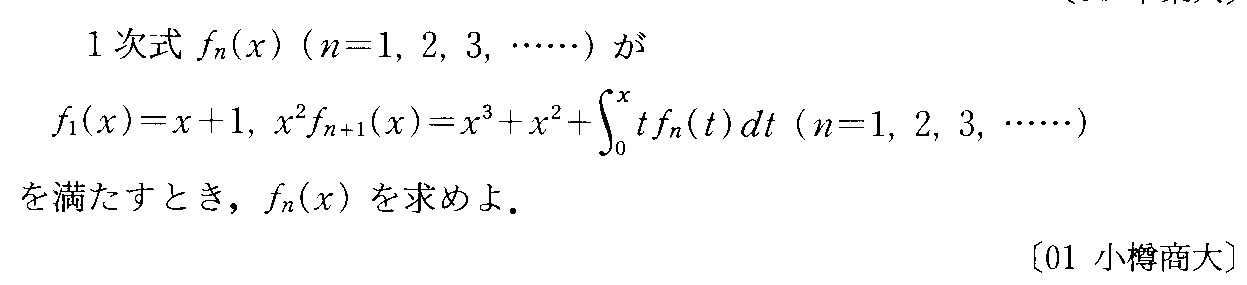
[2001b197]

[2002b176_2]

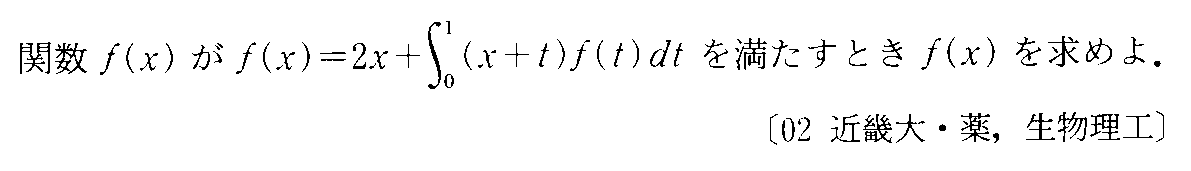
[2002b177]

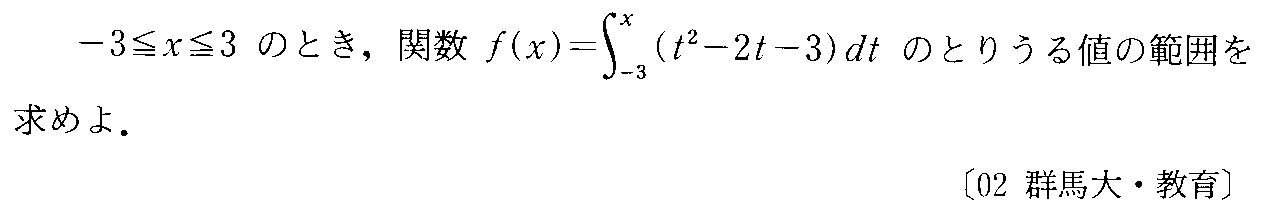
[2002r186]

[2004b188]*｢6分の1｣の面積公式の利用

[2004b191]

[2004r184]*接線を共有する3次関数と2次関数で囲まれた面積

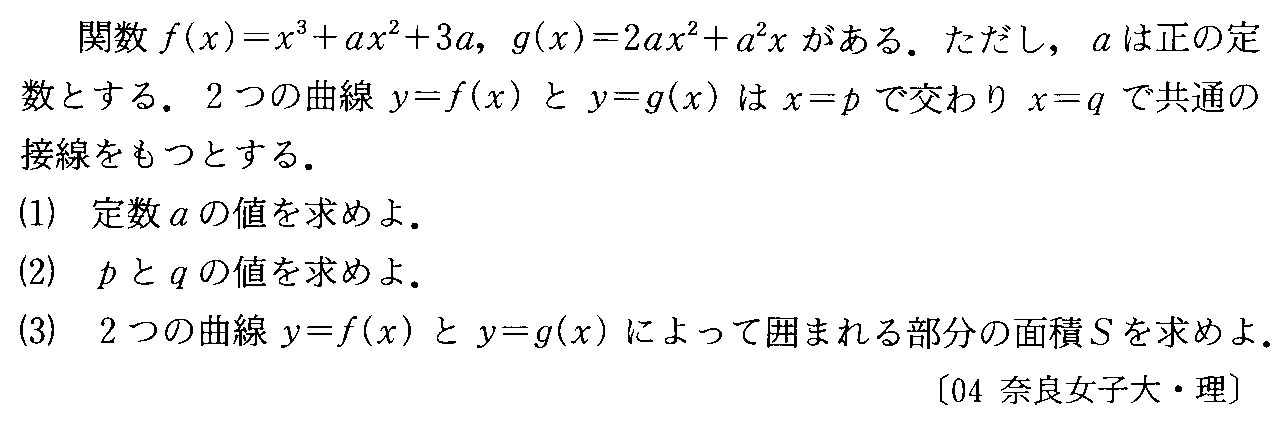
[2004r193]

[2005r205]

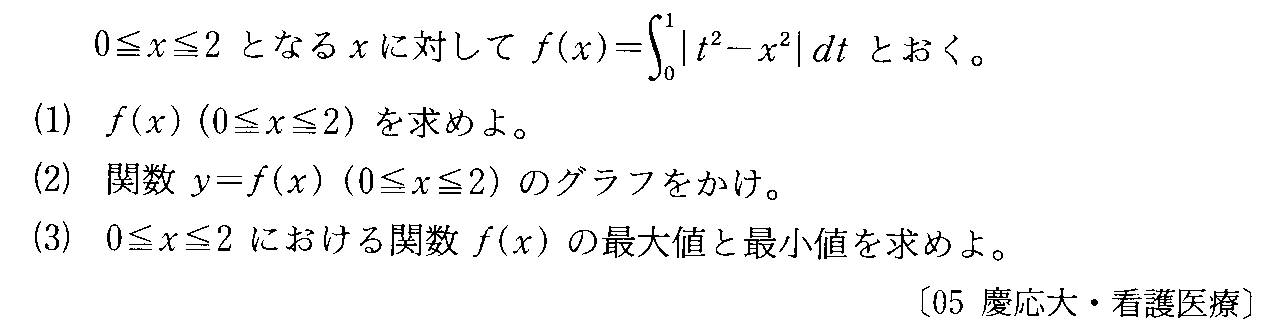
[2007b201]*絶対値記号を含む定積分・定積分を含む式で定義された関数

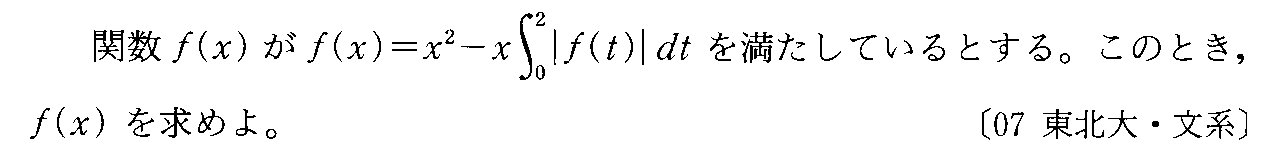
[2007b216]

[2008r210]

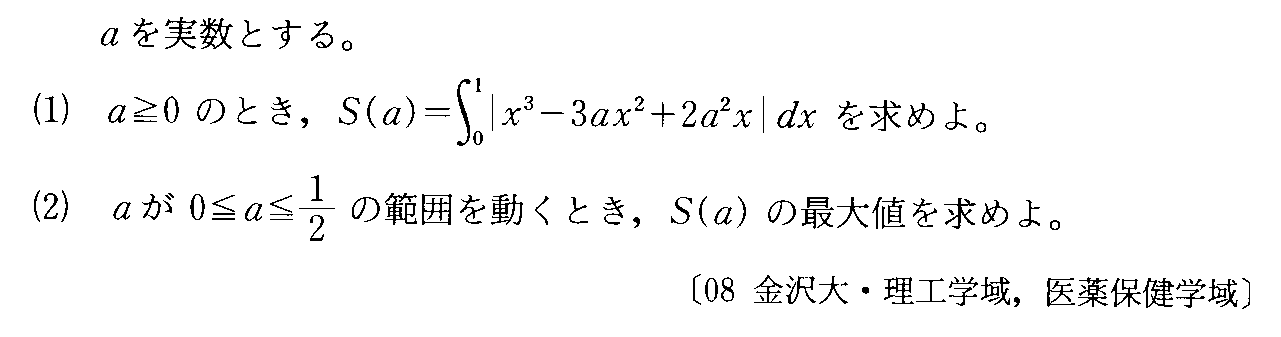
[2009b205]*ニュートンの公式・定積分を含む式で定義された関数

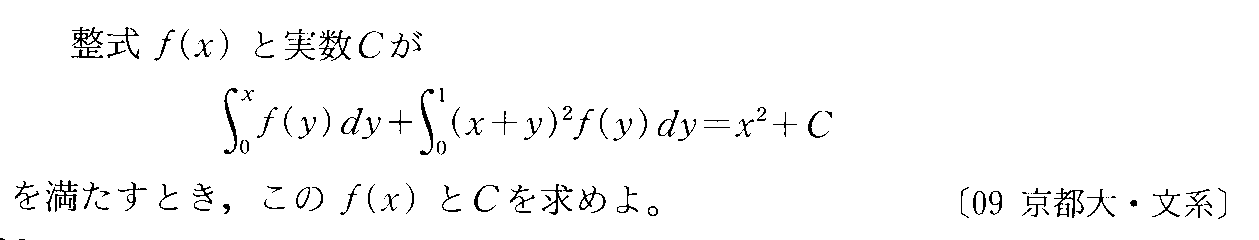
[2009b206]

[2009b210]

[2009b213]

[2009b220]

[2009r203]*原始関数に名前をつける(ニュートンの公式)

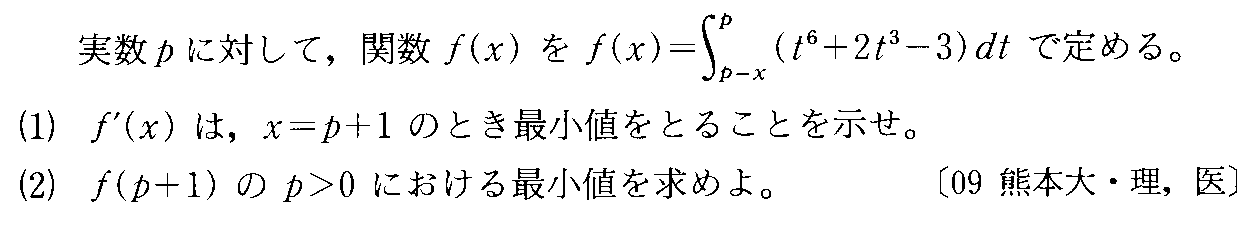
[2009r213]*定数項に未知数を含む3次方程式の解の個数・曲線とその接線で囲まれた図形の面積

[2009r218]

[2010b214]

[2010b221]

[2010b229]

[2010r215]*放物線とその接線で囲まれた図形の面積

[2010r218]

[2011r209]

[2011r210]