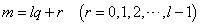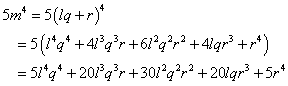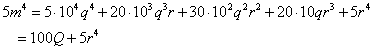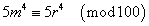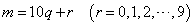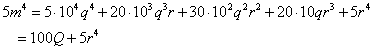m を l で割った商を q 、あまりを r とする。
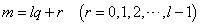
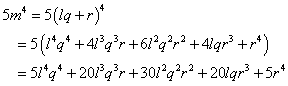
ここで、はじめの4項が、任意の q , r に対して、すべて100の倍数となり、下二桁に影響を及ぼさないためには、
l は、少なくとも5と2を因数にもたなければならない。
そこで、l = 10 とする。
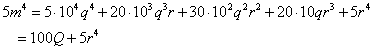
となるから、任意の自然数 m に対する 5m4 の下二桁は、
m の1の位の数 r = 0,1,2,3,4,5,6,7,8,9 に対する 5r4 の下二桁に等しいことがわかった。
「合同式」を用いれば、
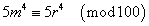
ということができる。
よって、
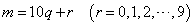
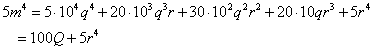
r の各値について、 5r4 の下二桁を調べると、
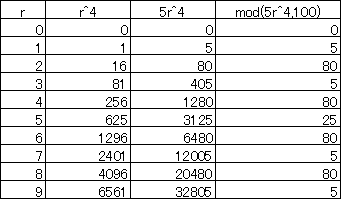
00,05,25,80の4通りに限られることがわかった。
これが求める答えである。
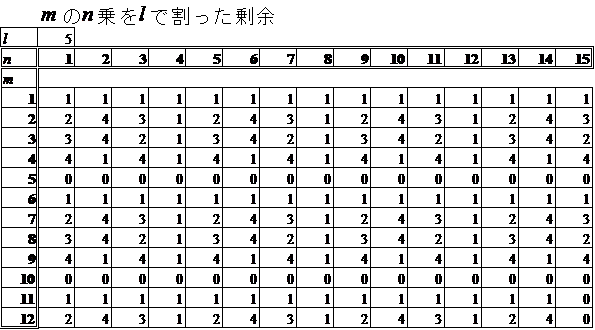
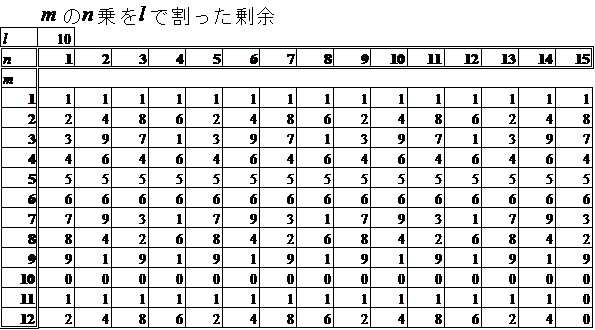
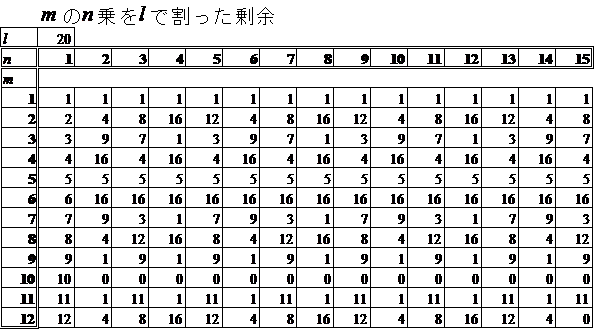
5mn の下二桁に規則性があるか?、ということは、 mn を20で割った余りに規則性があるか?、ってことだろ?
で、つくってみた。