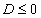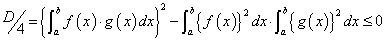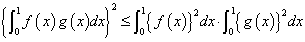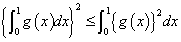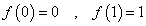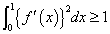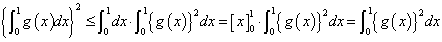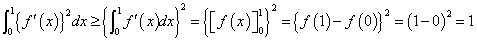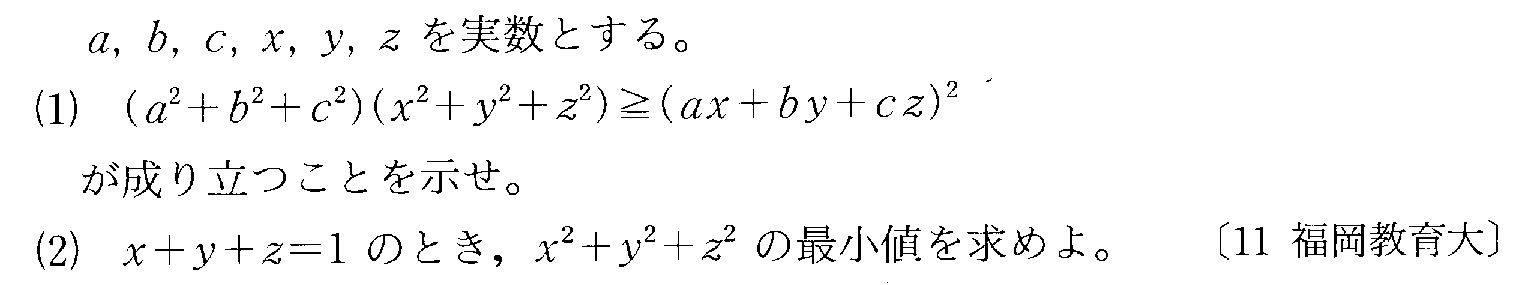実数a,b,c,dに対して、
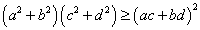
[証明]
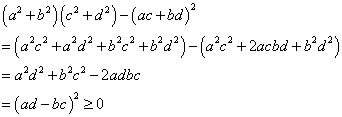
∵ a,b,c,dは、実数だから。
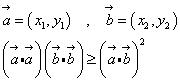
すなわち、
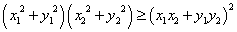
[証明]
 ,
, のなす角をθとすると、
のなす角をθとすると、
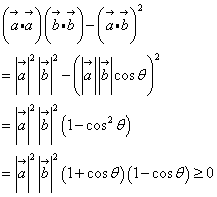
等号成立は、
|
 |=0、すなわち、
|=0、すなわち、 =
=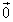 、または、
、または、
|
 |=0、すなわち、
|=0、すなわち、 =
=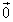 、または、
、または、
cosθ=
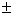 1、すなわち、θ=nπ (nは整数)、
1、すなわち、θ=nπ (nは整数)、
すなわち、
 ,
, が「1次従属」であるとき。
が「1次従属」であるとき。
|
ベクトルの外積
ベクトルa,bのなす角をθとすると、 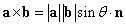
ただし、nは、aがbに重なるように最小の角度で回転したとき、 その回転を右ねじの回転とみなして、右ねじの進む方向の単位ベクトル |
x,y,z各方向の単位ベクトルをそれぞれi,j,kとすると、
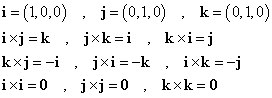
|
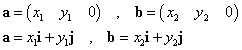
とすると、 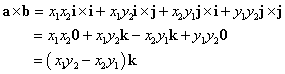
右辺は、a,bをそれぞれ行ベクトルとする2次の正方行列 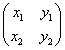 の行列式であるから、 の行列式であるから、
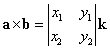
kは単位ベクトルであるから、 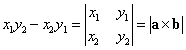
|
したがって、上の証明は、外積を用いれば、次のように書くことができる。
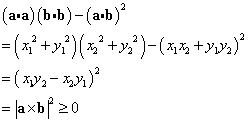
等号成立は、
|a|=0、すなわちa=o、または、
|b|=0、すなわちb=o、または、
sinθ=0 すなわち、θ=nπ (nは整数)、
すなわち、a,bが「1次従属」であるとき。
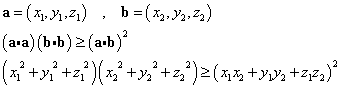
[証明]
3次元ベクトルについては、
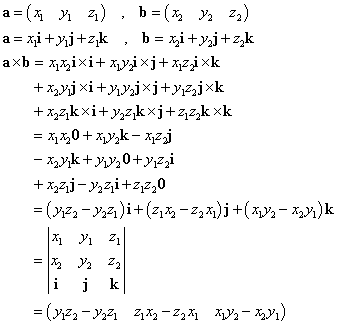
|
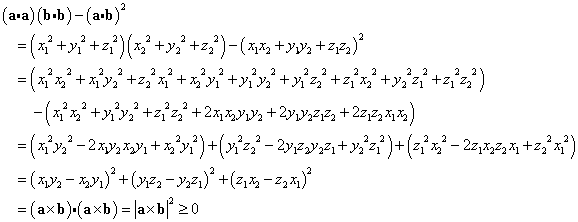
等号成立は、
|a|=0、すなわちa=o、または、
|b|=0、すなわちb=o、または、
sinθ=0 すなわち、θ=nπ (nは整数)、
すなわち、a,bが「1次従属」であるとき。
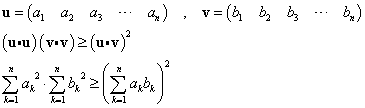
[証明1]
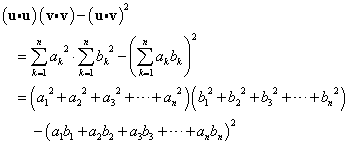
右辺は、
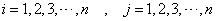 に対して、
に対して、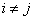 であるすべての組み合わせについて、
であるすべての組み合わせについて、
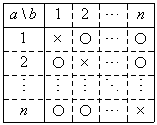
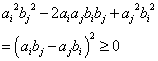
となるn(n-1)項をを加算したものであるから、正または0である。
等号成立は、すべての
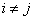 に対して、
に対して、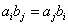 であるとき、
であるとき、
すなわち、
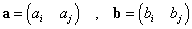 としたとき、
としたとき、
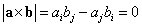
等号成立は、
|a|=0、すなわちa=o、または、
|b|=0、すなわちb=o、または、
a,bのなす角θに対してsinθ=0 すなわち、θ=nπ (nは整数)、
すなわち、a,bが1次従属であるときである。
[証明2]
- n=1のとき
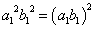 成立する。
成立する。
- n=mのとき
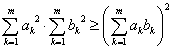
と仮定する。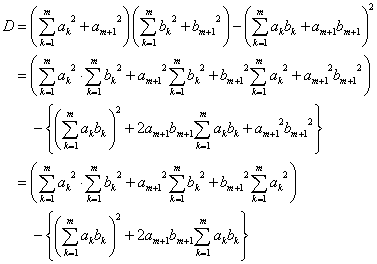
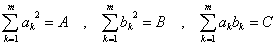 とおくと、仮定より
とおくと、仮定より 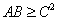
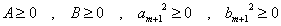
であるから、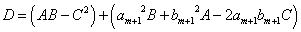 に対して、
に対して、
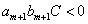 のとき、
のとき、 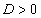
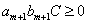 のとき、
のとき、
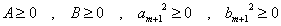
であるから、「相加平均・相乗平均の関係」より、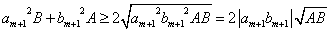
また、仮定より、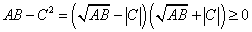
すなわち、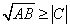
したがって、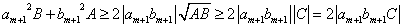
また、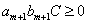 であるから、
であるから、
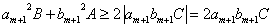
よって、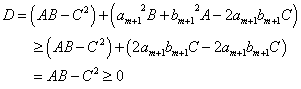
等号成立は、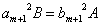 かつ、
かつ、 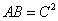
すなわち、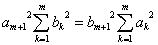 かつ、
かつ、 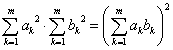
i,iiにより、任意の自然数nに対して成立する。
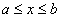 で連続な関数、f(x),g(x)に対して、
で連続な関数、f(x),g(x)に対して、
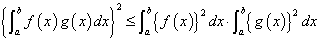
[証明]
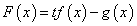
とおく。
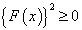
であるから、
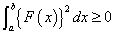
すなわち、
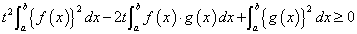
ここで、
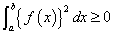
であるから、
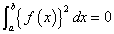 のとき
のとき
任意のxに対して、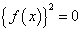 すなわち、
すなわち、 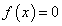 となるから、このとき、
となるから、このとき、
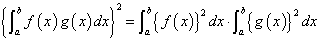
である。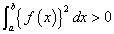 のとき
のとき