
(1)
立体V1の平面x=tによる切り口を想像すべく、いろいろな角度からの図面を作ってみた。
それぞれ右側の図面には、平面x=tが網目状に描き入れてある。
![]()
![]()
![]()
![]()
立体V1が、一番太くなるのは、弧ACのところであり、これが平面x=tを横切る場所で、断面の形状は劇的に変わるはずだ。
![]()
![]()
したがって、xy平面上の直線x=tと、直線ACすなわちx+y=0の交点(t,-t)を境に、場合わけをすることにする。
- 点P(t,s)が、直線ACのB側にいるとき、すなわち-t
 s
s 1のとき。
1のとき。
これをz軸の正の方向から見下ろしたのが、左の図、
- 点P(t,s)が、直線ACのD側にいるとき、すなわち-1
 s
s -tのとき。
-tのとき。
これをz軸の正の方向から見下ろしたのが、右の図、である。
![]()
![]()
P(t,s,0)を通るxy平面上の直線x+y=s+tを含み、z軸と平行な平面αを考え、
この平面αで、立体V1を切った断面は、円になる。これをB側から眺めたのが、下の図で、それぞれ、
を表している。このときP(またはP')を通りz軸と平行な直線が、円弧と交わる点Q(またはQ')のz座標が、平面x=tによる切り口の断面上の、y座標sに対応するz座標になる。これらの関係式を得ることが出来れば、それが、切り口の「図形」の式をあらわすことになるだろう。
- -t
 s
s 1のとき
1のとき
![]() |
この円の半径rは、
![]()
|
したがって、PQの長さは、
![]()
- -1
 s
s -tのとき
-tのとき
![]() |
この円の半径r'は、
![]()
|
したがって、P'Q'の長さは、
![]()
- x=t平面上に、(t,0,0)を原点として、それぞれy軸、z軸に平行に、Y軸、Z軸をとると、
立体V1の断面の形状は、下図のようになるだろう。(z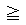 0のみを示した。)
0のみを示した。)
![]()
Y=-tのとき、![]()
![]()
よって求める面積をS1(t)とすると、
![]()
(2)
立体V2の、平面x=tによる切り口は、明らかに軸対象となるだろうから、下図のようになる。
2つの切り口の図形の共通部分に当たる面積をS(t)とすると、求める体積V1,V2の共通部分は、あきらかに、yz平面に関して対称であろうから、
![]()
となる。
![]()
![]()
したがって、求める体積は、
![]()


 s
s 1のとき。
1のとき。
 s
s -tのとき。
-tのとき。
 s
s 1のとき、
1のとき、
 s
s -tのとき、
-tのとき、
 s
s 1のとき
1のとき s
s -tのとき
-tのとき s
s 1のとき
1のとき
 s
s -tのとき
-tのとき
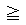 0のみを示した。)
0のみを示した。)