これは、次のような、「行ベクトル」、「正方行列」、「列ベクトル」の積として表現できる。
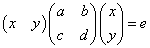 「結合法則」を用いれば、
「結合法則」を用いれば、
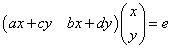 ,
, 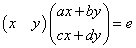
いずれの場合もこれは「行ベクトル」と「列ベクトル」の積、すなわち「内積」であって、その計算結果は「スカラー量」である。
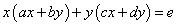
すなわち、
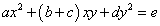
こうして、x2 , xy , y2の項、および定数項からなる2次曲線の式が得られた。
一方、まんなかにはさまれた「正方行列」が、「対角行列」である場合、
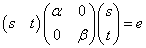
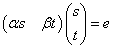 ,
, 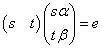
となるから、これはxyの項をもたない2次曲線であり、楕円、双曲線、または、2本の直線他・・・、を表現することが容易にわかる。
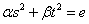
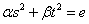 がst平面上で表す図形
がst平面上で表す図形
- α=β=0ならば、e=0 (s,t)任意。これは「全平面」を表す。
- α
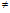 0 , β=0ならば、
0 , β=0ならば、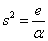
- e
 0ならば、このようなsは存在しない。
0ならば、このようなsは存在しない。
- e
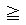 0ならば、
0ならば、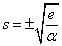 、これはs軸に垂直な直線である。
、これはs軸に垂直な直線である。
- e
- α=0 , β
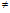 0ならば、
0ならば、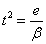
- e
 0ならば、このようなtは存在しない。
0ならば、このようなtは存在しない。
- e
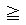 0ならば、
0ならば、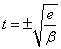 、これはt軸に垂直な直線である。
、これはt軸に垂直な直線である。
- e
- α
 0 , β
0 , β 0のとき。
0のとき。
- e=0ならば、
- α
 0,β
0,β 0・・・(s,t)=(0,0)原点
0・・・(s,t)=(0,0)原点
- α
 0,β
0,β 0・・・2直線
0・・・2直線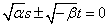
- α
 0,β
0,β 0・・・2直線
0・・・2直線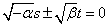
- α
 0,β
0,β 0・・・(s,t)=(0,0)原点
0・・・(s,t)=(0,0)原点
- α
- e
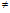 0ならば、
0ならば、
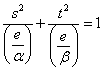
- α
 0,β
0,β 0,e
0,e 0または、
α
0または、
α 0,β
0,β 0,e
0,e 0のとき
0のとき
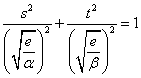 ・・・楕円
・・・楕円
- α
 0,β
0,β 0,e
0,e 0または、
α
0または、
α 0,β
0,β 0,e
0,e 0のとき
0のとき
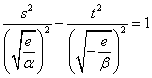 ・・・双曲線
・・・双曲線
- α
 0,β
0,β 0,e
0,e 0または、
α
0または、
α 0,β
0,β 0,e
0,e 0のとき
0のとき
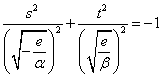 ・・・双曲線
・・・双曲線
- α
 0,β
0,β 0,e
0,e 0または、
α
0または、
α 0,β
0,β 0,e
0,e 0のとき
0のとき
このような(s,t)は存在しない。
- α
- e=0ならば、
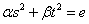 はs,tの1次の項をもたないから、放物線を表すことはない。
はs,tの1次の項をもたないから、放物線を表すことはない。
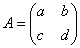 を
を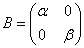 に関連付ける方法(対角化)、について考える。
に関連付ける方法(対角化)、について考える。
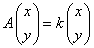 ただし
ただし 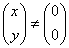 となる
となる
定数k(行列Aの固有値)、および定ベクトル
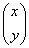 (固有値kに対応する固有ベクトル)
(固有値kに対応する固有ベクトル)
を求めたい。
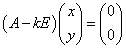 ただし
ただし 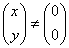
であるから、行列(A-kE)=
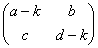 は逆行列をもたない。
は逆行列をもたない。
[証明]もし(A-kE)が逆行列をもつなら、これを両辺に左からかけて、
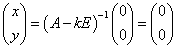
これは
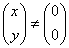 に反する。
に反する。
よって、(A-kE)は逆行列をもたない。
すなわち、
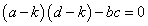
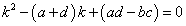 ・・・(1)
・・・(1)
これを行列Aの「固有方程式」と呼ぶ。この式は、下の「ハミルトン・ケーリーの定理」の式と係数の並びが等しい。
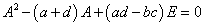
「固有方程式」、
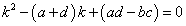 が異なる2実数解をもつ場合、すなわち、
が異なる2実数解をもつ場合、すなわち、
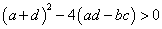
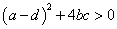
の場合について考える。
(1)の異なる2実数解をα,βとし、これらに対応する「固有ベクトル」をそれぞれ
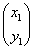 ,
,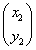 とすると、
とすると、
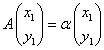 ,
, 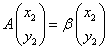
すなわち、
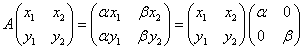
ここで、
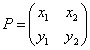
とおくと、α
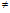 βであるから、
βであるから、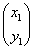 ,
,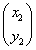 は互いに1次独立であり、したがってPは逆行列P-1をもつ。
は互いに1次独立であり、したがってPは逆行列P-1をもつ。
よって、AP=PBすなわち、P-1AP=B
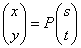 なる1次変換を見つけることができれば、
なる1次変換を見つけることができれば、
x2,y2の項と定数項以外に、xyの項を含む2次曲線の式を、
s2,t2と定数項のみの2次曲線の式に変換することができそうである。
ここで、
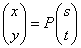 ならば、
ならば、
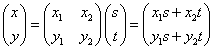
この「2次の正方行列」×「列ベクトル」、の式を、
「列ベクトル」×「2次の正方行列」、の式に書き換えると、
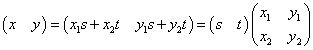
となり、2次の正方行列Pについて、主対角線成分以外の成分が上下入れ替わってしまっていることがわかる。
このような行列を「転置行列」と呼び、tPと書く。すなわち、
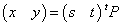
したがって、
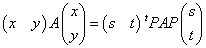
であり、ここでもし、tP=P-1であるような行列Pを得ることができれば、
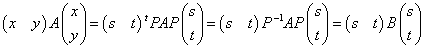
となり、目的は達成されるのである。
「直交行列」とは、どのような行列なのであろうか?
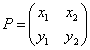 に対して、
に対して、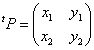
「直交行列」の定義から、
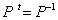 すなわち、
すなわち、
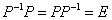 に対して、
に対して、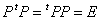 すなわち、
すなわち、
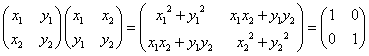
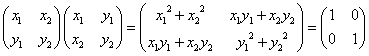
すなわち、
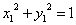 ・・・(1)
・・・(1)
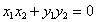 ・・・(2)
・・・(2)
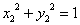 ・・・(3)
・・・(3)
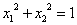 ・・・(4)
・・・(4)
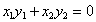 ・・・(5)
・・・(5)
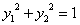 ・・・(6)
・・・(6)
(2)より、
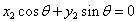 すなわち、
すなわち、
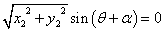 ただし、
ただし、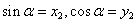
(3)より、
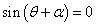
したがって、
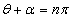 (ただし、nは整数)
(ただし、nは整数)
すなわち
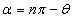
したがって、
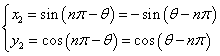
これはnが偶数の場合と、奇数の場合で異なち、
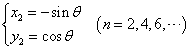 または、
または、 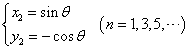
これらはいずれも、(4)(5)(6)を満たす。
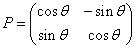
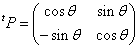
または、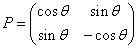
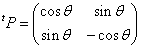
- のPは、原点周り反時計回りθ回転の1次変換を表す行列であり、
- のPは、
- まず、y軸対象に移動し、次に、原点まわり反時計回りθ回転を行う、という合成変換、
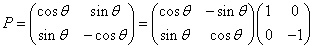
または、 - まず、原点まわり時計回りθ回転(反時計回り-θ回転)を行い、次に、y軸対象移動を行う、という合成変換、
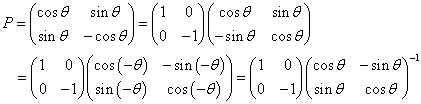
原点を通り、x軸とのなす角がθ/2である直線、すなわち、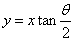 に関する対称移動の1次変換を表している。
に関する対称移動の1次変換を表している。
- まず、y軸対象に移動し、次に、原点まわり反時計回りθ回転を行う、という合成変換、
これで、「直交」の意味もよくわかる。この行列は、その2つの列ベクトルが、あるいは、その2つの行ベクトルが、互いに直交する単位ベクトルなのである。
互いに直交する単位ベクトルの組を、「正規直交基底」(「正規」とは長さ1のこと、「基底」とは互いに1次独立なベクトルの組のこと)といい、例えばxy座標平面では、(1,0),(0,1)という「正規直交基底」の1次結合で、すべての点をあらわしているのである。
- 対角行列Bに対して、(Aの固有方程式が異なる2実数解をもつならば、)
AP=PB
となるPを見つけることができる。 - さらに
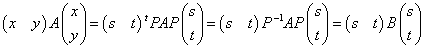
と変形できるためには、Pが「直交行列」でなければならず、
これは、Aの2つの固有ベクトルが、互いに直交する単位ベクトル(正規直交基底)であることを意味する。
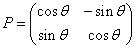 または、
または、 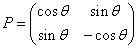 に対して、AP=PBであるから、
に対して、AP=PBであるから、
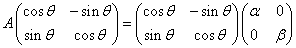 または、
または、 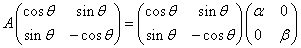
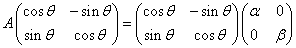 のとき のとき | 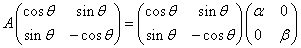 のとき のとき | |
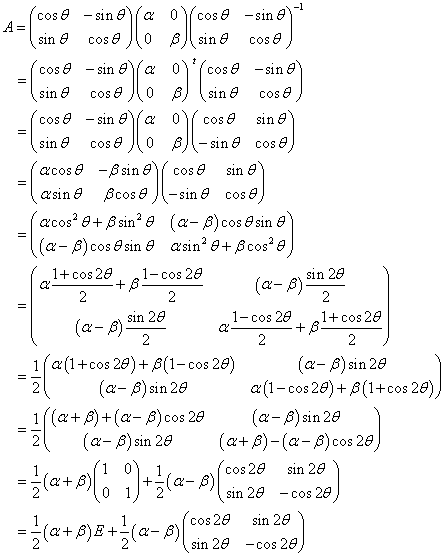 | 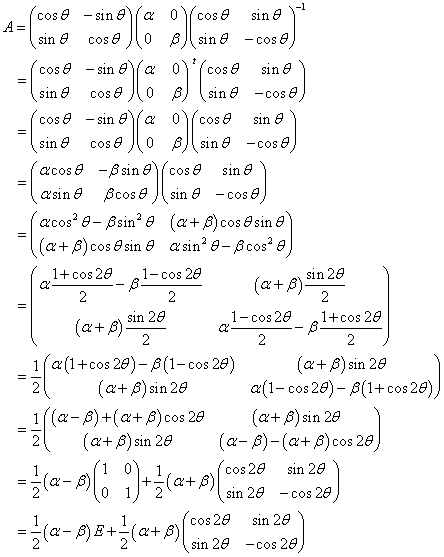 |
すなわち、
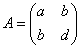
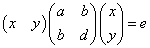
すなわち、
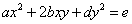
という、x2,y2の項と定数項以外に、xyの項を含む2次曲線の式を、
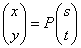 なる(「直交行列」による)1次変換を見つけることができれば、
なる(「直交行列」による)1次変換を見つけることができれば、
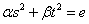
という、s2,t2と定数項のみのst平面上の2次曲線の式に変換することができ、
この式は、楕円、双曲線、2直線その他として、容易に作図することができる、ということであった。
したがって、逆に、定数a,b,dが与えられたときに、α,β,θが決定できなければならない。
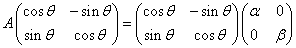 のとき
のとき
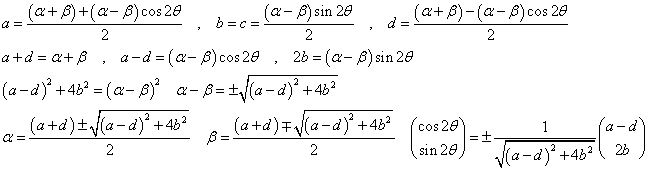
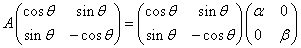 のとき
のとき
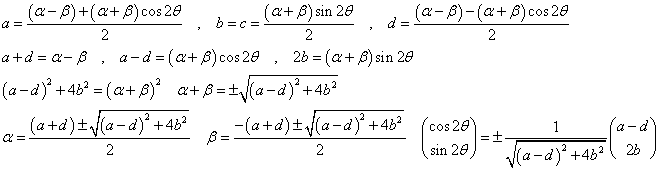
- [注]
ここで、実数a,b,dに対して、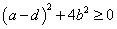 であり、
であり、
- 等号が成立するのは、a=dかつb=0である。
このときA=aEであるから、与えられた2次曲線は、ax2+ay2=eで、xyの項を含まず、そもそも変換する必要がない。 - したがって、
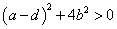 となり、Aの「固有方程式」が異なる2実数解α,βをもつ条件が満たされていることがわかる。
となり、Aの「固有方程式」が異なる2実数解α,βをもつ条件が満たされていることがわかる。
- 等号が成立するのは、a=dかつb=0である。