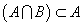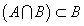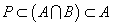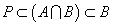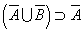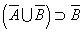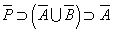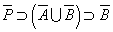---

1. [命題]  2以上の整数a,bに対して、
   

   P	→	Q
   ab-1が素数	ならば、	a=2であり、かつ、bは素数である

   [対偶]  2以上の整数a,bに対して、
   

   ¬Q	→	¬P
   a=2でないか、または、bは素数でない	ならば、	ab-1は素数でない

   ---

   • 「素数である」は、｢1とそれ以外に約数をもたな・い・｣と、否定文でしか定義できない言葉であるから、肯定文に転換しなければ証明できない。
   • 命題の結論部分を否定から肯定に転換するには、｢背理法｣と｢対偶｣のいずれも用いることができるが、条件部分を否定から肯定に転換するには、｢対偶｣しかない。
   
   
   

   		=
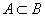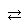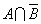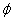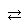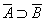   [命題]		[背理法]		[対偶]
   「AならばB」 が真である		Aであり、かつ、 Bでなければ、 矛盾が生ずる		「¬Bならば¬A」 が真である

   ---

   ここで、
   • P : a^b-1が素数であること
   • A : a=2であること
   • B : bが素数であること
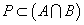   とすれば、証明したいのは、 である。ここで、
   • 
   • 
   であるから、
   • 
   • 
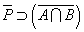   その｢対偶｣をとると、 、｢ド・モルガンの法則｣から、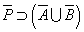
   
   
   
   
   
   さらに、
   • 
   • 
   であるから、
   • 
   • 
   すなわち、
   1. a=2でないならば、a^b-1が素数でないこと、かつ、
   2. bが素数でないならば、a^b-1が素数でないこと、
   を示せばよいことがわかった。

   ---

   [証明]
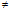   1. a2ならば、
      f(x)=x^b-1とおくと、
      f(1)=1^b-1=0であるから、
      f(x)は(x-1)で割り切れる。すなわち、a^b-1は(a-1)で割り切れる。
      ここで、bは2以上の整数であるから、a^b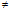a、すなわち、a^b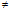-1a-1
      したがって、a^b-1はそれ自身以外の数a-1を因数にもつ。
      ここで、a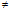2すなわち、a-1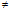1であるから、
      a^b-1はそれ自身と1以外の因数a-1をもつことになり、素数でないことが示された。
   2. bが素数でないならば、
      すなわちb=lmを満たす、いずれも1以外の正の整数l,mが存在する、ならば、
      a^b-1=a^lm-1は(a^l-1) , (a^m-1)を因数にもつ。

      ---

      なぜなら、
      • f(x)=x^m-1とおくと、f(1)=1^m-1=0であるから、f(x)は(x-1)で割り切れる。
        すなわち、a^lm-1は(a^l-1)で割り切れる。
      • g(x)=x^l-1とおくと、g(1)=1^l-1=0であるから、g(x)は(x-1)で割り切れる。
        すなわち、a^lm-1は(a^m-1)で割り切れる。

      ---

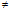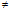      • l1 , m1であるから、a^l-1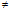1 , a^m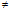-11

        ---

        なぜなら、もし、a^l-1=1 , a^m-1=1、すなわち、a^l=2 , a^m=2、ならば、これはa=2、かつ、l=m=1、のときに限られるからである。

        ---

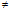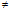      • l1 , m1であるから、a^l-1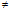a^lm-1 , a^m-1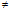a^lm-1
      よって、a^b-1はそれ自身と1以外の因数(a^l-1) , (a^m-1)をもつことになり、素数でないことが示された。
   
   
   
   
   
   
   
   
   
   

   ---

2. [命題]  2以上の整数a,bに対して、
   

   P	→	Q
   ab+1が素数	ならば、	b=2cとなる整数cが 少なくとも一つ、存在する

   [対偶]  2以上の整数a,bに対して、
   

   ¬Q	→	¬P
   いかなる整数cに対しても、 b=2cとならない	ならば、	ab+1は素数でない

   ---

   • さて、｢対偶｣をとったおかげで、｢素数である｣と言う｢否定文｣を回避することはできたが、条件部分¬Qが「いかなる整数cに対しても、
     b=2^cとならない」とあらたに｢否定文｣を含むようになってしまった。
     この部分を多少書き換えないと、大変扱いにくそうである。
     • Qは、「bは2以外の素因数を、決してもたない」という内容である。ならば、
     • ¬Qは、「bは2以外の素因数を、少なくとも一つ、もつ」になる。
   • ところで、f(x)=x^m+1に対しては、f(-1)=(-1)^m+1であるから、
     mが奇数のときのみ、f(x)が(x+1)で割り切れると断定できる。
     このロジックを使いたいので、「bは奇数を因数にをもつ」と、いいたい。
     2以外の素数はすべて奇数であるから、
     • ¬Q:「bは2以外の素因数を、少なくとも一つ、もつ」、は、
     • ¬Q:「bは1以外の奇数の因数を、少なくとも一つ、もつ」、と、
     書き換えてもよさそうである。無論、奇数には素数でないものも含まれるが、それらはすべて奇数の素数のみからなる合成数、であるから、
     • ¬Q:「bは1以外の奇数の因数を、少なくとも一つ、もつ」、ならば、
     • ¬Q:「bは奇数の素因数を、少なくとも一つ、もつ」、
     といえる。すなわち、
     • ¬Q:「bは1以外の奇数の因数を、少なくとも一つ、もつ」、は、
     • ¬Q:「bは奇数の素因数を、少なくとも一つ、もつ」、
     の｢十分条件｣である。そこで、証明すべき命題として、次の形を採用する。

   ---

   [対偶]  2以上の整数a,bに対して、
   

   ¬Q	→	¬P
   bは1以外の奇数の因数を、 少なくとも一つ、もつ	ならば、	ab+1は素数でない

   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   

   ---

   [証明]
   bは1以外の奇数の因数を、少なくとも一つ、もつから、
   正の整数l,mをもちいて、
   b=(2l+1)m
   と書くことができる。
   ここで、f(x)=x^2l+1+1とおくと、f(-1)=0であるから、f(x)は(x+1)で割り切れる。すなわち、
   (a^m)^2l+1+1は、a^m+1で割り切れる。
   • ここで、l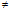0であるから、a^m+1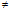(a^m)^2l+1+1
   • また、a^m+1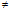0
   すなわち、(a^m)^2l+1+1は、1でもなく、それ自身でもない因数a^m+1をもつから、素数でない。
   すなわち、a^b+1は素数でない、ことが示された。