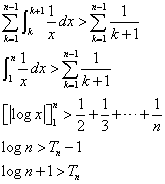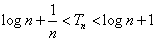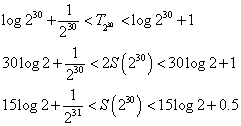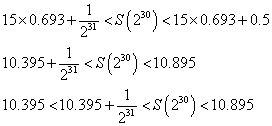n=1,2,3,・・・に対して、
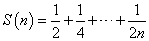
と定義する。
S(230)の整数部分を求めよ。ただし、loge2≒0.693147181を用いてよい。
プログラマの「性」であるが、まず、こんなもの、コンピュータに計算させればよかろ?、と思う。230=1073741824、ヨーロッパ風に3桁区切りすると、1,073,741,824、日本語なら、十億七千三百七十四万千八百二十四。
以下のわずか数行のBasicプログラムの、「for〜next」ループを、10億回以上繰り返すのである。半端な時間でないことは想像できる。現在、229を計算したところで、そろそろ20分くらい、になるか?、止まっている。
この入試問題を作った大学のスタッフの、「悪意」が、これで読み取れた(笑)。私が使っているこのコンピュータは、レノボの2014年春モデル、ワードもエクセルも何も入ってない空っぽの、最安値、4万円弱だが、intelプロセッサー搭載、パーソナルコンピュータとしては、現時点で「最速」のはずなのだ。演算に使用しているアプリケーションは、新潟大学の教授がフリーウェアとして提供してくださっている、「Tiny_Basic」、
つまり、素人がお金をかけずに、確かめてみることができるS(229)をたった一つ越えるだけで、あんたたちは、どうせ、もっと演算速度の速い「スーパー・コンピュータ」を使えるんでしょ?、それでこっそり確認したうえで、こんなく・だ・ら・な・い・入試問題作ったんでしょ?、と、「義憤」を振りまいていたとところ、おや?、答えが返ってきた(笑)。S(230)の、整数部分は、「10」のようである。

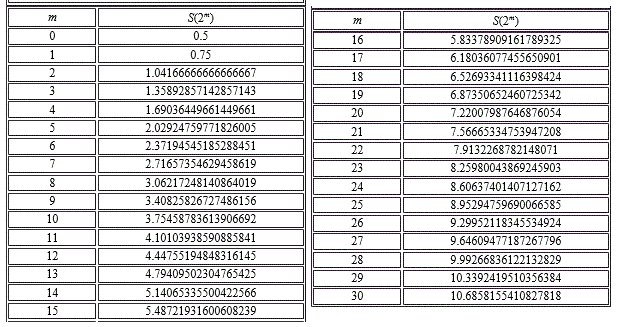
では、仕方ない(笑)、S(230)の、整数部分が10であること、ほかならぬ10でしかありえないこと、を、機械の力を借りずに「証明」しなければならない。次回期待。
前回、Basicで計算してみたS(2m)の値を、横軸mでグラフにしてみて、びっくりした。単調増加であることはもちろん、ほぼ、正比例ではないか?、ここでは、n=2m、すなわち、m=log2n、つまり横軸は、「対数目盛」になっているから、実・際・の・(笑)増加は、もっともっと遅い。0.5から始まって、約10億項まで足してやっと10なのである。
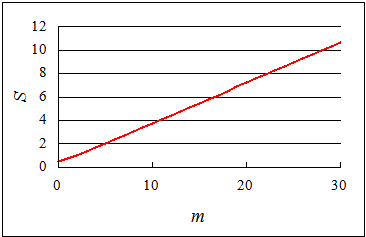
この数列、前も出てきたが、いわゆる「調和数列」をただ半分にしただけのものだが、その和は一般的に表式できないことが知られている。それでも、+∞に発散することは、ちょっとした技巧を用いて証明できるらしい。吉田武「オイラーの贈り物」(ちくま学芸文庫)に紹介してあった。あまりにも増加が遅いので、なかなか常識的には、「発散」しそうにも思えないのだが、なるほど、こうして横軸を対数目盛で見ると、頷けるから、驚いたのだ。
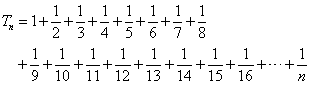
この調和数列の第2項以降を、項数2l、ただしl=0,1,2,・・・の「群」に分割していく。
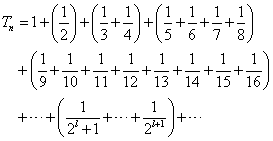
各「群」については、次のような不等式が成り立つ。
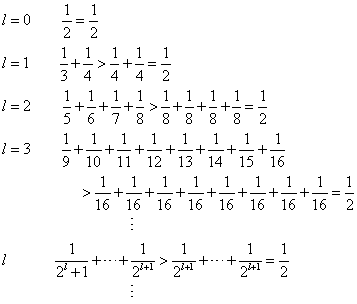
したがって、
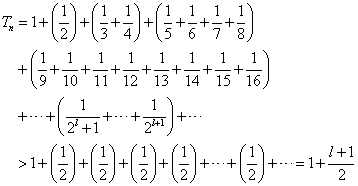
ここで、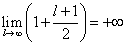 だから、無限大より「でかい」ものは、また無限大であるから(笑)、調和数列の和Tnもまた、発散するのである。
だから、無限大より「でかい」ものは、また無限大であるから(笑)、調和数列の和Tnもまた、発散するのである。
では、S(230)の整数部分が10であることの証明に取り掛かろう。高校数学の数学IIIの教科書の一項目、「定積分と不等式」、タイトルだけ聞くと何が言いたいのか一向に判らないテーマに関係している。
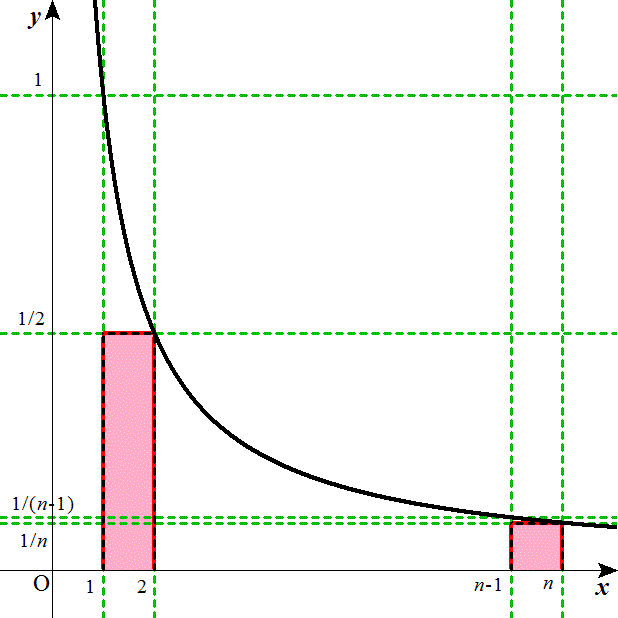
f(x)=x-1という関数を、x>0の範囲で考えると、グラフは以下の如く「反比例」のグラフで、全区間単調減少である。
横軸の目盛を、自然数kで切り分けていくと、「単調減少」であることから直ちに、
任意のkに対して、f(k)>f(k+1)
と言える。下の図で、
- 直線x=k、x=k+1、y=f(k)、y=0(x軸)、で囲まれた長方形、ライトブルー■とピンク■の部分の合計、の面積は、
f(k)×{(k+1)-(k}=f(k)
- 直線x=k、x=k+1、と、曲線f(x)=x-1、そしてx軸、で囲まれた部分の面積、
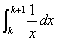
- 直線x=k、x=k+1、y=f(k+1)、y=0(x軸)、で囲まれた長方形、ピンク■の部分のみ、の面積は、
f(k+1)×{(k+1)-(k}=f(k+1)
これら三者の間には、次の不等式が成り立つ。
f(k)>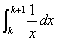 >f(k+1)
>f(k+1)
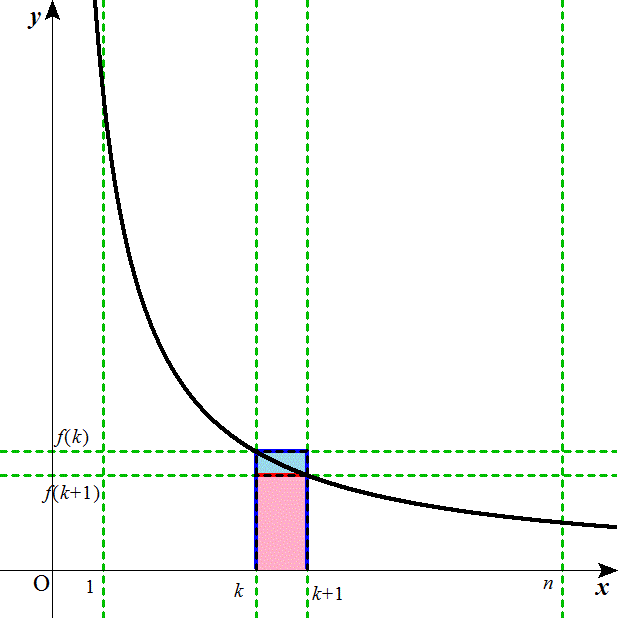
ならば、
- まず、
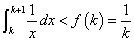 から、これを、k=1から、k=n-1まで加算して、
から、これを、k=1から、k=n-1まで加算して、
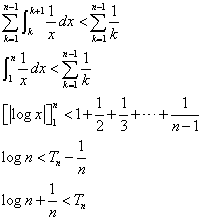
が得られる。下の図の、すみれ色■より、ライトブルー■が、大きい、という意味だ。
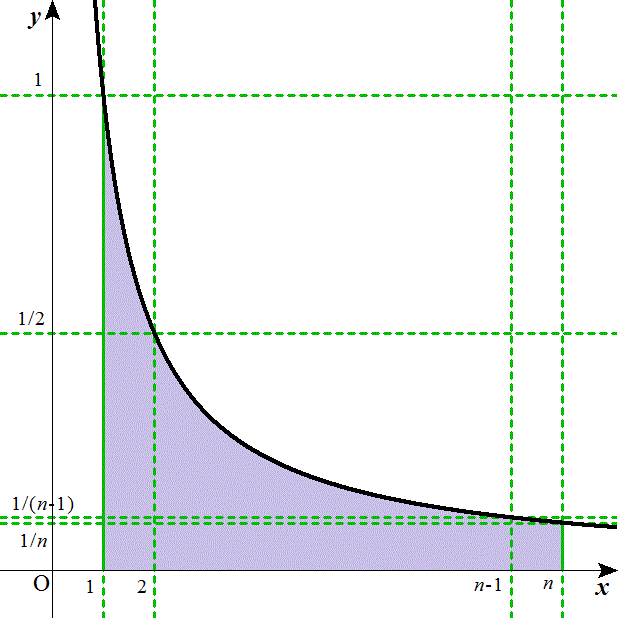
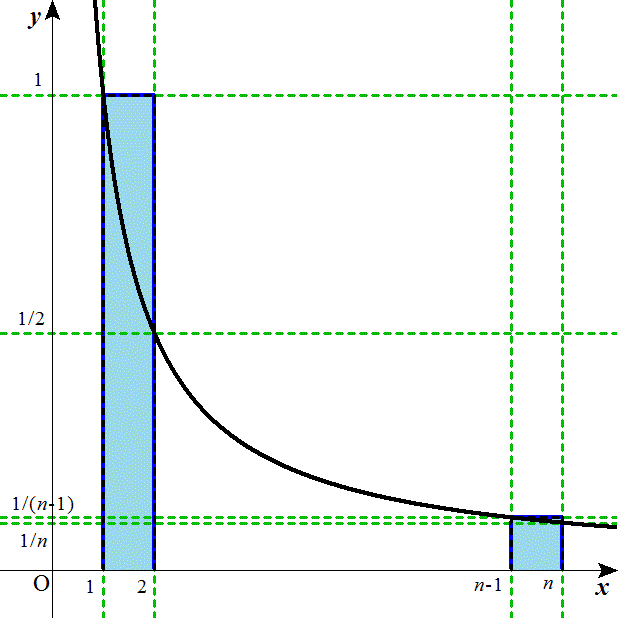
- 次に、
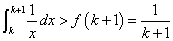 から、これを、k=1から、k=n-1まで加算して、
から、これを、k=1から、k=n-1まで加算して、
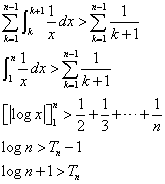
が得られる。下の図の、すみれ色■の方が、ピンク■より、大きい、という意味だ。

i,iiから、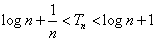
ここに、n=230を代入すると、S(n)=2Tnであるから、
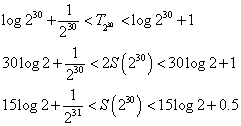
log2≒0.693として、
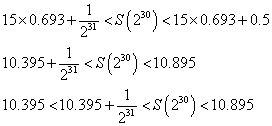
なるほど、S(230)の整数部分は、10であることが、示されたのである。
ところで、前回、この数列の和を、横軸、対数軸で見るとまるで正比例みたい!、という驚くべき事実を発見したのだが、では、対数目盛ではなくそのままnを横軸にしたら、どんなグラフだろう?、と考え、やってみた。Excel、いや、その「バッタもん」のKin●Softスプレッドシート、であるが、n=1000まで計算してもらったのである。なるほど、発散はものすごく遅く、いかにも、ひょっとしたら、どこかに収束するのでは?、と思わせるくらいのものだろ?
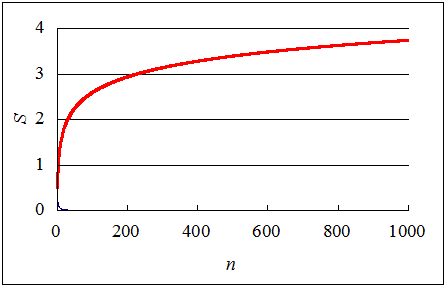
そうか!、後から気づいた。今度はこのグラフ、対数関数じゃない?、調和数列の和、連続変数化すれば、対数関数になる、ならば、横軸を対数目盛にとれば、直線になる!、なるほど、理の当然、であった(笑)。
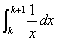
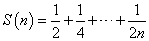



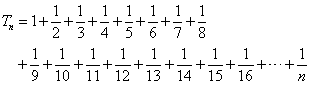
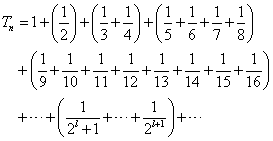
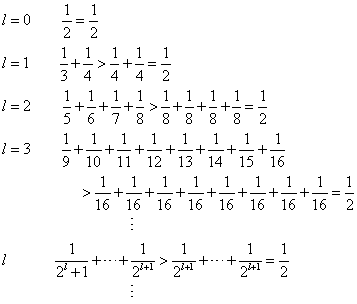
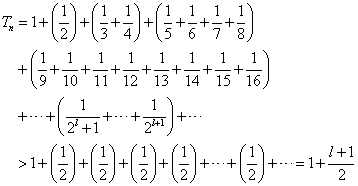
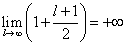 だから、無限大より「でかい」ものは、また無限大であるから(笑)、調和数列の和Tnもまた、発散するのである。
だから、無限大より「でかい」ものは、また無限大であるから(笑)、調和数列の和Tnもまた、発散するのである。
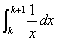
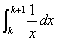 >f(k+1)
>f(k+1)

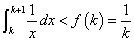 から、これを、k=1から、k=n-1まで加算して、
から、これを、k=1から、k=n-1まで加算して、
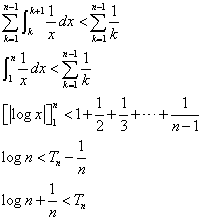


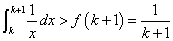 から、これを、k=1から、k=n-1まで加算して、
から、これを、k=1から、k=n-1まで加算して、