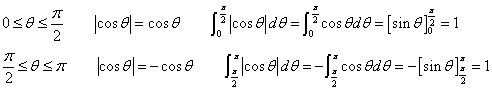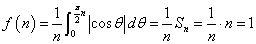第3問

琉球大学(理系)2009、第3問
- 問1
部分積分、
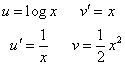
により、
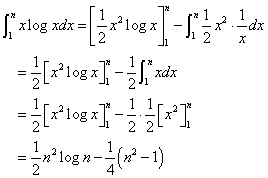
- 問2
f(x)=xlogxとおくと、
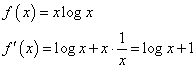
であるから、x≧e-1で、f(x)は単調増加、
したがって、x≧1で、f(x)は単調増加、
よって、k=1,2,3,・・・、に対して、
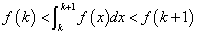
すなわち、
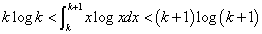
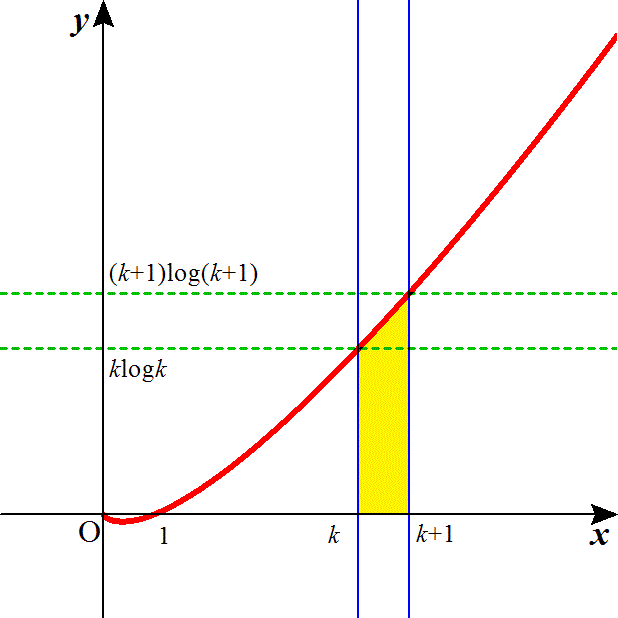
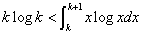 ・・・(1)
・・・(1)
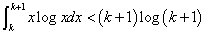 ・・・(2)
・・・(2)
(1)より、
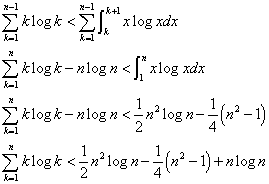
(2)より、
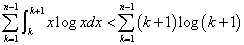
ここで右辺に、m=k+1なる変数変換をほどこすと、
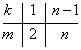
であるから、
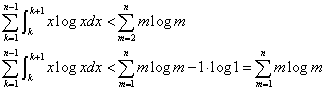
ふたたび変数をkに戻し、
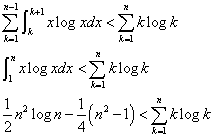
よって、示された。
- 問3
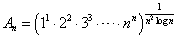
とおくと、
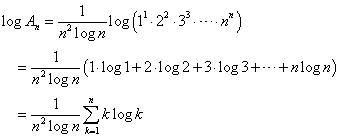
問2の結果より、
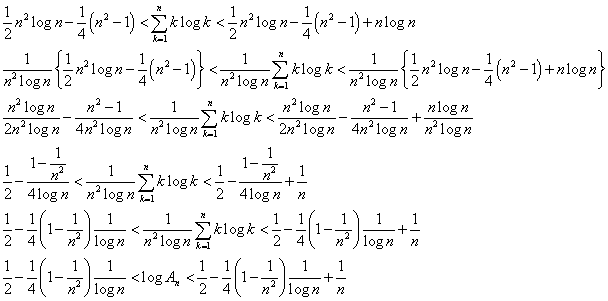
ここで、
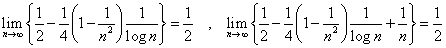
であるから、「はさみうちの原理」より、
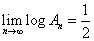
したがって、
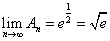
第2問

琉球大学(理系)2009、第2問
- 問1
以下のような置換積分によって、
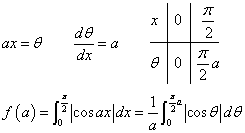
ここで、
0<a<1だから、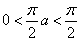
したがって、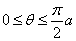 に対して、|cosθ|=cosθ
に対して、|cosθ|=cosθ
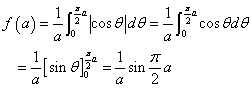
- 問2
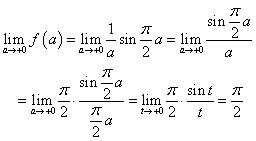
ここでは、πa/2=tなる変数変換をほどこし、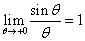 を用いた。
を用いた。
- 問3
上と同様の置換積分により、自然数nに対して、
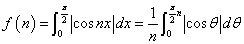
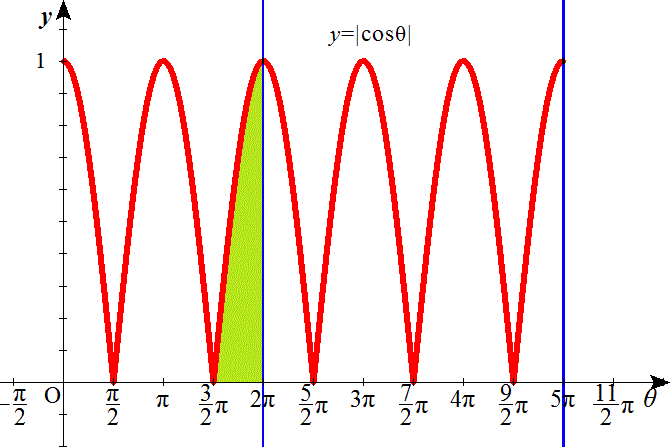
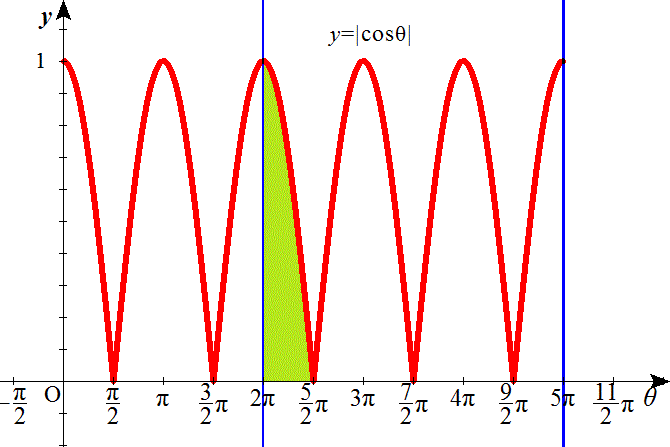
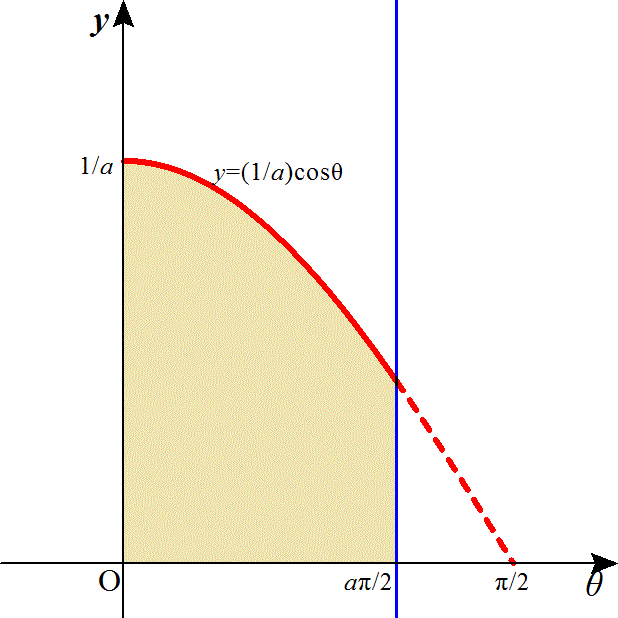
ここで、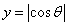 のグラフを描いてみると、
のグラフを描いてみると、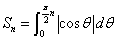 は、以下の色を付けた部分の面積である。
は、以下の色を付けた部分の面積である。
| nが偶数のとき(n=10) | nが奇数のとき(n=11) |
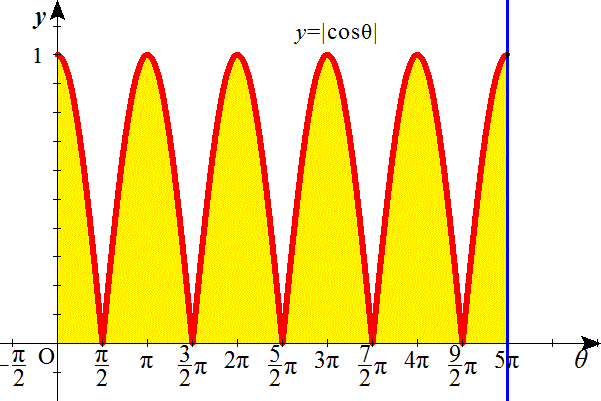 | 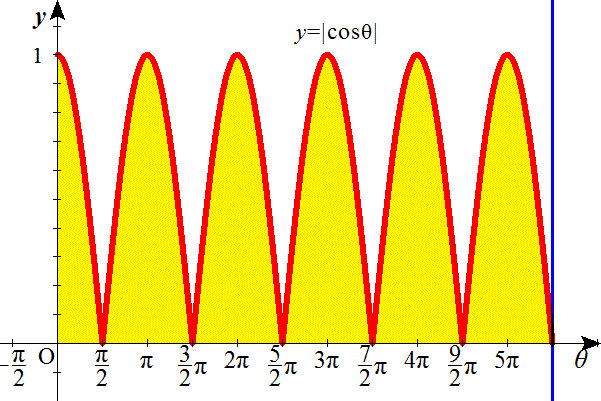 |
ところで、
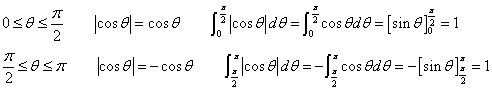
であるから、下図の色を付けた部分の面積は、1であり、
曲線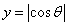 下の面積
下の面積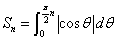 は、nが偶数であるか奇数であるかにかかわらず、n×1であることがわかる。
は、nが偶数であるか奇数であるかにかかわらず、n×1であることがわかる。
よって、
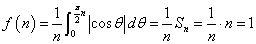
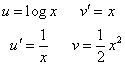
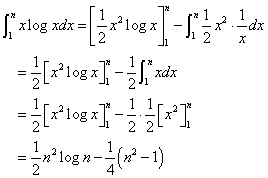
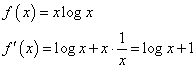
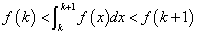
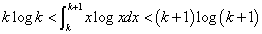

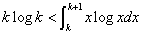 ・・・(1)
・・・(1)
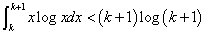 ・・・(2)
・・・(2)
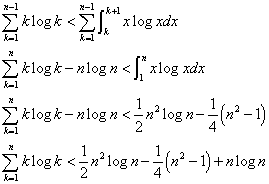
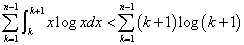
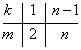
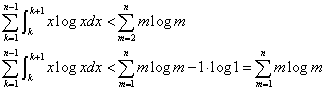
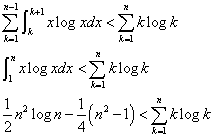
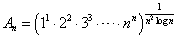
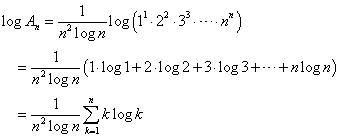
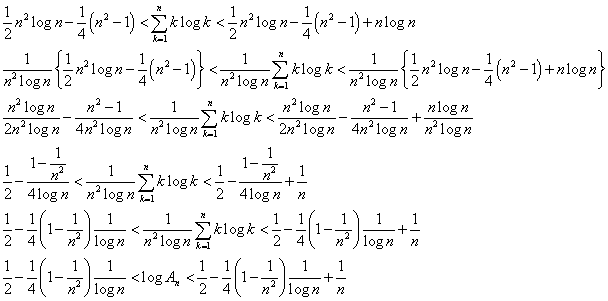
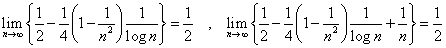
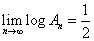
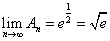


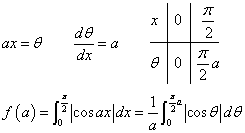
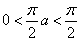
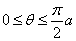 に対して、|cosθ|=cosθ
に対して、|cosθ|=cosθ

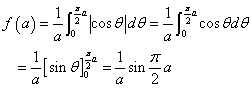
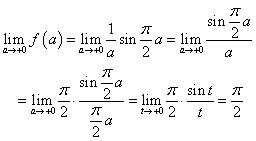
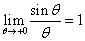 を用いた。
を用いた。
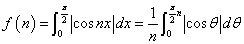
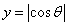 のグラフを描いてみると、
のグラフを描いてみると、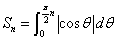 は、以下の色を付けた部分の面積である。
は、以下の色を付けた部分の面積である。