「大きさ」と「方向」のみを要素とするもの。では、「大きさ」と「方向」以外にどんな要素がありうるのかというと、たとえば「位置」。つまり、ベクトルは「位置」には拘束されない。どこへでも、その「大きさ」と「方向」を変えない限り、つまり、平行移動によって、動かすことができる。というより、「移動」という概念がない。だから、平行移動によって「重なり合う」ベクトルは、すべて「同じ」ベクトルである。
従って、二つのベクトルが「等しい」ということ(相等性)は、「平行移動によって重ねられること」と、定義される。
「ベクトルでないもの」にはどんなものがあるだろうか?「量」のみを要素とするものを「スカラー」という。「量」と「大きさ」はどこが違うのかというと、「大きさ」はその定義上「負」の量を含まない。「量」が任意の実数値を取ることができるとすれば、それは当然「負」の量も含む。ベクトルでは、「方向」が180度隔たっているといえば反対向きの量を示せるから、「負」の「大きさ」を持ち込む必要がない。とすれば、「スカラー」は「正」と「負」を唯一の「方向」とする量だといえる。
従って「スカラー」は、1次元の数直線に対応付けることができる。「1次元」とは、ただ一つの、正負を含む実数値によって、その場所が特定できることを意味する。
これに対して、平面が「2次元」と呼ばれるのは、たとえば(x,y)座標では、(x,y)という二つの実数値の組み合わせで、その平面に含まれるすべての点が、もれなく表現できるからである。
さらに、空間が「3次元」と呼ばれるのは、たとえば(x,y,z)座標では、(x,y,z)という三つの実数値の組み合わせで、その空間に含まれるすべての点が、もれなく表現できるからである。
| 平面内の任意の点を表す位置ベクトルは、2個の「1次独立」なベクトルの、「1次結合」によって、ただ「一通りに(一意的に)」、表現できる。 |
- 1次独立性:いずれも零ベクトルでなく、かつ、互いに平行でない2個のベクトルを、互いに1次独立であるという。
「1次独立」の反対語は「1次従属」であって、これは、「一方のベクトルが、他のベクトルの1次式によって表現できること」を意味する。
たった2個のベクトルで、「一方のベクトルが、他のベクトルの1次式によって表現できること」といえば、それは「定数倍」しかありえない。もしくは、一方が零ベクトルであるならば、それは他方がどのようなベクトルであったとしても、その「ゼロ倍」として、「表現できる」から、これも「1次従属」である。
もう一つ別の言い方をすると、
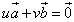
という式があったとき、- ベクトルaとベクトルbがいずれも零ベクトルならば、u,vはまったく任意である。
- ベクトルaが零ベクトルで、ベクトルbが零ベクトルでないならば、v=0だが、uは任意である。
同様に、ベクトルbが零ベクトルで、ベクトルaが零ベクトルでないならば、u=0だが、vは任意である。 - ベクトルa、ベクトルbがいずれも零ベクトルでなく、互いに平行だとしたら、
 は
は のk倍(k≠0)とかけるから
のk倍(k≠0)とかけるから
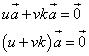
となり、 ≠
≠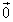 であるから、
であるから、
u+vk=0
k≠0だから、v=-u/k
とかける。このような関係を満たすu,vは(0以外に)無数に存在する。 - 最後に、ベクトルa、ベクトルbがいずれも零ベクトルでなく、互いに平行でもないとしたら、この式を満たす u,vは、u=v=0しかありえない。
2個のベクトルの「1次従属」性
- [表現1]いずれか一方のベクトルが、他方の1次式(定数倍)で表現できること。
- [表現2]少なくとも一方のベクトルが、零ベクトルであるか、または互いに平行であること。
- [表現3]2個のベクトル
 と
と が1次従属であるとは、
が1次従属であるとは、
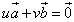 を満たす定数u,vがu=v=0以外にも存在することである。
を満たす定数u,vがu=v=0以外にも存在することである。
従って、「1次独立」とは、「1次従属」の「否定」であるから、2個のベクトルの「1次独立」性
- [表現1]いずれのベクトルも、他方の1次式(定数倍)で表現できないこと。
- [表現2]いずれのベクトルも、零ベクトルでなく、かつ互いに平行でないこと。
- [表現3]2個のベクトル
 と
と が1次独立であるとは、
が1次独立であるとは、
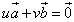 を満たす定数u,vがu=v=0以外に存在しないことである。
を満たす定数u,vがu=v=0以外に存在しないことである。
- 1次結合:のちに述べるように、2個のベクトルの「演算」には、「加法・減法」、「掛け算」として「定数倍・内積・(外積)」があるが、このうち、「加法・減法」と「定数倍」の組み合わせのみで、表現された式のことを「1次結合」と呼んでいる。
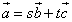
変数x,yに対して、ax+byを「1次式」と呼ぶことからのアナロジー(類比)であろう。 - 「平面内の任意の点を表す位置ベクトルは、2個の『1次独立』なベクトルの、『1次結合』によって、ただ『一通りに(一意的に)』、表現できる。」とは、「証明」を要しない、「公理」なのだろうか?
たとえば点(3,4)は、明らかに「1次独立」な(1,0)と(0,1)を用いて、その3倍と4倍の和であり、それ以外ではありえないというのは、自明のことに思われる。原点から、(3,4)に直線的に移動する方法は、右に3上に4隔たった点に移るただ一つの方法しかない。これはおそらく、「ユークリッド幾何学」の「2点を通る直線はたった1本しか存在しない」という「公理」と同値なのだと思われる。 - ちなみに、[表現3]は、1次独立なベクトルa,ベクトルbで「原点」を表現する方法が一つしかないことを意味している。
| 空間内の任意の点を表す位置ベクトルは、3個の「1次独立」なベクトルの、「1次結合」によって、ただ「一通りに(一意的に)」、表現できる。 |
- 1次独立性:
- いずれも0ベクトルでなく、
- かつ、3個のうちどの2個も互いに平行でなく、
- かつ、同一平面上にない、
ここでも「1次独立」の反対語は「1次従属」であって、これは、「いずれか一つのベクトルが、他の二つのベクトルの1次式によって表現できること」を意味する。
ここでも、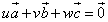
について考える。- 3個のベクトルがいずれも零ベクトルならば、u,v,wはまったく任意である。
- 3個のベクトルのうち、2個のベクトルたとえばベクトルaと、ベクトルbが零ベクトルであり、残り1個のベクトルcが零ベクトルでないならば、w=0だが、u,vは任意である。
他の場合も同様。 - 3個のベクトルのうち、どれか1個だけが零ベクトルで、他の2個は零ベクトルでないとき、たとえば、ベクトルaのみが零ベクトルであるとき、
- ベクトルb、ベクトルcが平行ならば、これらが「1次従属」なので、v=w=0でないv,wが存在する。また、uは任意である。
- ベクトルb、ベクトルcが平行でないならば、これらが「1次独立」なので、v=w=0であるが、uは任意である。
- 3個のベクトルの、いずれもが零ベクトルでないとき、
- 3個がすべて平行だとしたら、
 は
は のk1倍(k1≠0)、
のk1倍(k1≠0)、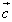 は
は のk2倍(k2≠0)とかけるから、
のk2倍(k2≠0)とかけるから、
(u+k1v+k2w) =
=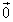
となり、 ≠
≠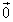 であるから、
であるから、
u+k1v+k2w=0
これを満たす(u,v,w)=(0,0,0)以外の(u,v,w)の組み合わせは、無数に存在する。たとえば、(u,v,w)=(0,-k2,k1)など。 - 3個のうちいずれか2個のみが平行だとしたら、たとえば
 と
と が平行で、これらは
が平行で、これらは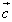 とは平行でないとすれば、
とは平行でないとすれば、 は
は のk倍(k≠0)とかけるから、
のk倍(k≠0)とかけるから、
(u+kv) +w
+w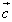 =
=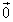
上で述べた「平面ベクトルの1次独立性」から、u+kv=0かつ、w=0
これを満たす(u,v,w)=(0,0,0)以外の(u,v,w)の組み合わせは、無数に存在する。たとえば、(u,v,w)=(-k,1,0)など。
他の場合も同様。 - 3個のベクトルがいずれも互いに平行でないが、同一平面上にあるとき、
上で述べた「平面ベクトルの1次独立性」から、ベクトルcは1次独立な2個のベクトルaとベクトルbの1次結合で表すことができる。
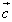 =k1
=k1 +k2
+k2 (ただし、k1≠0かつk2≠0)
(ただし、k1≠0かつk2≠0)
したがって、
(u+k1w) +(v+k2w)
+(v+k2w) =
=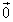
ふたたび「平面ベクトルの1次独立性」から、u+k1w=0かつv+k2w=0
これを満たす(u,v,w)=(0,0,0)以外の(u,v,w)の組み合わせは、無数に存在する。たとえば、(u,v,w)=(-k1,-k2,1)など。
- 3個がすべて平行だとしたら、
- 最後に、3個のベクトルa、ベクトルb、ベクトルcがいずれも零ベクトルでなく、どの2個も互いに平行でなく、かつ、3個が同一平面上にもないとしたら、この式を満たす u,v,wは、u=v=w=0しかありえない。
3個のベクトルの「1次従属」性
- [表現1]3個のうちいずれか一つのベクトルが、他の二つのベクトルの1次式(1次結合)によって表現できること。
- [表現2]3個のうち少なくとも1個のベクトルが、零ベクトルであるか、または、少なくともいずれか2個のベクトルが互いに平行であるか、または、3個のベクトルが同一平面上にあること。
- [表現3]3個のベクトル
 ,
, ,
,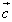 が1次従属であるとは、
が1次従属であるとは、
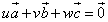 を満たす定数u,v,wがu=v=w=0以外にも存在することである。
を満たす定数u,v,wがu=v=w=0以外にも存在することである。
従って、「1次独立」とは、「1次従属」の「否定」であるから、3個のベクトルの「1次独立」性
- [表現1]3個のうちいずれの一つのベクトルも、他の二つのベクトルの1次式(1次結合)によっては表現できないこと。
- [表現2]3個のうちいずれの1個のベクトルも、零ベクトルでなく、かつ、3個のうちいずれの2個のベクトルも互いに平行でなく、かつ、3個のベクトルが同一平面上にないこと。
- [表現3]3個のベクトル
 ,
, ,
,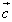 が1次独立であるとは、
が1次独立であるとは、
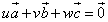 を満たす定数u,v,wがu=v=w=0以外に存在しないことである。
を満たす定数u,v,wがu=v=w=0以外に存在しないことである。
- 1次結合:「加法・減法」と「定数倍」の組み合わせのみで、表現された式のことを「1次結合」と呼ぶ。
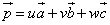
- ちなみに、[表現3]は、1次独立なベクトルa,ベクトルb,ベクトルcで「原点」を表現する方法が一つしかないことを意味している。
|
- 加法
 +
+ =
= ・・・①
・・・①
 +
+ +
+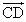 =
=
・・・・
これは、経路によらずに、「始点」と「終点」によってベクトルが決定されることを意味している。 - 減法
ベクトルは「大きさ」と「方向」の2つの要素を持っているから、「大きさ」が同じで「方向」が逆のベクトルは、「マイナス」をつけることで表現できる。
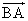 =-
=-
したがって、①は、
 -
-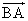 =
=
と書ける。移項すると、
 =
= -
-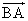
この式は、「左辺:始点Aで表現されたベクトル」を「右辺:始点Bで表現されたベクトル」に書き換えるには、元の「終点」からもとの「始点」を「引けばよい」ことを表している。これを「始点のつけかえルール」と呼んでおく。
ベクトルの「矢印」を「主体・観測者」から「対象」へ向かった「視線」だと考えれば、別の「観測者」から眺めた「対象」は、かつての「観測者」の「視線」から、そのかつての「観測者」の要素を除去すればよいことになる。これは立派な「相対性理論」である。 - 乗法
「大きさ」と「方向」という2つの要素を持つベクトルの特性から、さまざまな「乗法」が考えられる。次の3つが定義されている。ひとつは、「ベクトル」と「スカラー」の積、あとの2つは「ベクトル」と「ベクトル」の積である。- スカラー倍(定数倍)
ベクトルには「大きさ」と「方向」の2つの要素があるが、「方向」をそのままに「大きさ」だけを定数倍するには、ベクトル自体を定数倍すればよい。定数が負の値を持つときは、上の「減法」で述べたように、逆向きのベクトルと考えることができる。
 =k
=k
- スカラー積(内積)
ベクトルとベクトルの掛け算のうち、計算結果がスカラーとなるもの。
 ・
・
 =|
=| ||
|| |cosθ
|cosθ
ここで、| |はベクトルaの「大きさ」、θはベクトルaとベクトルbの「なす角」を表す。
|はベクトルaの「大きさ」、θはベクトルaとベクトルbの「なす角」を表す。
同じベクトルa同士の内積は、θ=0であるから、
 ・
・
 =|
=| |2
|2
また、上の「始点つけかえルール」を用いれば、 =
= -
- であるから、
であるから、
 ・
・
 =(
=( -
- )・(
)・( -
- )
)
内積にはその定義上「交換法則」「分配法則」が成り立つから、
 ・
・
 =(
=( -
- )・(
)・( -
- )
)
= ・
・ -2
-2 ・
・
 +
+ ・
・
=| |2-2|
|2-2| ||
|| |cosθ+|
|cosθ+| |2
|2
ここでθは∠BACであり、この式は「余弦定理」を表している。
[物理学上の適用場面]
・「仕事」の定義:「仕事(スカラー量)」は「力(ベクトル量)」と「変位(ベクトル量)」の内積である。 - (*)ベクトル積(外積)
ベクトルとベクトルの掛け算のうち、計算結果がベクトルとなるもの。
 ×
×
 =(|
=(| ||
|| |sinθ)
|sinθ)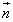
ここでベクトルnは、「ベクトルaをベクトルbに重ねようと回転させたとき、その方向に回転させた右ねじが進む方向の単位ベクトル(大きさが1のベクトル)」と定義される。従って外積には交換法則が成り立たない。
[物理学上の適用場面]
・「力のモーメント」、「面積速度」、「フレミングの左手の法則」など。
- スカラー倍(定数倍)
-
平面上に、同一直線上にない3点O,A,Bがあったとしよう。この3点を結べば「三角形」ができるが、これは2個のベクトル
 ,
, が、ちゃんと「大きさ」を持ち、違う「方向」を向いている、まさに「1次独立」であることを意味している。
が、ちゃんと「大きさ」を持ち、違う「方向」を向いている、まさに「1次独立」であることを意味している。
つまり「1次独立」な2個のベクトルで作られるもっともシンプルな図形が、三角形なのだ。
ところで、上で述べたように、2次元平面上の、任意の点は、1次独立な2個のベクトルの1次結合で、ただ一通りに表現できる。
たとえば点Pは2個の1次独立なベクトル ,
, を用いて、次のように表され、
を用いて、次のように表され、
 =s
=s +t
+t
点Qも同様に、2個の1次独立なベクトル ,
, を用いて、次のように表されたとしよう。
を用いて、次のように表されたとしよう。
 =u
=u +v
+v
これらの内積を計算すると、
 ・
・ =su
=su ・
・ +(sv+tu)
+(sv+tu) ・
・ +tv
+tv ・
・
という風に、平面上のどのようなベクトルであったとしても、2個のベクトルの内積の計算過程には、 ・
・ ,
, ・
・ ,
, ・
・ の、たった3種類の項しか出てこないことがわかる。
の、たった3種類の項しか出てこないことがわかる。
 ・
・ は辺OAの長さの2乗である。
は辺OAの長さの2乗である。
 ・
・ は辺OBの長さの2乗である。
は辺OBの長さの2乗である。
 ・
・ は辺OA,OBの長さにそのなす角のコサインをかけたものである。
は辺OA,OBの長さにそのなす角のコサインをかけたものである。
したがって、これら3個の内積の値が「わかっている」ということは、「2辺とその間の角(2辺挟角)」が「わかっている」ということであって、これは△OABが「確定」していることを意味する。無数に存在するはずのさまざまな三角形の中で、ただ一つの「特定の」三角形と「合同」であるといえるからだ。平面上の2個の1次独立なベクトルを、  ,
, とすると、
とすると、
- これらの1次結合で、平面上のすべてのベクトルを表現でき、
- これらの2個のベクトルから作られる「3種類の内積の値」、
 ・
・ ,
, ・
・ ,
, ・
・ がわかっていれば、その平面上のどのような点であったとしても、それらを結んでできる「線分の長さ」や、「線分同士のなす角」をすべて、計算することができる。
がわかっていれば、その平面上のどのような点であったとしても、それらを結んでできる「線分の長さ」や、「線分同士のなす角」をすべて、計算することができる。
-
話を空間に拡張すると、3個の1次独立なベクトル
 ,
, ,
, で作られるもっともシンプルな図形は、四面体OABCである。
で作られるもっともシンプルな図形は、四面体OABCである。
空間内の任意の点、たとえば点P,Qは次のように表される。
 =u1
=u1 +v1
+v1 +w1
+w1
 =u2
=u2 +v2
+v2 +w2
+w2
これらの内積は、
 ・
・ =u1u2
=u1u2 ・
・ +v1v2
+v1v2 ・
・ +w1w2
+w1w2 ・
・
+(u1v2+u2v1) ・
・ +(v1w2+v2w1)
+(v1w2+v2w1) ・
・ +(w1u2+w2u1)
+(w1u2+w2u1) ・
・
したがって、2個のベクトルの内積の計算過程には、 ・
・ ,
, ・
・ ,
, ・
・ ,
, ・
・ ,
, ・
・ ,
, ・
・ という、6種類の項しか出てこないことがわかる。
という、6種類の項しか出てこないことがわかる。
これは、四面体が「確定」するためには、その側面を構成する3個の三角形が「合同条件」を満たしていること、すなわち、
「辺OAの長さ」、「辺OBの長さ」、「辺OCの長さ」、∠AOB、∠BOC、∠COAの6個の要素が「わかって」いればよい、ということを意味している。空間内の3個の1次独立なベクトルを、  ,
, ,
, とすると、
とすると、
- これらの1次結合で、空間内のすべてのベクトルを表現でき、
- これらの3個のベクトルから作られる「6種類の内積の値」、
 ・
・ ,
, ・
・ ,
, ・
・ ,
, ・
・ ,
, ・
・ ,
, ・
・ がわかっていれば、その空間内のどのような点であったとしても、それらを結んでできる「線分の長さ」や、「線分同士のなす角」をすべて、計算することができる。
がわかっていれば、その空間内のどのような点であったとしても、それらを結んでできる「線分の長さ」や、「線分同士のなす角」をすべて、計算することができる。
ここまでの話で、次のことが明らかになった。
- 平面上のすべての点は、2個の1次独立ベクトルの1次結合で表現する方法があること。
空間内のすべての点は、3個の1次独立ベクトルの1次結合で表現する方法があること。 - 辺の長さやそれらのなす角が定まった、特定の三角形を問題にするときは、3個の内積の値がわかっている必要があること。
辺の長さやそれらのなす角が定まった、特定の四面体を問題にするときは、6個の内積の値がわかっている必要があること。
- [カテゴリー1]「内積」を用いない平面ベクトルの問題
ここでは、辺の長さやそれらのなす角など、具体的な「大きさ」、「角度」を特定しない、任意の、あらゆる形の三角形に共通する問題を扱う。
与えられる数値はすべて絶対的な「大きさ」、「角度」に関するものではなく、相対的な「長さの比」のみである。
頂点と辺の内分点・外分点を結ぶ線分同士の「交点を求める」ことが主眼となる。 - [カテゴリー2]「内積」を用いない空間ベクトルの問題
ここでは、辺の長さやそれらのなす角など、具体的な「大きさ」、「角度」を特定しない、任意の、あらゆる形の四面体に共通する問題を扱う。
与えられる数値はすべて絶対的な「大きさ」、「角度」に関するものではなく、相対的な「長さの比」のみである。
頂点と辺の内分点・外分点を結ぶ線分と、これらの中から選んだ3点が構成する平面との「交点を求める」こと、が主眼となる。 - [カテゴリー3]「内積」を用いる平面ベクトルの問題
2個の1次独立ベクトルと、それらを組み合わせてできる3種類の内積の値が既知である場合、辺の長さ、それらのなす角が具体的に定まった、特定の三角形について問題にすることができる。
特定の点を結んでできる線分の長さ、線分同士のなす角、特に、「垂線の足」の位置、垂線の長さなど。 - [カテゴリー4]「内積」を用いる空間ベクトルの問題
3個の1次独立ベクトルと、それらを組み合わせてできる6種類の内積の値が既知である場合、辺の長さ、それらのなす角が具体的に定まった、特定の四面体について問題にすることができる。
特定の点を結んでできる線分の長さ、線分同士のなす角、線分と平面のなす角、特に、「点から平面に降ろした垂線の足」の位置、垂線の長さなど。
| 平面 | 空間 | |
| 内積を用いない |
[カテゴリー1]
任意の形の三角形に共通の問題
|
[カテゴリー2]
任意の形の四面体に共通の問題
|
| 内積を用いる |
[カテゴリー3]
特定の形の三角形に関する問題
|
[カテゴリー4]
特定の形の四面体に関する問題
|
-
これらの問題の解決に必要な「ツール」は、以下のとおりである。
- 始点のつけかえルール
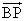 =
= -
-
始点Bから見た点Pを表す位置ベクトル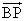 を、新たな始点Aから表現したければ、元の終点を表す位置ベクトル
を、新たな始点Aから表現したければ、元の終点を表す位置ベクトル から、元の始点を表す位置ベクトル
から、元の始点を表す位置ベクトル を引けばよい。
を引けばよい。
- 3点が同一直線上にある条件(共線条件)
異なる2点ABを特定すれば、これを結ぶ直線ABは、ただ一つ定まる。
ここに第3の点Pを持ち込むとき、Pが直線AB上に存在するには、どのような条件を満たすことが必要であろうか?
ベクトルは、「大きさ」と「方向」のみを要素とする。A,P,Bが同一直線上に並んでいるのなら、ベクトル とベクトル
とベクトル は「重なって」いる。
は「重なって」いる。
「重なって」いるとは、「方向」は同じだが、「大きさ」については、同じかもしれないし、同じでないかもしれない、つまり「わからない」ことを意味する。
2個のベクトルが「等しい」、すなわち「大きさ」も「方向」も同じとき、それらは等号で結んでよい。「方向」は同じだが、「大きさ」が異なるのならば、一方が他方の「定数倍」に等しいと書くことができる。すなわち、
 =t
=t
この式が、3点A,P,Bが同一直線上にある条件を、完全に記述している。
これを、上の「始点のつけかえルール」により、任意の始点から「見た」表現形式に変えることができる。たとえば、始点をOとすると、
 -
- =t(
=t( -
- )
)
 を右辺に移項して同類項をまとめると、
を右辺に移項して同類項をまとめると、
 =(1-t)
=(1-t) +t
+t
また、もう一つ別の表現をするならば、
 =p
=p +q
+q ただし、p+q=1
ただし、p+q=1
- 4点が同一平面上にある条件(共面条件)
互いに異なり、かつ同一直線上にない3点ABCを特定すれば、これらを含む平面は、ただ一つ定まる。
ここに第4の点Pを持ち込むとき、PがABCを含む平面上に存在するには、どのような条件を満たすことが必要であろうか?
「平面上の任意の点を表す位置ベクトルは、その平面上に存在する2個の1次独立なベクトルの1次結合で、ただ一通りに表現できる」。
ここで、ベクトル とベクトル
とベクトル は、3点ABCが同一直線上にない以上、互いに1次独立である。
は、3点ABCが同一直線上にない以上、互いに1次独立である。
点Pが、ABCを含む平面上に存在するのなら、ベクトル は、これら2個に1次独立ベクトルの1次結合「だけ」で表現されなければならない。すなわち、
は、これら2個に1次独立ベクトルの1次結合「だけ」で表現されなければならない。すなわち、
 =u
=u +v
+v
この式が、4点A,B,C,Pが同一平面上にある条件を、完全に記述している。
これを、上の「始点のつけかえルール」により、任意の始点から「見た」表現形式に変えることができる。たとえば、始点をOとすると、
 -
- =u(
=u( -
- )+v(
)+v( -
- )
)
 を右辺に移項して同類項をまとめると、
を右辺に移項して同類項をまとめると、
 =(1-u-v)
=(1-u-v) +u
+u +v
+v
また、もう一つ別の表現をするならば、
 =p
=p +q
+q +r
+r ただし、p+q+r=1
ただし、p+q+r=1
- 内積の定義
 ・
・
 =|
=| ||
|| |cosθ
|cosθ
ただし、θ=∠AOB
- [カテゴリー4]にのみ特有のツールとして、
「直線と平面が垂直である」ことの定義。- 第1の定義
直線lと平面αが垂直であるとは、αに含まれれる任意の直線と、直線lとが垂直であることである。
ところで、平面α上の任意の点を表す位置ベクトルは、αを構成する2個の1次独立なベクトルの1次結合で表現できるから、これらの点を結ぶ直線もまた、αを構成する2個の1次独立ベクトルの1次結合で「かならず」表現できるはずである。
したがって、 - 第2の定義
直線lと平面αが垂直であるとは、αを構成する2個の1次独立ベクトルと、直線lとが垂直であることである。
- 第1の定義
-
以上の事柄を踏まえて、「問題の処理手順」をマニュアル化しよう。
平面 空間 内積を用いない [カテゴリー1] - 始点を決める
- 2個の1次独立ベクトルを選ぶ
- 他の点(1次従属な点)の位置ベクトルを、これら2個の1次独立ベクトルの1次結合で表現する
- 始点のつけかえルール
- 共線条件
[カテゴリー2] - 始点を決める
- 3個の1次独立ベクトルを選ぶ
- 他の点(1次従属な点)の位置ベクトルを、これら3個の1次独立ベクトルの1次結合で表現する
- 始点のつけかえルール
- 共線条件
- 共面条件
内積を用いる [カテゴリー3] - 始点を決める
- 2個の1次独立ベクトルを選ぶ
- 他の点(1次従属な点)の位置ベクトルを、これら2個の1次独立ベクトルの1次結合で表現する
- これら2個の1次独立ベクトルを組み合わせてできる3種類の内積の値を求める
- 始点のつけかえルール
- 共線条件
- 内積の定義
[カテゴリー4] - 始点を決める
- 3個の1次独立ベクトルを選ぶ
- 他の点(1次従属な点)の位置ベクトルを、これら3個の1次独立ベクトルの1次結合で表現する
- これら3個の1次独立ベクトルを組み合わせてできる6種類の内積の値を求める
- 始点のつけかえルール
- 共線条件
- 共面条件
- 内積の定義
- 直線と平面が垂直であることの定義
- [例題1]△ABCの辺BCを1:2に内分する点をD、辺CAを3:2に内分する点をE、線分ADと線分BEの交点をFとするとき、Fを表す位置ベクトル
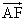 を、
を、 ,
, を用いて表せ。また、AF:FD,BF:FEの値を求めよ。
を用いて表せ。また、AF:FD,BF:FEの値を求めよ。
- [例題2]△ABCの重心Gを表す位置ベクトル
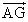 を、
を、 ,
, を用いて表せ。
を用いて表せ。
- [例題3]四面体ABCDにおいて、辺ABを2:1に内分する点をL、辺BCの中点をM、辺CDを2:1に内分する点をN、△ACDの重心をGとする。3点L,M,Nを含む平面と線分BGの交点をPとするとき、BP:PGを求めよ。
- [例題4]四面体OABCにおいて、△OAB,△OBC,△OCA,△ABCの重心をそれぞれD,E,F,Gとする。線分DC,EA,FB,GOは1点で交わることを証明せよ。
- [例題5]四面体ABCDにおいて、ABを1:2に内分する点をL、ACを2:3に内分する点をM、ADを5:2に内分する点をN、CDの中点をS、直線BMと直線CLの交点をP、直線CNと直線ASの交点をQとするとき、DPとBQは交わらないことを証明せよ。
- [例題6]△ABCにおいて、AB=AC=2,BC=1とする。次のものを求めよ。
- Bから辺ACに下ろした垂線の足をHとするとき、AHの長さ。
- ACの垂直2等分線とABの交点をPとするとき、APの長さ。
- ∠Bの2等分線とACの交点をQとするとき、AQの長さ。
- △ABCの面積。
- [例題7]△ABCにおいて、
- ∠ABC,∠BCA,∠CABの2等分線は、1点で交わることを示せ。[内心]
- 辺AB,BC,CAの垂直2等分線は、1点で交わることを示せ。[外心]
- 頂点C,A,Bから、それぞれ辺AB,BC,CAに下ろした垂線は、1点で交わることを示せ。[垂心]
- 外心をO、垂心をHとするとき、以下の式が成り立つことを示せ。
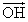 =
= +
+ +
+
さらに、重心をGとするとき、3点G,O,Hは同一直線上にあることを示し、OG:GHを求めよ。
- [例題8]
4点O(0,0,0),A(1,0,0),B(0,1,0),C(0,0,
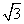 )を頂点とする四面体OABCについて、Oから△ABCを含む平面に下ろした垂線の足をHとするとき、OHの長さ、および、cos∠OAHの値を求めよ。
)を頂点とする四面体OABCについて、Oから△ABCを含む平面に下ろした垂線の足をHとするとき、OHの長さ、および、cos∠OAHの値を求めよ。
- [例題9]
- 四面体OABCにおいて、△OAB,△OBC,△OCA,△ABCの重心をそれぞれD,E,F,Gとする。線分DC,EA,FB,GOは1点で交わることを証明せよ。
- 四面体OABCは1辺の長さ1の正四面体であるとする。上で求めた、線分DC,EA,FB,GOの交点をP、∠OPA=θとするとき、cosθの値を求めよ。
- [例題1]△ABCの辺BCを1:2に内分する点をD、辺CAを3:2に内分する点をE、線分ADと線分BEの交点をFとするとき、Fを表す位置ベクトル
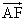 を、
を、 ,
, を用いて表せ。また、AF:FD,BF:FEの値を求めよ。
を用いて表せ。また、AF:FD,BF:FEの値を求めよ。
[処理手順]- 始点はAにする。
- 1次独立な2個のベクトルとして、
 ,
, を選ぶ。
を選ぶ。
- 他の点(1次従属な点)はD,E,Fであるから、これらの点の始点をAとした位置ベクトル、
 ,
,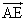 ,
,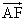 を、上の2個のベクトルの1次結合として表現することが目標である。
を、上の2個のベクトルの1次結合として表現することが目標である。
-
DはBCを1:2に内分する点である。
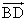 =
=

始点をAに変える。
 -
- =
= (
( -
- )
)
 =
=
 +
+
 ・・・①
・・・①
これを一般化して、「内分点・外分点」を表す位置ベクトルを求めておく。
こうして、「内分点」を表す位置ベクトル 「外分点」を表す位置ベクトル 「PがABをm:nに内分する」とは、
点A,Bからそれぞれ「内側に向かって」点Pを「眺めた」とき、AP:PBの比がm:nであることを意味する。
AP:AB=AP:(AP+PB)=m:(m+n)
であるから、
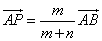
始点をAに変える。
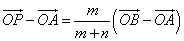
移項してまとめると、
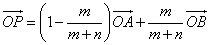
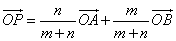
「PがABをm:nに外分する」とは、
点A,Bのいずれかから「外側に向かって」点Pを「眺めた」とき、AP:PBの比がm:nであることを意味する。
点A,Bのどちらの外側になるかは、m,nの大小関係による。-
m>nのとき、PはBの「外側」にある。つまり、3点はA,B,Pの順に並んでいる。
AP:AB=AP:(AP-PB)=m:(m-n) -
m<nのとき、PはAの「外側」にある。つまり、3点はP,A,Bの順に並んでいる。
PA:AB=PA:(PB-PA)=m:(m-n)
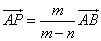
始点をAに変える。
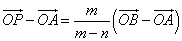
移項してまとめると、
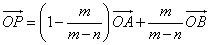
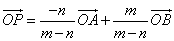
ABをm:nに内分する点Pを表す位置ベクトルは、
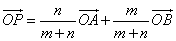
PがABをm:nに外分するときは、nを-nと「読みかえ」て、
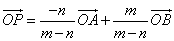
-
m>nのとき、PはBの「外側」にある。つまり、3点はA,B,Pの順に並んでいる。
-
EはCAを3:2に内分する点(ACを2:3に内分する点)である。
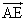 =
=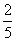
 ・・・②
・・・②
-
FはADとBEの交点である。[直線と直線の交点の求め方]
-
FはAD上の点であるから、
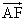 =s
=s
と書ける。ただし、AF:FD=s:(1-s)
①より、
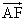 =
= s
s +
+ s
s ・・・③
・・・③
-
FはBE上の点であるから、
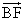 =t
=t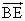
と書ける。ただし、BF:FE=t:(1-t)
始点をAに変えて、
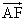 =(1-t)
=(1-t) +t
+t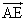
②より、
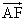 =(1-t)
=(1-t) +
+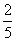 t
t ・・・④
・・・④
③④より、 ,
, はいずれも零ベクトルではなく、互いに平行でないから(1次独立)、それぞれの係数は等しく、
はいずれも零ベクトルではなく、互いに平行でないから(1次独立)、それぞれの係数は等しく、
 s=1-t
s=1-t
 s=
s=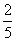 t
t
といえる。この、s,tに関する連立方程式を解いて、
s=
t=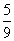
したがって、
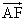 =
=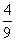
 +
+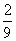

また、
AF:FD=s:(1-s)= :
: =2:1
=2:1
BF:FE=t:(1-t)=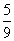 :
: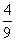 =5:4
=5:4
直線と直線の交点の求め方 求める点が、
一方の直線上にあることから、未知数が1個
他方の直線上にもあることから、未知数が1個
2次元平面では、1次独立なベクトルの個数は2個だから、その係数に関する条件式は2個
一般に、未知数の個数と、独立な条件式の個数が一致しているとき、その連立方程式は、解を持つ
だから、交点としてただ一つの解が求められる。 -
FはAD上の点であるから、
- [例題2]△ABCの重心Gを表す位置ベクトル
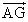 を、
を、 ,
, を用いて表せ。
を用いて表せ。
辺ABの中点をL、辺ACの中点をM、辺BCの中点をNとする。三角形の「重心」 三角形の各頂点とその対辺の中点を結ぶ線分を「中線」と呼ぶ。
どのような三角形でも、3本の中線は一点で交わる。これを三角形の「重心」と呼ぶ。
均一な材質でできた三角形の板の「重心」に糸をつけて吊り下げると、3頂点を地表面に平行な同一平面上に保ったまま安定する。
「重力」の作用する中心であることから「重心」と名づけられた。
ここで解決すべき事柄は、- 線分CLと線分BMとの交点G1を求める、すなわち
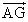 1を、1次独立な2個のベクトル
1を、1次独立な2個のベクトル ,
, の1次結合で表すこと。
の1次結合で表すこと。
- G1が線分AN上にあること、すなわち、A,G1,Nが同一直線上にあることを示すこと。
[処理手順]- 始点はAにする。
- 1次独立な2個のベクトルとして、
 ,
, を選ぶ。
を選ぶ。
- 他の点(1次従属な点)はL,M,N,G1であるから、これらの点の始点をAとした位置ベクトル、
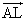 ,
,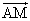 ,
,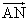 ,
,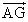 1を、上の2個のベクトルの1次結合として表現することが目標である。
1を、上の2個のベクトルの1次結合として表現することが目標である。
- Lは線分ABの中点である。
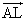 =
=
 ・・・①
・・・①
- Mは線分ACの中点である。
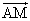 =
=
 ・・・②
・・・②
- Nは線分BCの中点である。
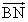 =
=

始点をAに変えると、
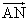 =
=
 +
+
 ・・・③
・・・③
- G1は線分CLと線分BMとの交点である。
- G1は線分CL上にある。
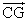 1=s
1=s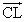
始点をAに変えると、
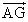 1=(1-s)
1=(1-s)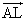 +s
+s
①より、
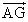 1=
1= (1-s)
(1-s) +s
+s ・・・④
・・・④
- G1は線分BM上にある。
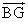 1=t
1=t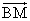
始点をAに変えると、
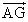 1=(1-t)
1=(1-t)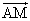 +t
+t
②より、
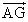 1=t
1=t +
+ (1-t)
(1-t) ・・・⑤
・・・⑤
 ,
, は、いずれも零ベクトルでなく、互いに平行でないから、
は、いずれも零ベクトルでなく、互いに平行でないから、
 (1-s)=t
(1-s)=t
s= (1-t)
(1-t)
これらを満たすs,tは、
s=t=
よって、
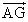 1=
1=
 +
+
 ・・・⑥
・・・⑥
ところで、③より、
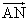 =
=
 +
+
 ・・・③
・・・③
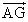 1=
1= (
(
 +
+
 )=
)=
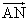
こうして、A,G1,Nが同一直線上にあることが示された。
ここで、あらためてG1をGとして、定義しなおすと、
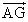 =
=
 +
+

三角形の重心 △ABCの重心Gを表す位置ベクトル
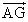 =
=
 +
+

これを始点Oとして書き直すと、
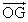 -
- =
= (
( -
- )+
)+ (
( -
- )
)
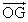 =
=
 +
+
 +
+

- G1は線分CL上にある。
- 線分CLと線分BMとの交点G1を求める、すなわち
- [例題3]四面体ABCDにおいて、辺ABを2:1に内分する点をL、辺BCの中点をM、辺CDを2:1に内分する点をN、△ACDの重心をGとする。3点L,M,Nを含む平面と線分BGの交点をPとするとき、BP:PGを求めよ。
[処理手順]- 始点はAにする。
- 1次独立な3個のベクトルとして、
 ,
, ,
, を選ぶ。
を選ぶ。
- 他の点(1次従属な点)はL,M,N,Gであるから、これらの点の始点をAとした位置ベクトル、
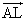 ,
,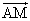 ,
,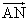 ,
,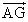 を、上の3個のベクトルの1次結合として表現することが目標である。
を、上の3個のベクトルの1次結合として表現することが目標である。
- LはABを2:1に内分する点であるから、
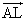 =
=
 ・・・①
・・・①
- MはBCの中点、すなわちBCを1:1に内分する点であるから、
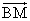 =
=

始点をAに変える。
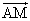 =
=
 +
+
 ・・・②
・・・②
- NはCDを2:1に内分する点であるから、
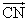 =
=
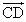
始点をAに変える。
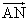 =
=
 +
+
 ・・・③
・・・③
- Gは△ACDの重心であるから、[例題2]の結果より、
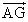 =
=
 +
+
 ・・・④
・・・④
- PはL,M,Nを含む平面と線分BGの交点である。[平面と直線の交点の求め方]
- PはL,M,Nを含む平面上にあるから、
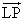 =u
=u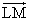 +u
+u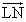
始点をAに変える。
 -
-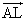 =u(
=u(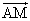 -
-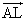 )+v(
)+v(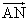 -
-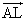 )
)
 =(1-u-v)
=(1-u-v)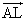 +u
+u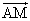 +v
+v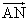
①②③より、
 =
= (1-u-v)
(1-u-v) +u(
+u(
 +
+
 )+v(
)+v(
 +
+
 )
)
 =(
=( -
-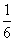 u-
u- v)
v) +(
+( u+
u+ v)
v) +
+ v
v ・・・⑤
・・・⑤
- PはBG上にあるから、
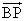 =w
=w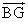
始点をAに変える。
 -
- =w(
=w(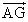 -
- )
)
 =(1-w)
=(1-w) +w
+w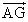
④より、
 =(1-w)
=(1-w) +w(
+w(
 +
+
 )
)
 =(1-w)
=(1-w) +
+ w
w +
+ w
w ・・・⑥
・・・⑥
 ,
, ,
, はいずれも零ベクトルではなく、どの2個も互いに平行でなく、かつ同一平面上にないから(1次独立)、それぞれの係数は等しく、
はいずれも零ベクトルではなく、どの2個も互いに平行でなく、かつ同一平面上にないから(1次独立)、それぞれの係数は等しく、
 -
-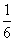 u-
u- v=1-w
v=1-w
 u+
u+ v=
v= w
w
 v=
v= w
w
この、u,v,wに関する連立方程式を解いて、
u=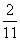 ,v=
,v=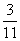 ,w=
,w=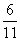
 =
=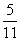
 +
+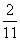
 +
+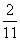

したがって、BP:PG=w:(1-w)=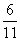 :
: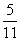 =6:5
=6:5
平面と直線の交点の求め方 求める点が、
ある平面上にあることから、未知数が2個
またある直線上にもあることから、未知数が1個
3次元空間では、1次独立なベクトルの個数は3個だから、その係数に関する条件式は3個
一般に、未知数の個数と、独立な条件式の個数が一致しているとき、その連立方程式は、解を持つ
だから、交点としてただ一つの解が求められる。「自由度」について - 1次元数直線上の1点を特定しようとすれば、ただ一つの数値を指定すればよい。
自由に選ぶことのできる数値が一つであるから、これを「自由度」1と呼ぶ。 - 2次元平面上の1点を特定しようとすれば、二つの数値を組を指定すればよい。
自由に選ぶことのできる数値が二つであるから、これを「自由度」2と呼ぶ。 - 3次元空間内の1点を特定しようとすれば、三つの数値を組を指定すればよい。
自由に選ぶことのできる数値が三つであるから、これを「自由度」3と呼ぶ。
1次独立なベクトルの個数と、「自由度」が、対応していることがわかる。
- PはL,M,Nを含む平面上にあるから、
同じ問題を、始点をBとして解くこともできる。
[処理手順]- 始点はBにする。
- 1次独立な3個のベクトルとして、
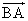 ,
, ,
,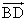 を選ぶ。
を選ぶ。
- 他の点(1次従属な点)はL,M,N,Gであるから、これらの点の始点をBとした位置ベクトル、
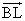 ,
,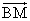 ,
,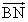 ,
,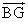 を、上の3個のベクトルの1次結合として表現することが目標である。
を、上の3個のベクトルの1次結合として表現することが目標である。
- LはABを2:1に内分する点(BAを1:2に内分する点)であるから、
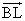 =
=
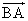 ・・・①
・・・①
- MはBCの中点、すなわちBCを1:1に内分する点であるから、
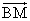 =
=
 ・・・②
・・・②
- NはCDを2:1に内分する点であるから、
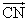 =
=
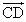
始点をBに変える。
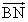 =
=
 +
+
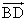 ・・・③
・・・③
- Gは△ACDの重心であるから、[例題2]の結果より、
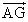 =
=
 +
+

始点をBに変える。
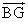 =
=
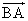 +
+
 +
+
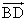 ・・・④
・・・④
- PはL,M,Nを含む平面と線分BGの交点である。[平面と直線の交点の求め方]
- PはL,M,Nを含む平面上にあるから、
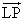 =u
=u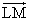 +u
+u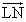
始点をBに変える。
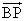 -
-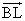 =u(
=u(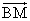 -
-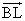 )+v(
)+v(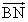 -
-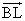 )
)
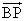 =(1-u-v)
=(1-u-v)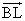 +u
+u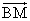 +v
+v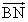
①②③より、
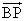 =
= (1-u-v)
(1-u-v)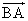 +
+ u
u +v(
+v(
 +
+
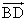 )
)
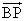 =
= (1-u-v)
(1-u-v)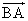 +(
+( u+
u+ v)
v) +
+ v
v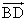 ・・・⑤
・・・⑤
- PはBG上にあるから、
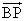 =w
=w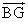
④より、
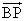 =
= w
w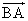 +
+ w
w +
+ w
w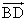 ・・・⑥
・・・⑥
 ,
, ,
, はいずれも零ベクトルではなく、どの2個も互いに平行でなく、かつ同一平面上にないから(1次独立)、それぞれの係数は等しく、
はいずれも零ベクトルではなく、どの2個も互いに平行でなく、かつ同一平面上にないから(1次独立)、それぞれの係数は等しく、
 (1-u-v)=
(1-u-v)= w
w
 u+
u+ v=
v= w
w
 v=
v= w
w
この、u,v,wに関する連立方程式を解いて、
u=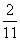 ,v=
,v=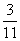 ,w=
,w=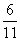
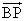 =
=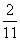
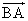 +
+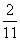
 +
+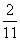
したがって、BP:PG=w:(1-w)=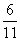 :
: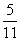 =6:5
=6:5
このように、問題の解決方法は、始点の選び方、1次独立なベクトルのセットの選び方に依存しない。 - PはL,M,Nを含む平面上にあるから、
- [例題4]四面体OABCにおいて、△OAB,△OBC,△OCA,△ABCの重心をそれぞれD,E,F,Gとする。線分DC,EA,FB,GOは1点で交わることを証明せよ。
[処理手順]- 始点はOにする。
- 1次独立な3個のベクトルとして、
 ,
, ,
, を選ぶ。
を選ぶ。
- 他の点(1次従属な点)はD,E,F,Gであるから、これらの点の始点をOとした位置ベクトル、
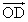 ,
, ,
,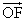 ,
,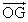 を、上の3個のベクトルの1次結合として表現する。
を、上の3個のベクトルの1次結合として表現する。
- CDとAEの交点をPとする。[空間直線の交点]
- PがBF上にあることを証明する。
- 同様に、PがOG上にもあることを証明する。
[空間直線の交点]にまつわる問題点 - 2次元平面では、「平行でない2直線は必ず交わる」。
これは、平行でない2直線の交点を求める「連立方程式」が「解を持つ」ことに対応する。
求める点が、一方の直線上にあることから1個の未知数が、またもう一方の直線上にもあることからもう1個、合計2個の未知数が導入される。
2次元平面の「1次独立」なベクトルの個数は2であるから、これら2個の未知数の関係を表す「条件式」の個数は2である。
だから、ただ一つの解が定まる。 - 3次元空間では、「平面と、これと平行でない直線は必ず交わる」。
これは、平面と、これと平行でない直線の交点を求める「連立方程式」が「解を持つ」ことに対応する。
求める点が、一方の平面上にあることから2個の未知数が、またもう一方の直線上にもあることからもう1個、合計3個の未知数が導入される。
3次元空間の「1次独立」なベクトルの個数は3であるから、これら3個の未知数の関係を表す「条件式」の個数は3である。
だから、ただ一つの解が定まる。 - 3次元空間では、「平行でない2直線は、必ず交わるとは言えない」。
互いに平行な2平面上に存在する直線同士のうち、互いに平行でない直線同士の関係を「ねじれの位置」と呼ぶ。
これは、2個の空間直線の交点を求める「連立方程式」が「解を持たない可能性がある」ことに対応する。
求める点が、一方の直線上にあることから1個の未知数が、またもう一方の直線上にもあることからもう1個、合計2個の未知数が導入される。
3次元空間の「1次独立」なベクトルの個数は3であるから、これら3個の未知数の関係を表す「条件式」の個数は3である。
未知数の個数より、条件式の個数のほうが多いから、このような条件を見たす解のセットが「存在しない」可能性が生じる。
- 2次元平面では、「平行でない2直線は必ず交わる」。
-
Dは△OABの重心だから、
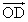 =
=
 +
+


-
Eは△OBCの重心だから、
 =
=
 +
+


-
Fは△OCAの重心だから、
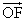 =
=
 +
+


-
Gは△ABCの重心だから、
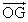 =
=
 +
+
 +
+


- CDとAEの交点を求めたい。しかし、「交わるかどうか」がわからないので、次のように処理する。
CD上の点P1と、AE上の点P2とをそれぞれ別個に表現し、これらが「一致する」可能性があることを証明する。
P1はCD上の点だから、
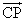 1=s
1=s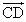
 1-
1- =s(
=s(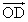 -
- )
)
 1=(1-s)
1=(1-s) +s
+s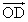
 1=
1= s
s +
+ s
s +(1-s)
+(1-s) ・・・①
・・・①
P2はAE上の点だから、
 2=s
2=s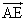
 2-
2- =t(
=t( -
- )
)
 2=(1-t)
2=(1-t) +t
+t
 2=(1-t)
2=(1-t) +
+ t
t +
+ t
t ・・・②
・・・②
①②より、2点P1,P2が一致するとすれば、 ,
, ,
, は、いずれも
は、いずれも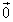 でなく、どの2個も互いに平行でなく、かつ同一平面上にない(1次独立)ことから、以下の3式を同時に満たすs,tが存在するはずである。[2個の未知数と3個の条件式]
でなく、どの2個も互いに平行でなく、かつ同一平面上にない(1次独立)ことから、以下の3式を同時に満たすs,tが存在するはずである。[2個の未知数と3個の条件式]
・ s=1-t
s=1-t
・ s=
s= t
t
・1-s= t
t
s=t=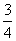 はこれらを同時に満たすから、P1,P2は一致する。これを新たに点Pとすれば、
はこれらを同時に満たすから、P1,P2は一致する。これを新たに点Pとすれば、
 =
=
 +
+
 +
+

- 始点をBに変えると、
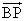 -
-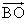 =
= (
(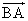 -
- )-
)-
 +
+ (
( -
- )
)
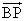 =
=
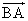 +
+
 +
+
 ・・・③
・・・③
また、
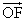 =
=
 +
+


だから、これもBを始点として書き直すと、
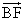 -
- =
= (
(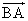 -
- )+
)+ (
( -
- )
)
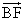 =
=
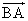 +
+
 +
+
 ・・・④
・・・④
③④から、
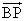 =
=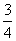
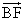
となり、こうして点Pが直線BF上にあることが示された。 -
また、
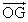 =
=
 +
+
 +
+


であるから、
 =
=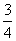
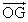
となり、こうして点Pが直線OG上にあることが示された。 -
以上から、線分DC,EA,FB,GOは1点で交わり、その交点Pは次のように表されることがわかった。
 =
=
 +
+
 +
+

(この点Pは、四面体OABCの「重心」をあらわすことが知られている。)
重心 線分OA 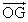 =
=

△OAB 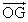 =
=
 +
+

四面体OABC 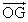 =
=
 +
+
 +
+

- [例題5]四面体ABCDにおいて、ABを1:2に内分する点をL、ACを2:3に内分する点をM、ADを5:2に内分する点をN、CDの中点をS、直線BMと直線CLの交点をP、直線CNと直線ASの交点をQとするとき、DPとBQは交わらないことを証明せよ。
[処理手順]- 始点はAにする。
- 1次独立な3個のベクトルとして、
 ,
, ,
, を選ぶ。
を選ぶ。
- 他の点(1次従属な点)はL,M,N,S,P,Qであるから、これらの点の始点をAとした位置ベクトル、
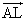 ,
,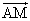 ,
,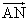 ,
,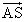 ,
, ,
,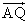 を、上の3個のベクトルの1次結合として表現する。
を、上の3個のベクトルの1次結合として表現する。
- DP上の点をR1、BQ上の点をR2としたとき、R1,R2が決して同一の点とはなり得ないこと、すなわち、
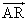 1と
1と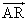 2が、1次独立な3個のベクトル
2が、1次独立な3個のベクトル ,
, ,
, の1次結合として、同一の式では表現できないことを示す。
[空間直線の交点]
の1次結合として、同一の式では表現できないことを示す。
[空間直線の交点]
- LはABを1:2に内分する点
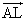 =
=

- MはACを2:3に内分する点
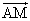 =
=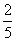

- NはADを5:2に内分する点
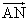 =
=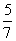

- SはCDの中点
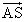 =
=
 +
+

- Pは直線BMと直線CLの交点
- PはBM上
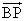 =s
=s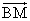
 -
- =s(
=s(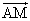 -
- )
)
 =(1-s)
=(1-s) +s
+s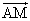
 =(1-s)
=(1-s) +
+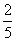 s
s ・・・①
・・・①
- PはCL上
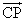 =t
=t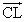
 -
- =t(
=t(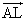 -
- )
)
 =(1-t)
=(1-t) +t
+t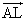
 =
= t
t +(1-t)
+(1-t) ・・・②
・・・②
- ①②より、
 ,
, は、いずれも
は、いずれも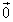 でなく、互いに平行でないから(1次独立)、
でなく、互いに平行でないから(1次独立)、
・1-s= t
t
・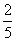 s=1-t
s=1-t
s=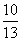 ,t=
,t=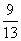
したがって、
 =
=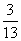
 +
+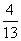

- PはBM上
- Qは直線CNと直線ASの交点
- QはCN上
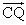 =u
=u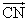
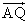 -
- =u(
=u(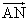 -
- )
)
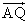 =(1-u)
=(1-u) +u
+u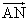
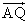 =(1-u)
=(1-u) +
+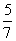 u
u ・・・③
・・・③
- QはAS上
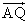 =v
=v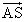
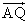 =
= v
v +
+ v
v ・・・④
・・・④
- ③④より、
 ,
, は、いずれも
は、いずれも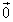 でなく、互いに平行でないから(1次独立)、
でなく、互いに平行でないから(1次独立)、
・1-u= v
v
・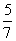 u=
u= v
v
u=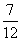 ,t=
,t=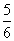
したがって、
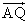 =
=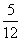
 +
+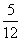

- QはCN上
-
DP上に点R1、BQ上に点R2をとる。
-
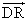 1=x
1=x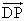
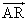 1=(1-x)
1=(1-x) +x
+x
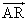 1=(1-x)
1=(1-x) +x(
+x(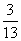
 +
+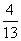
 )
)
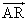 1=
1=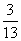 x
x +
+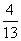 x
x +(1-x)
+(1-x) ・・・⑤
・・・⑤
-
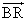 2=y
2=y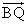
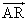 2=(1-y)
2=(1-y) +y
+y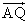
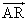 2=(1-y)
2=(1-y) +y(
+y(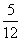
 +
+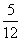
 )
)
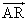 2=(1-y)
2=(1-y) +
+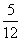 y
y +
+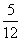 y
y ・・・⑥
・・・⑥
-
⑤⑥より、
 ,
, ,
, は、いずれも
は、いずれも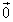 でなく、どの2個も互いに平行でなく、かつ同一平面上にないから(1次独立)、
でなく、どの2個も互いに平行でなく、かつ同一平面上にないから(1次独立)、
R1,R2が一致するとすれば、以下の3式を同時に満たすx,yが存在するはずである。[2個の未知数と3個の条件式]
・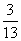 x=1-y
x=1-y
・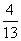 x=
x=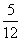 y
y
・1-x=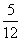 y
y
しかし、これらの3式を同時に満たすx,yは存在しないから、点R1と点R2は一致することがない。すなわち、
直線DPと直線BQは共有点を持たない。
-
- [例題6]△ABCにおいて、AB=AC=2,BC=1とする。次のものを求めよ。
- Bから辺ACに下ろした垂線の足をHとするとき、AHの長さ。
- ACの垂直2等分線とABの交点をPとするとき、APの長さ。
- ∠Bの2等分線とACの交点をQとするとき、AQの長さ。
- △ABCの面積。
- 始点はAにする。
- 1次独立な2個のベクトルとして、
 ,
, を選ぶ。
を選ぶ。
- 他の点(1次従属な点)はH,P,Qであるから、これらの点の始点をAとした位置ベクトル、
 ,
, ,
,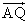 を、上の2個のベクトルの1次結合として表現することが目標である。
を、上の2個のベクトルの1次結合として表現することが目標である。
- ここでは、「垂線」、「垂直」、「角の2等分線」、「長さ」など、「角度」および、絶対的な「長さ」が問題となっているから、「内積」を用いる必要が生じる。
三角形が「確定」するには3個の内積の値、 ・
・ ,
, ・
・ ,
, ・
・ がわかっていることが必要である。
がわかっていることが必要である。
 ・
・ =|
=| |2=22=4
|2=22=4
 ・
・ =|
=| |2=22=4
|2=22=4
 ・
・ は、BC=1であることから、次のようにして求めることができる。
は、BC=1であることから、次のようにして求めることができる。
 ・
・ =|
=| |2=12=1
|2=12=1
( -
- )・(
)・( -
- )=1
)=1
 ・
・ -2
-2 ・
・ +
+ ・
・ =1
=1
4-2 ・
・ +4=1
+4=1
 ・
・ =
=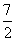
- Bから辺ACに下ろした垂線の足をHとするとき、AHの長さ。
Hは、「Bから辺ACに下ろした垂線の足」、これを次の2つの「事実」に分解して考える。- Hは直線AC上にある。
 =t
=t ・・・①
・・・①
- BH⊥ACである。
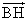 ・
・ =0・・・②
=0・・・②
( -
- )・
)・ =0
=0
①を代入する。
(t -
- )・
)・ =0
=0
( -t
-t )・
)・ =0
=0
 ・
・ -t
-t ・
・ =0
=0
上で得られた「内積」の値を代入する。
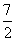 -4t=0
-4t=0
t=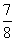
 =
=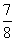

こうして、Hの場所がわかった。AHの長さは、
| |=
|=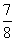 |
| |=
|=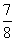 ×2=
×2=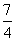
- Hは直線AC上にある。
- ACの垂直2等分線とABの交点をPとするとき、APの長さ。
- PはAB上にある。
 =t
=t ・・・①
・・・①
- PはACの垂直2等分線上にある。
ACの中点をMとすると、
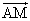 =
=
 ・・・②
・・・②
PM⊥AC
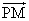 ・
・ =0
=0
始点をAに変えて、
(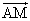 -
- )・
)・ =0
=0
(
 -t
-t )・
)・ =0
=0
(t -
-
 )・
)・ =0
=0
t ・
・ -
-
 ・
・ =0
=0
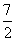 t-
t- ×4=0
×4=0
t=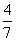
 =
=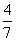

こうして、Pの場所がわかった。APの長さは、
| |=
|=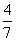 |
| |=
|=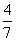 ×2=
×2=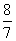
- PはAB上にある。
- ∠Bの2等分線とACの交点をQとするとき、AQの長さ。
角の2等分線 ∠AOBの2等分線上の点をPとすると、  と同じ方向の「単位ベクトル(大きさが1のベクトル)」を
と同じ方向の「単位ベクトル(大きさが1のベクトル)」を 0、
0、
 と同じ方向の「単位ベクトル(大きさが1のベクトル)」を
と同じ方向の「単位ベクトル(大きさが1のベクトル)」を 0、とすれば、
0、とすれば、
「ひし形」の対角線が頂角を2等分することから、
∠AOBの2等分線上の点Pを表す位置ベクトル は次のように表される。
は次のように表される。
 =k(
=k( 0+
0+ 0)
0)
すなわち、
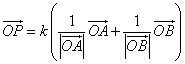
- △OABにおいて、∠AOBの2等分線と辺ABの交点をDとすると、
AD:DB=OA:OBである。
なぜなら、
Oから辺ABに下ろした垂線の長さをhとすれば、
△OADの面積S1,△OBDの面積S2は、 それぞれ次のように表される。
S1= h・AD
h・AD
S2= h・BD
h・BD
したがって、S1:S2=AD:BD
一方、∠AOD=∠BOD=θとすると、
S1= OA・ODsinθ
OA・ODsinθ
S2= OB・ODsinθ
OB・ODsinθ
したがって、S1:S2=OA:OB
以上から、AD:DB=OA:OB
OA=a,OB=bとすると、
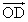 =
=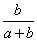
 +
+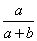

したがって、
 =t
=t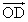 =t(
=t(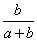
 +
+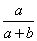
 )
)
-
Qは∠ABCの2等分線上にある。
AB=2,BC=1だから、
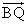 =s(
=s(
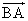 +
+ )
)
始点をAに変えると、
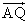 -
- =s{
=s{ (-
(- )+(
)+( -
- )}
)}
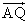 =(1-
=(1-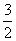 s)
s) +s
+s ・・・①
・・・①
-
QはAC上にあるから、
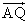 =t
=t ・・・②
・・・②
①②より、 ,
, はいずれも
はいずれも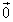 でなく、互いに平行でない(1次独立)から、
でなく、互いに平行でない(1次独立)から、
1-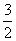 s=0
s=0
s=t
これを満たすs,tは、s=t=
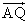 =
=

|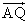 |=
|= |
| |=
|= ×2=
×2=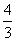
- △ABCの面積。
三角形の面積 △ABCの面積をS、∠BAC=θとすると、
S= AB・ACsinθ
AB・ACsinθ
ここで、0<θ<πだから、sinθ>0
sinθ=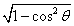
内積の定義から、
 ・
・ =|
=| ||
|| |cosθ
|cosθ
したがって、
S= |
| ||
|| |sinθ=
|sinθ= |
| ||
|| |
|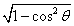
=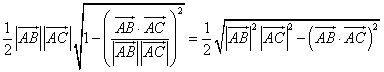
 ・
・ =|
=| |2=4,
|2=4,
 ・
・ =|
=| |2=4,
|2=4,
 ・
・ =
=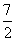 であるから、
であるから、
S=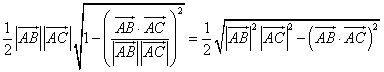 =
=
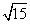
- [例題7]△ABCにおいて、
- ∠ABC,∠BCA,∠CABの2等分線は、1点で交わることを示せ。[内心]
- 辺AB,BC,CAの垂直2等分線は、1点で交わることを示せ。[外心]
- 頂点C,A,Bから、それぞれ辺AB,BC,CAに下ろした垂線は、1点で交わることを示せ。[垂心]
- 外心をO、垂心をHとするとき、以下の式が成り立つことを示せ。
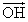 =
= +
+ +
+
さらに、重心をGとするとき、3点G,O,Hは同一直線上にあることを示し、OG:GHを求めよ。
上の定義から明らかなように、重心・外心・内心・垂心のうち、重心以外の3つは、すべて「垂直」という、具体的な「角度」の要素が含まれている。したがって、重心 三角形の3個の頂点と、向かい合う辺の中点を結ぶ線分を「中線」と呼ぶ。
3本の中線は1点で交わる。これを「重心」と呼ぶ。重力の作用する中心だからである。外心 三角形の3個の頂点を通る円はただ一つ定まる。これを三角形の「外接円」と呼ぶ。
外接円の中心を「外心」と呼ぶ。
円の中心から、その「弦」に向かって下ろした垂線は、「弦」を2等分する。
したがって、「外心」は、辺の垂直2等分線の交点である。内心 三角形の3辺に同時に接する円はただ一つ定まる。これを三角形の「内接円」と呼ぶ。
内接円の中心を「内心」と呼ぶ。
内接円の中心から各辺に垂線を下ろすと、その長さはすべてこの円の半径であり、等しい。
したがって、「内心」は頂角の2等分線の交点である。垂心 三角形の3個の頂点から、向かい合う辺に向かって下ろした3本の垂線は1点で交わる。
これを「垂心」と呼ぶ。- 重心は、すべての三角形に共通な、「内積」を用いない表現ができる。[カテゴリー1]
- 外心・内心・垂心の位置は、3個の「内積」の値がわからない限り確定しない。[カテゴリー3]
- [内心]
BC=a,CA=b,AB=cとする。
∠CABの2等分線と、∠ABCの2等分線の交点をIとし、Iが∠BCAの2等分線にあることを示せばよい。
Iは∠CABの2等分線上にあるから、
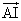 =s(
=s(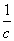
 +
+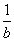
 )
)
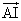 =
=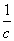 s
s +
+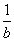 s
s ・・・①
・・・①
Iは∠ABCの2等分線上にあるから、
 =t(
=t(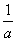
 +
+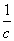
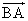 )
)
始点をAに変えると、
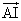 -
- =
=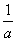 t(
t( -
- )-
)-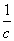 t
t
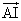 ={1-(
={1-(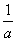 +
+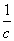 )t}
)t} +
+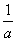 t
t ・・・②
・・・②
①②より、 ,
, はいずれも
はいずれも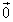 でなく、互いに平行でないから(1次独立)、
でなく、互いに平行でないから(1次独立)、
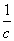 s=1-(
s=1-(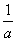 +
+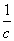 )t
)t
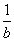 s=
s=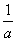 t
t
これらを満たすs,tは、
s=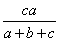 ,t=
,t=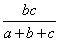
したがって、
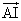 =
=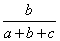
 +
+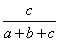

始点をCに変えると、
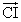 =(1-
=(1-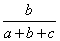 -
-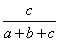 )
)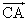 +
+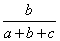
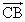
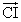 =
=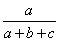
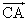 +
+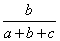
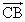
これは次のように変形できるから、
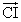 =
=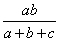 (
(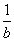
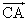 +
+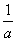
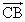 )
)
Iは∠BCAの2等分線上にあることが示された。 - [外心]
-
BCの中点をL、CAの中点をM、ABの中点をNとする。
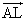 =
=
 +
+

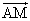 =
=

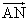 =
=

-
外心Oを表す位置ベクトルを、
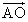 =s
=s +t
+t
とすれば、 -
「外心」は、各辺の垂直2等分線の交点であることから、次の3式が成り立つはずである。
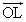 ・
・ =0・・・①
=0・・・①
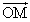 ・
・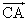 =0・・・②
=0・・・②
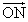 ・
・ =0・・・③
=0・・・③
- 外心の位置を確定するために必要な未知数はs,tの2個であり、これらを規定する条件式が①②③の3個である。
3個の条件式のうちいずれか2個から定まった未知数s,tが、残りの1式をも満たすことを示せば、「3辺の垂直2等分線が1点で交わる」ことが証明されたことになる。 - ②③を満たすs,tが①をも満たすことを示すことにする。
②をAを始点に書き換える。
(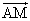 -
-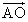 )・(-
)・(- )=0
)=0
{
 -(s
-(s +t
+t )}・
)}・ =0
=0
{s -(
-( -t)
-t) }・
}・ =0
=0
s ・
・ -(
-( -t)
-t) ・
・ =0・・・(ⅰ)
=0・・・(ⅰ)
同様に③をAを始点に書き換える。
(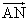 -
-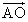 )・
)・ =0
=0
{
 -(s
-(s +t
+t )}・
)}・ =0
=0
{( -s)
-s) -t
-t }・
}・ =0
=0
( -s)
-s) ・
・ -t
-t ・
・ =0・・・(ⅱ)
=0・・・(ⅱ)
一方、①の左辺は、
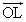 ・
・
={( -s)
-s) +(
+( -t)
-t) }・(
}・( -
- )
)
=-{( -s)
-s) +(
+( -t)
-t) }・(
}・( -
- )
)
=-( -s)
-s) ・
・ -(s-t)
-(s-t) ・
・ +(
+( -t)
-t) ・
・
ここで,(ⅰ)(ⅱ)を用いると、
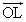 ・
・
=-t ・
・ -(s-t)
-(s-t) ・
・ +s
+s ・
・
=0
こうして、3辺の垂直2等分線が1点で交わることが示された。
-
BCの中点をL、CAの中点をM、ABの中点をNとする。
- [垂心]
-
垂心Hを表す位置ベクトルを、
 =u
=u +v
+v
とすれば、 -
「垂心」は、各頂点から対辺に下ろした垂線の交点であることから、次の3式が成り立つはずである。
 ・
・ =0・・・①
=0・・・①
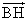 ・
・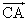 =0・・・②
=0・・・②
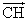 ・
・ =0・・・③
=0・・・③
- 垂心の位置を確定するために必要な未知数はu,vの2個であり、これらを規定する条件式が①②③の3個である。
3個の条件式のうちいずれか2個から定まった未知数u,vが、残りの1式をも満たすことを示せば、「3頂点から対辺に下ろした3個のの垂線が1点で交わる」ことが証明されたことになる。 - ②③を満たすu,vが①をも満たすことを示すことにする。
②をAを始点に書き換える。
( -
- )・(-
)・(- )=0
)=0
{(u-1) +v
+v )}・
)}・ =0
=0
(u-1) ・
・ +v
+v ・
・ =0・・・(ⅲ)
=0・・・(ⅲ)
同様に③をAを始点に書き換える。
( -
- )・
)・ =0
=0
{u +(v-1)
+(v-1) )}・
)}・ =0
=0
u ・
・ +(v-1)
+(v-1) ・
・ =0・・・(ⅳ)
=0・・・(ⅳ)
一方、①の左辺は、
 ・
・
=(u +v
+v )・(
)・( -
- )
)
=-(u +v
+v )・(
)・( -
- )
)
=-u ・
・ +(u-v)
+(u-v) ・
・ +v
+v ・
・
ここで,(ⅲ)(ⅳ)を用いると、
 ・
・
=(v-1) ・
・ +(u-v)
+(u-v) ・
・ -(u-1)
-(u-1) ・
・
=0
こうして、3頂点から対辺に下ろした3個の垂線が1点で交わることが示された。 -
(補)「外心」と「垂心」の関係
上の(ⅰ)(ⅱ)(ⅲ)(ⅳ)が、任意の ・
・ ,
, ・
・ ,
, ・
・ (このうち、
(このうち、 ・
・ 以外は当然0でない)に対して、常に成立するような、s,t,u,vの関係を求めると、計算過程は煩雑なので省略するが、
以外は当然0でない)に対して、常に成立するような、s,t,u,vの関係を求めると、計算過程は煩雑なので省略するが、
u=1-2s
v=1-2t
が得られる。したがって、「外心」Oを表す位置ベクトルを
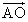 =s
=s +t
+t
とすれば、「垂心」Hを表す位置ベクトルは、
 =(1-2s)
=(1-2s) +(1-2t)
+(1-2t)
すなわち、
 =
= +
+ -2
-2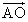
始点をOに変えると、
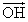 -
- =
= -
- +
+ -
- +2
+2
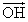 =
= +
+ +
+
これが次の問の「ネタ」である。
-
垂心Hを表す位置ベクトルを、
-
「外心」と「垂心」の関係
-
BCの中点をL、CAの中点をM、ABの中点をNとする。
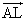 =
=
 +
+

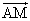 =
=

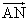 =
=

-
「外心」Oは、各辺の垂直2等分線の交点であることから、次の2式が成り立つ。
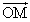 ・
・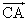 =0・・・①
=0・・・①
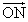 ・
・ =0・・・②
=0・・・②
(
 -
-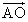 )・(-
)・(- )=0
)=0
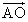 ・
・ =
=
 ・
・ ・・・(ⅰ)
・・・(ⅰ)
②より、
(
 -
-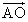 )・
)・ =0
=0
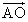 ・
・ =
=
 ・
・ ・・・(ⅱ)
・・・(ⅱ)
-
(ⅰ)(ⅱ)を満たす点O(外心)に対して、与えられた式、
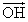 =
= +
+ +
+ ・・・③
・・・③
で示される点Hが、垂心であること、すなわち、BH⊥ACかつ、CH⊥ABであることを示せばよい。
③式の始点をAに変えると、
 =
= +
+ -2
-2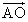
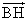 ・
・
=( -2
-2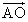 )・
)・
= ・
・ -2
-2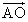 ・
・
=0・・・∵(ⅰ)より
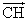 ・
・
=( -2
-2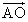 )・
)・
= ・
・ -2
-2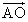 ・
・
=0・・・∵(ⅱ)より
Hは垂心であることが示された。よって、外心O、垂心Hに対して③式が成立する。 -
△ABCの重心Gは、
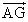 =
=
 +
+

したがって、
 =3
=3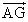 -2
-2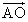
始点をOに変えると、
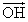 -
- =3(
=3(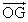 -
- )+2
)+2
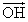 =3
=3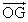
よって、OG:GH=1:2
-
BCの中点をL、CAの中点をM、ABの中点をNとする。
- [例題8]
4点O(0,0,0),A(1,0,0),B(0,1,0),C(0,0,
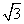 )を頂点とする四面体OABCについて、Oから△ABCを含む平面に下ろした垂線の足をHとするとき、OHの長さ、および、cos∠OAHの値を求めよ。
)を頂点とする四面体OABCについて、Oから△ABCを含む平面に下ろした垂線の足をHとするとき、OHの長さ、および、cos∠OAHの値を求めよ。
[処理手順]- 始点をOとする。
- 1次独立な3個のベクトルとして、
 ,
, ,
, を選ぶ。
を選ぶ。
- その他の点Hを表す位置ベクトル
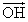 をこれら3個のベクトルで表す。
をこれら3個のベクトルで表す。
- 6個の内積
 ・
・ ,
, ・
・ ,
, ・
・ ,
, ・
・ ,
, ・
・ ,
, ・
・ の値を求めておく。
の値を求めておく。
内積の成分表示 平面 空間 2次元平面ベクトルを、(x,y)座標平面に、
関連付けた表現形式を「成分表示」と呼ぶ。
P(x,y)を表す位置ベクトル を
を
 =(x,y)
=(x,y)
と書く。
x,y方向の「単位ベクトル(長さが1のベクトル)」を
それぞれ ,
, とすれば、
とすれば、
 =(1,0)
=(1,0)
 =(0,1)
=(0,1)
これらの間の内積は、
 ・
・ =1
=1
 ・
・ =0
=0
 ・
・ =1
=1
したがって、
 =(x1,y1)=x1
=(x1,y1)=x1 +y1
+y1
 =(x2,y2)=x2
=(x2,y2)=x2 +y2
+y2
に対して、 ・
・ は、
は、
 ・
・ =(x1
=(x1 +y1
+y1 )・(x2
)・(x2 +y2
+y2 )
)
=x1x2 ・
・ +(x1y2+x2y1)
+(x1y2+x2y1) ・
・ +y1y2
+y1y2 ・
・
=x1x2+y1y23次元空間ベクトルを、(x,y,z)座標空間に、
関連付けた表現形式を「成分表示」と呼ぶ。
P(x,y,z)を表す位置ベクトル を
を
 =(x,y,z)
=(x,y,z)
と書く。
x,y,z方向の「単位ベクトル(長さが1のベクトル)」を
それぞれ ,
, ,
,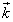 とすれば、
とすれば、
 =(1,0,0)
=(1,0,0)
 =(0,1,0)
=(0,1,0)
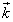 =(0,0,1)
=(0,0,1)
これらの間の内積は、
 ・
・ =
= ・
・ =
=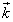 ・
・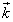 =1
=1
 ・
・ =
= ・
・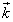 =
=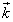 ・
・ =0
=0
したがって、
 =(x1,y1,z1)=x1
=(x1,y1,z1)=x1 +y1
+y1 +z1
+z1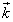
 =(x2,y2,z2)=x2
=(x2,y2,z2)=x2 +y2
+y2 +z2
+z2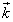
に対して、 ・
・ は、
は、
 ・
・ =(x1
=(x1 +y1
+y1 +z1
+z1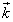 )・(x2
)・(x2 +y2
+y2 +z2
+z2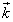 )
)
=x1x2+y1y2+z1z2-
 =(1,0,0)
=(1,0,0)
 =(0,1,0)
=(0,1,0)
 =(0,0,
=(0,0,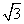 )
)
であるから、これらの間の内積は、
 ・
・ =1
=1
 ・
・ =1
=1
 ・
・ =3
=3
 ・
・ =
=
 ・
・ =
=
 ・
・ =0
=0
- Hは△ABCを含む平面上の点だから、
 =u
=u +v
+v
と表すことができる。始点をOに変えると、
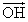 =(1-u-v)
=(1-u-v) +u
+u +v
+v
HはOから△ABCを含む平面上に下ろした垂線の足だから、
OH⊥ABかつ、OH⊥AC
すなわち、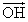 ・
・ =0かつ、
=0かつ、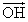 ・
・ =0
=0
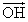 ・
・ =0
=0
{(1-u-v) +u
+u +v
+v }・(
}・( -
- )=0
)=0
{(1-u-v) +u
+u +v
+v }・(
}・( -
- )=0
)=0
 ・
・ =
=
 ・
・ =
=
 ・
・ =0だから、
=0だから、
(1-u-v) ・
・ -u
-u ・
・ =0
=0
1-2u-v=0・・・①
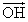 ・
・ =0
=0
{(1-u-v) +u
+u +v
+v }・(
}・( -
- )=0
)=0
{(1-u-v) +u
+u +v
+v }・(
}・( -
- )=0
)=0
 ・
・ =
=
 ・
・ =
=
 ・
・ =0だから、
=0だから、
(1-u-v) ・
・ -v
-v ・
・ =0
=0
1-u-4v=0・・・②
①②より、
u=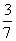
v=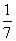
よって、
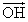 =
=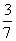
 +
+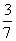
 +
+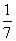

-
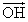 ・
・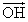 =(
=(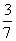
 +
+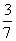
 +
+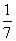
 )・(
)・(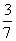
 +
+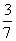
 +
+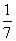
 )
)
=(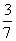 )2+(
)2+(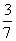 )2+(
)2+(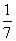 )2×3=
)2×3=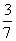
したがって、
|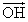 |=
|=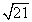 /7
/7
-
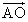 ・
・ =|
=|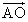 ||
|| |cosθ
|cosθ
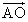 ・
・
=- ・(
・(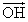 -
- )
)
=- ・(-
・(-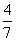
 +
+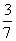
 +
+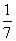
 )
)
=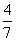
 ・
・ =
=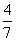
|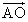 |=|
|=| |=1
|=1
| |2=
|2= ・
・
=(-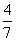
 +
+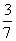
 +
+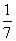
 )・(-
)・(-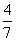
 +
+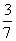
 +
+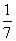
 )
)
=(-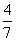 )2+(
)2+(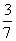 )2+(
)2+(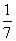 )2×3=
)2×3=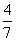
| |=2/
|=2/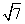
したがって、
cosθ=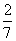
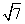
- [例題9]
- 四面体OABCにおいて、△OAB,△OBC,△OCA,△ABCの重心をそれぞれD,E,F,Gとする。線分DC,EA,FB,GOは1点で交わることを証明せよ。
- 四面体OABCは1辺の長さ1の正四面体であるとする。上で求めた、線分DC,EA,FB,GOの交点をP、∠OPA=θとするとき、cosθの値を求めよ。
- [例題4]参照
 =
=
 +
+
 +
+

- OABCは1辺の長さ1の正四面体であるから、6個の内積の値は次のように定まる。
 ・
・ =1
=1
 ・
・ =1
=1
 ・
・ =1
=1
 ・
・ =1×1×cos60°=
=1×1×cos60°=
 ・
・ =1×1×cos60°=
=1×1×cos60°=
 ・
・ =1×1×cos60°=
=1×1×cos60°=
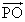 ・
・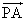 =|
=|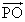 ||
||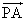 |cosθ
|cosθ
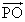 ・
・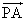 =
= ・
・ =
= ・(
・( -
- )
)
=(
 +
+
 +
+
 )・(-
)・(-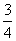
 +
+
 +
+
 )
)
= (-
(-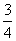 )+(
)+( )2+(
)2+( )2+{(
)2+{( )2+
)2+ (-
(-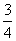 )}×
)}× +2(
+2( )2×
)2× +{(
+{( )2+
)2+ (-
(-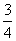 )}×
)}× =-
=-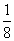
|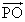 |2=|
|2=| |2=(
|2=( )2+(
)2+( )2+(
)2+( )2+2(
)2+2( )2×
)2× +2(
+2( )2×
)2× +2(
+2( )2×
)2× =
=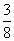
|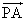 |2=(
|2=(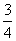
 -
-
 -
-
 )・(
)・(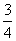
 -
-
 -
-
 )
)
=(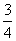 )2+(
)2+( )2+(
)2+( )2-2
)2-2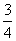

 +2(
+2( )2
)2 -2
-2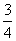

 =
=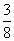
|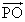 |=|
|=|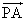 |=
|=
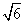
cosθ=-
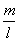 (x-x0)
(x-x0)
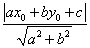
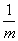 (y-y0)=
(y-y0)=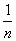 (z-z0):yz平面に平行な直線
(z-z0):yz平面に平行な直線
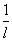 (x-x0)=
(x-x0)=