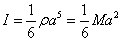• 慣性モーメントの定義
  質点系を構成する質点P_iの質量をm_i、P_iと定直線lとの距離をr_iとするとき、直線lについてのこの質点系の｢慣性モーメント｣Iは、
  
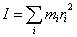
  質量が連続的に分布しているときは、この物体の密度ρを用いて、
  
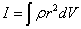
  すなわち
  
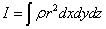
  と定義される。
• 固定軸まわりの回転運動の基本方程式
  運動方程式
  
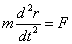
  すなわち、
  
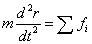
  ｢外力の合力がゼロでないとき、これに比例した加速度が発生する｣
  に対して、
  
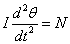
  すなわち、
  
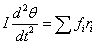
  ｢外力のモーメントの和がゼロでないとき、これに比例した角加速度が発生する｣
  と読み替えることによって、「固定軸まわりの回転運動の基本方程式」を得ることができる。
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
• 半径R、高さL、質量mの円柱の、底面の円の中心を通る軸まわりの慣性モーメント
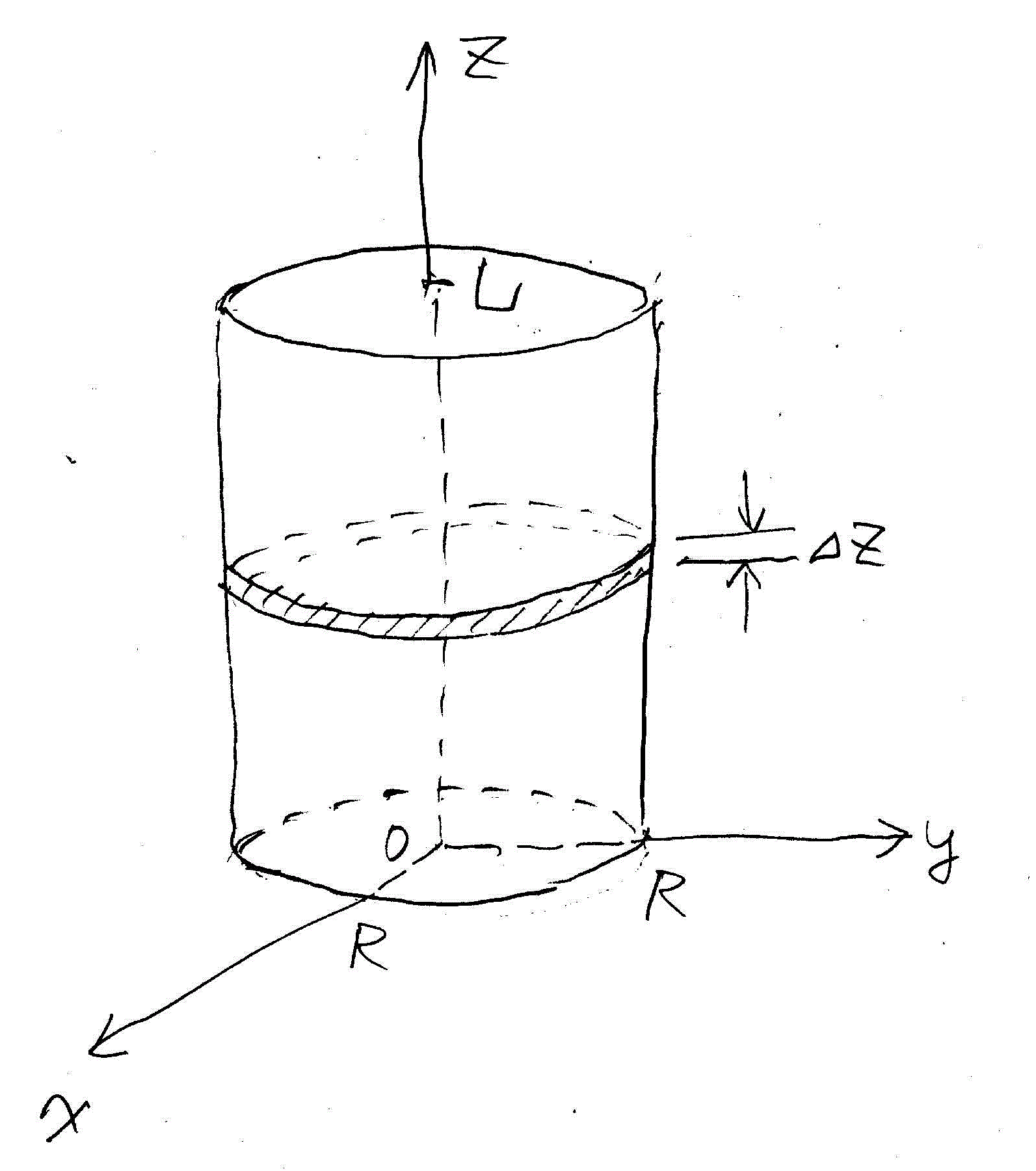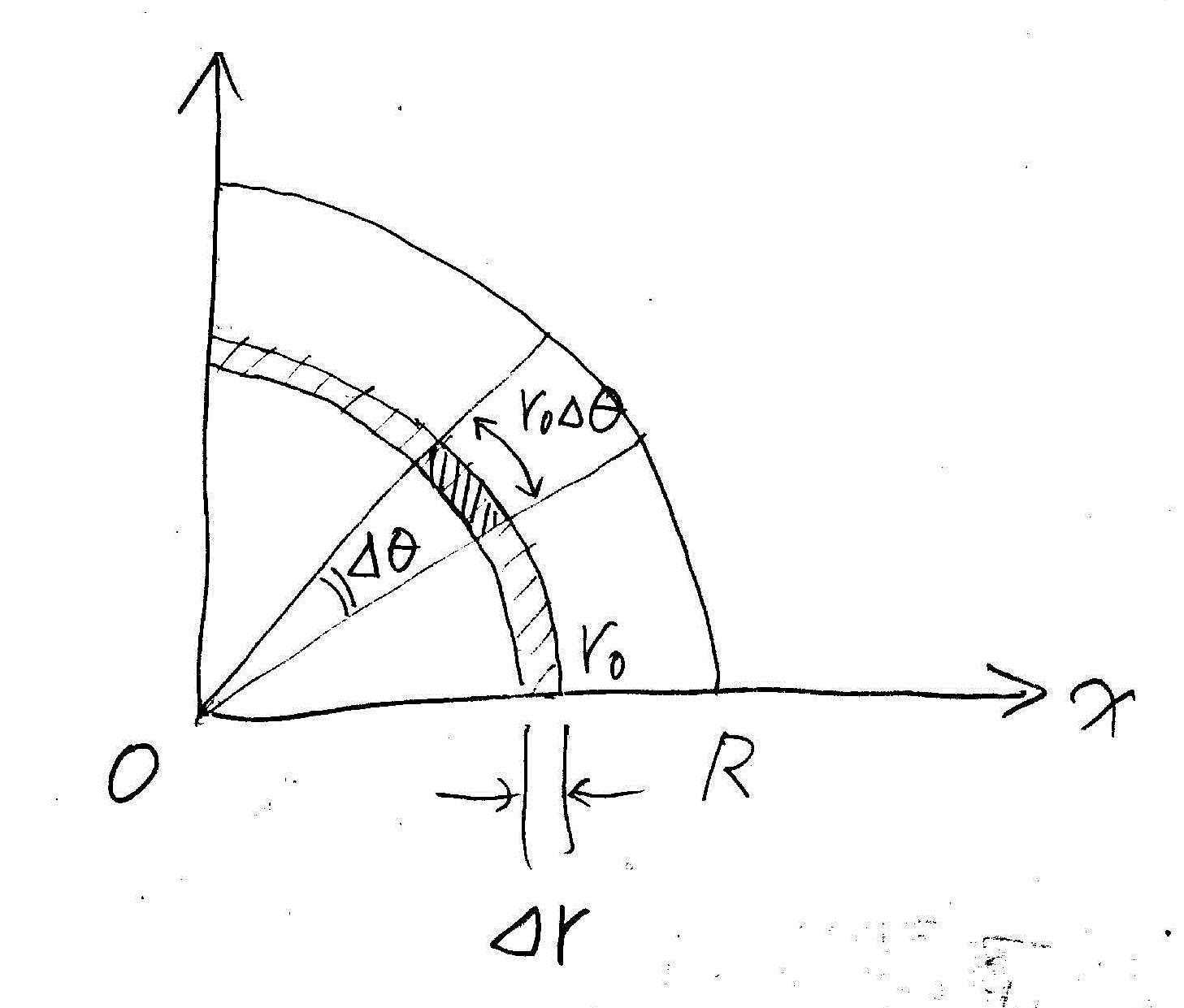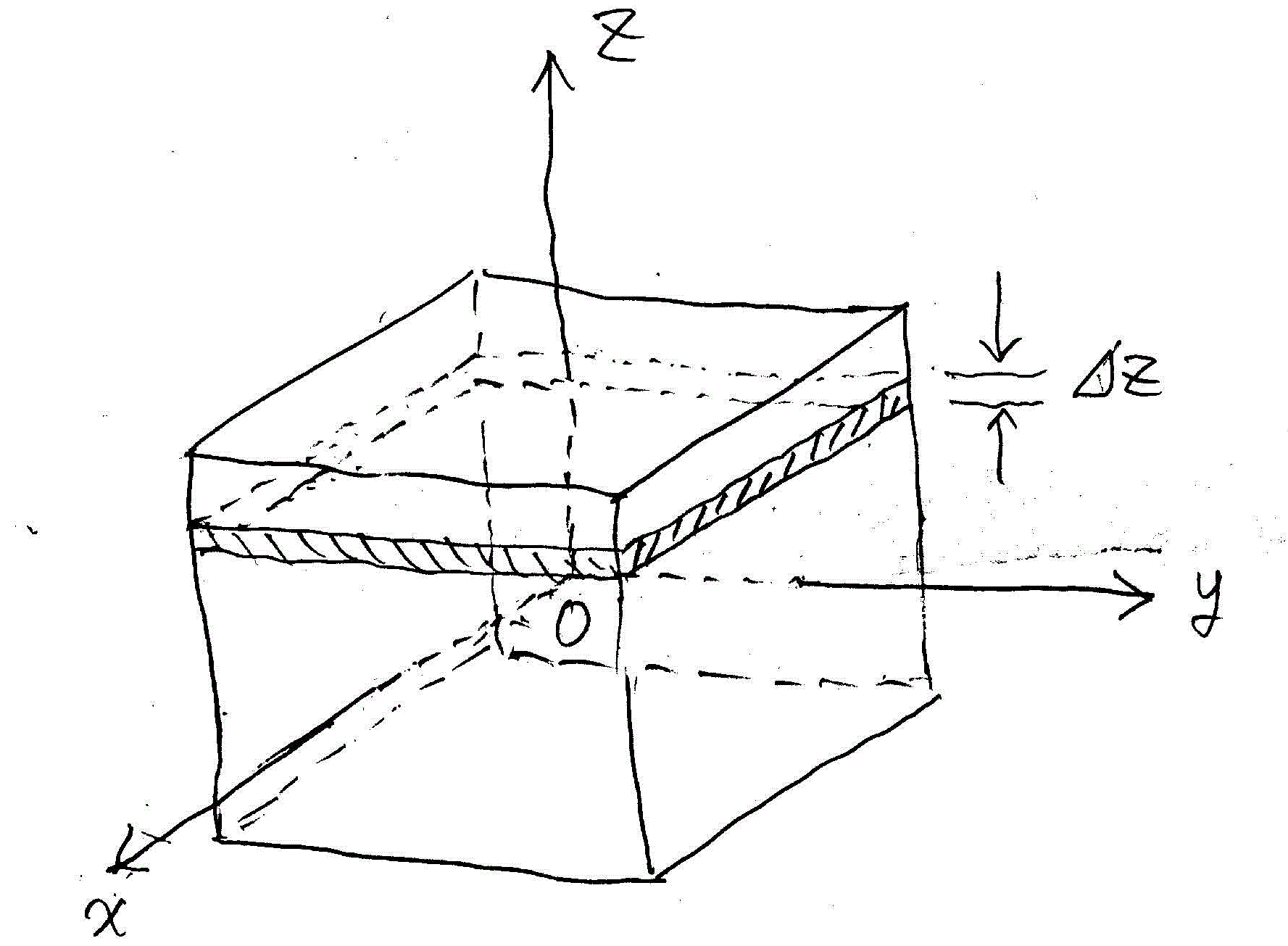
  • 図のように座標軸をとり、z軸方向の微小厚さzの円柱板を切り出す。
  • x-y平面は極座標をとる。r=r₀にある微小幅rの｢ドーナツ｣状の立体を考え、
  • さらに微小角度θ部分を切り出す。
  • この微小部分は、縦、横、高さがそれぞれ、r、r₀θ、zの直方体に近似できる。
  • 密度をρとすれば、その質量はρr₀rθz、軸までの距離がr₀であるから、
  • この微小な直方体が軸に対してもつ慣性モーメントの寄与分は、ρr₀³rθz
  • まず、θについて積分。
    
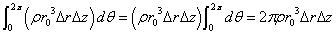
  • 次に、定数r₀を変数rと読み替えて、rについて積分。
    
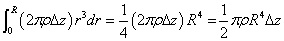
  • 最後に、zについて積分。
    
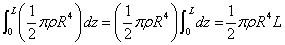
  • ここで、m=ρπR²Lであるから、
    
  
  
  
  
  
  
  
  
  
  
  
  
  
• 一辺の長さa、質量Mの立方体の、向かい合う二面の対角線の交点を通る軸まわりの慣性モーメント
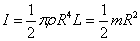
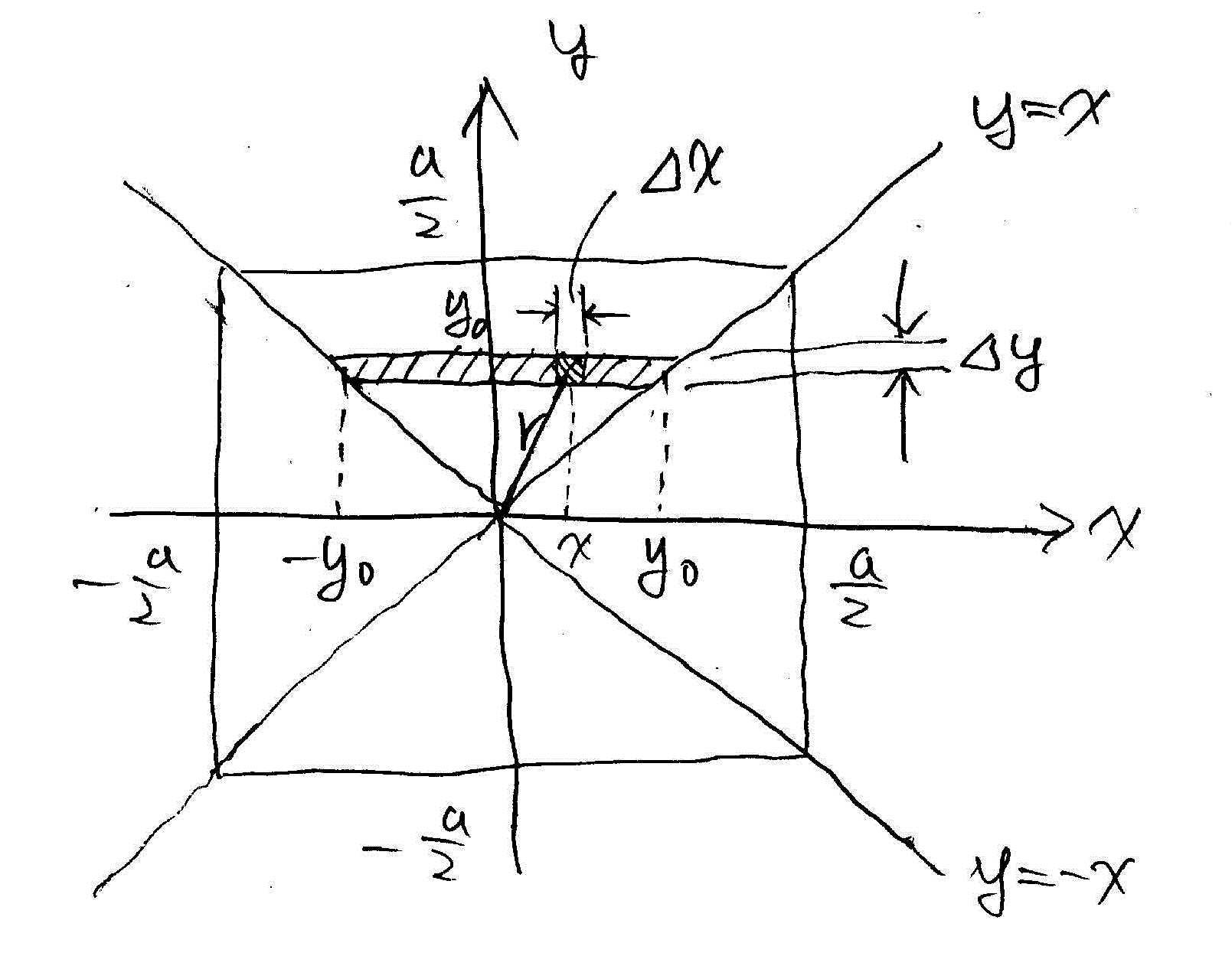  • 図のように座標軸をとり、z軸方向の微小厚さzの四角柱板を切り出す。
  • r=y₀にある微小幅yの長方形を考え、
  • さらにxの位置にある微小部分xを切り出す。
  • この微小部分は、縦、横、高さがそれぞれ、x、y、zの直方体である。
  • 密度をρとすれば、その質量はρxyz、軸までの距離が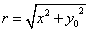であるから、
  • この微小な直方体が軸に対してもつ慣性モーメントの寄与分は、ρ(x²+y₀²)xyz
  • まず、xについて積分。
    
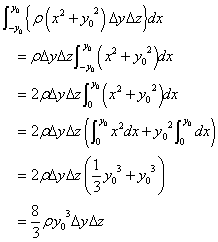
  • 次に、定数y₀を変数yと読み替えて、yについて積分。
    
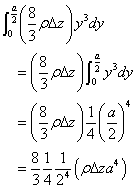
  • 図形の対称性からこれを4倍したのち、最後に、zについて積分。
    
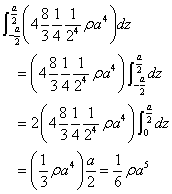
  • ここで、M=ρa³であるから、