・・・
すなわち、
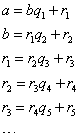
したがって、有理数a/bは、次のように連分数で表示できる。
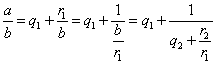
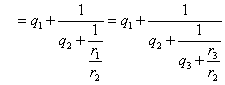
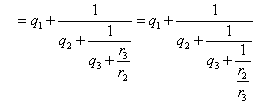
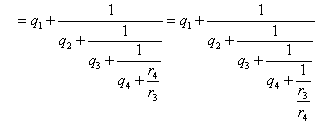
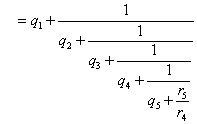
これは、どこでとめても、完全に正しい等式である。
πを、まず、1で割ることからはじめる。
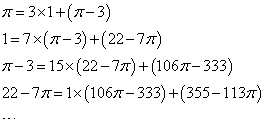
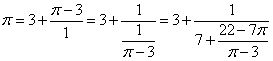
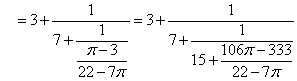
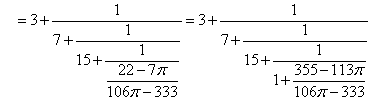
こうして、πの連分数による近似表示ができたことになるが、何か「騙された」(笑)ような気がしませんか?
私たちは、は・じ・め・か・ら・πの正確な値を知っているからこそ、
たとえば、上式で、π-3を22-7πで割ったら商は15である、などと言えるのだ。
これは「循環」というべきだろう?
この世では・じ・め・て・πの連分数表示を発見した人は、いったい、どうやったんだろうね?
これに比べると、Atan(x)のマクローリン級数展開を用いた、πの近似式のほうは、収束は遅いけれどもtan(π/4)=1である、という事実しか使っていないから、「いかさま」(笑)感は小さい。
でも、では、どうしてAtan(x)の微分の仕方を知・っ・て・いるのだ?、と問われたならば、いや、知っていたからだ(笑)、と答えざるを得ないから、やはり、どこかで、「循環」は、しているのである。
パーソナルコンピュータの精度は意外に(笑)小さくて、πの小数点以下は、
「エクセル」では3.14159265358979で14桁、
「BASIC」でも 3.14159265358979324で17桁、
までしか表示できない。だから、連分数表記も、「エクセル」なら3回、「BASIC」でも4回まで。それ以降は誤差の範囲に入ってしまって、無意味な計算になる。
100 dim s(4)
110 a=3.1415926535897932384626
120 x=a
130 p=1
140 for k=1 to 4
150 q=int(x/p)
160 r=x-p*q
170 print q
180 s(k)=q
190 x=p
200 p=r
210 next
215 print
220 print s(1)
230 print s(1)+(1/s(2))
240 print s(1)+(1/(s(2)+(1/s(3))))
250 print s(1)+(1/(s(2)+(1/(s(3)+(1/s(4))))))
300 end
3
7
15
1
3
3.14285714285714286
3.14150943396226415
3.1415929203539823
OK
つまり、
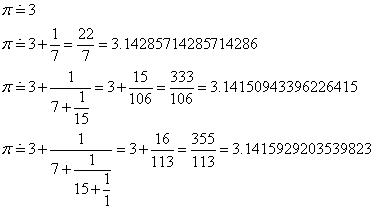
となって、たった4回の操作でも、小数点以下6桁まで、あっている!