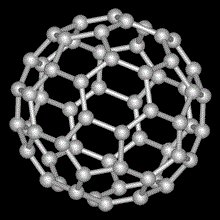
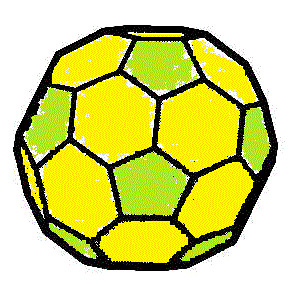
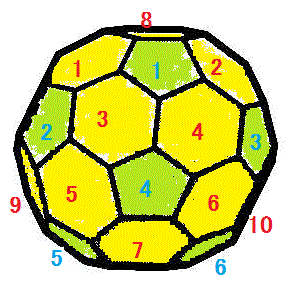
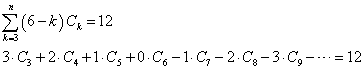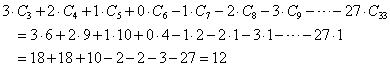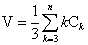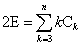この世に、凸・正多面体は、下の5種類しか存在しない。どうしてそんなことが断定できるのだ?
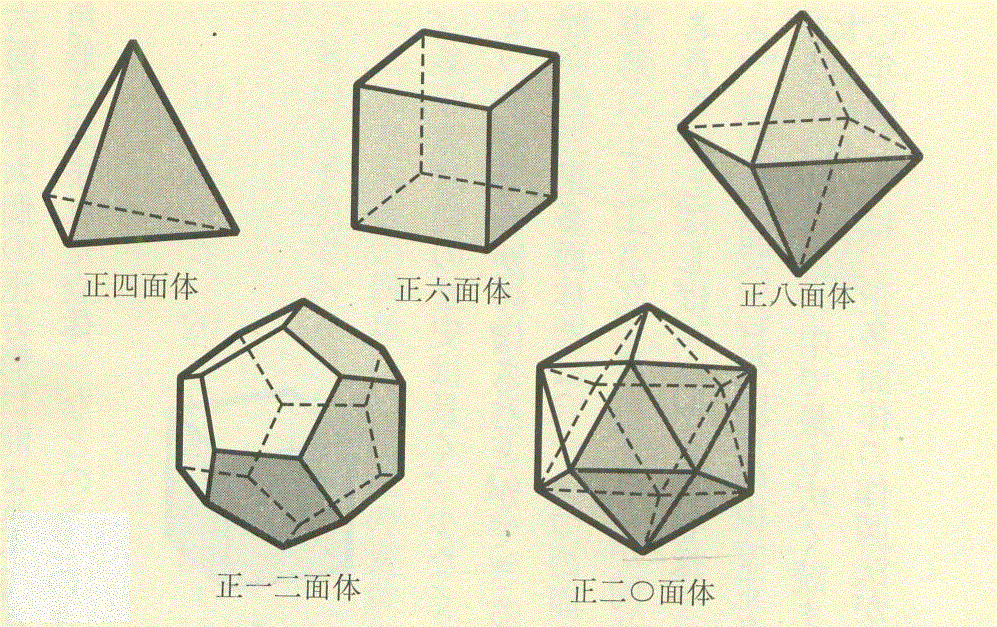
正多面体は、全ての面が正多角形で出来ている。その頂点には従って、いくつかの正多角形の頂点が集まっているわけだ。いくつまで集まることができるか?、には、自ずと、制限がある。
上の5つの図を見るに、
- 各面が、正三角形、で出来ているものが、正四面体、正八面体、正二十面体、の3つ、
- 各面が、正四角形、つまり正方形、で出来ているものが、正六面体、つまり立方体、1つ、
- 各面が、正五角形、で出来ているものが、正十二面体、1つ、
- 正四面体、正六面体、正十二面体では、3つ、これを「三岐」正多角形、
- 正八面体では、4つ、これを「四岐」正多角形、
- 正二十面体では、5つ、これを「五岐」正多角形、
ところで、多面体が「凸である」、「尖っている」、とは、どういうことだ?、裏から見ればそれは「凹である」、「へこんでんでいる」ことではあるが、・・・。厚紙を切り抜いて、円錐を作ろうと思えば、その側面の展開図は扇型で、その中心角は、もちろん決して360度になることはなく、360度より小さければ小さいほど、「尖った」円錐が得られるであろう。
これを類推すれば、一つの頂点に集まる正多角形の頂角の和が360度以上であってはならない、ということなのだな。
ところで(笑)、立体であるためには、少なくとも「三岐」でなければならない。たった二つの平面図形が出会っただけならば、それは、やはり、平面でしかない(笑)、奇しくも、やはり立体は「3次元」なのであった。
従って、「制限」は、次のように定式化できる。凸・正多面体を構成する、正多角形の一つの内角は、少なくとも3倍して360度以上になるものであってはならない。つまりひとつの内角が120度未満の正多角形しか、正多面体は構成できない!
ところで、正多角形のひとつの内角は、どうやって求めるんでしたっけ?、一般に、凸n角形は、頂点がn個あるから、そこから引き得る対角線数は、自分自身と両隣を除いて、(n-3)、これらの対角線によって、凸n角形は、それよりひとつ多い、(n-2)個の三角形に分割できる。三角形の内角の和は180度であるから、内角の和は180(n-2)、凸・正n角形の一つの内角は、これをn等分すればよいから、180(n-2)/n、
では、三角形の内角の和が180度、どうやってわかったんだよ?、なんか、紙に書いた三角系をちぎって並べたら直線になった、みたいな証明しか思い出せなくて気持ち悪いから(笑)、もう一つ別のアプローチ、凸・n角形の「外角」をすべて加算すると、360度になる。これは、その図形上を、例えば反時計回りに「歩いてみる」ところを想像してみれば良い。角に来るたびに、あなたは、左向きに、曲がる。その曲がる角度は、その頂点の外角の大きさに等しい。それを繰り返して一周終えれば、あなたは、元の位置に、元と同じ向きに立っている。つまり、あなたは、360度、だけ、回転したはずなのである。凸・正n角形であったならば、ひとつの外角は、こうして360/nとなる。内角は、180度からこれを引けばよいから、180-360/n=180(n-2)/n。
いずれにしても、
180(n-2)/n<120
180(n-2)<120n
60n<360
n<6
確かに、正五角形までしか無理であることがわかった。なるほど、正六角形では、「蜂の巣」、C黒鉛分子の一層の構造、ベンゼン環が二つ三つつながった有機化合物はなんと言いましたっけ?、・・・、いずれも、平面なのである。正六角形だけでは「立体」を構成できない、だから(笑)、サッカーボールも、C60フラーレンも、正六角形に、ところどころ、正五角形を「混ぜた」のだな?
- 正三角形の一つの内角は、60度。60×m<360の自然数解で3以上のものは、m=3,4,5、だから、「三岐」、「四岐」、「五岐」が可能で、それぞれ、正四面体、正八面体、正二十面体となり、
- 正四角形、正方形の一つの内角は、90度。90×m<360の自然数解で3以上のものは、m=3のみ、だから、「三岐」しかなく、正六面体、すなわち立方体、
- 正五角形の一つの内角は、108度。108×m<360の自然数解で3以上のものは、m=3のみ、だから、やはり「三岐」しかなく、正十二面体となる。
こんなことも知らずに、私は「数学の先生」をやっていたわけだが(笑)、もう済んだことだし、特に悔いもなければ「反省」もしない。
「オイラーの贈物」吉田武(ちくま学芸文庫)、というとても優れた書物があって、eiπ=-1を導くために、すべての必要な素養をとても簡明に説明してくれているのだが、文庫版は絶版で、今年数学の先生になる筈の人に、プレゼントしたい、などと「うつ病患者」らしからぬ「積極性」を発揮して、「Amaz●nマーケットプレイス」を探索していたところ、・・・、同じく「オイラーの公式」、と呼ばれる、多面体の、面・辺・頂点数に関する「公式」の関係で、「四色問題」R・ウィルソン(新潮文庫)をヒットしてしまった。
昨年の10月頃、私は、生徒から聞きかじったおぼろげな話から、その歴史的に有名な数学上の難問に、没頭していた。
世界を塗り分ける。
無限を「回収」する球体。
または、三叉路には魔物が住むのだ。
つもりだったのだが、どうやらそれは、いわゆる「四色問題」とは、命題論理的には、「逆」の関係になる、「メビウスの五人の王子問題」であったかもしれない。で、当分、その話をする。あれ?、正規分布確率密度関数は、どうなった?
| 面の数F | 辺の数E | 頂点の数V | |
| 正四面体 | 4 | 3×4÷2=6 | 6×2÷3=4 |
| 正六面体 | 6 | 4×6÷2=12 | 12×2÷3=8 |
| 正八面体 | 8 | 3×8÷2=12 | 12×2÷4=6 |
| 正十二面体 | 12 | 5×12÷2=30 | 30×2÷3=20 |
| 正二十面体 | 20 | 3×20÷2=30 | 30×2÷5=12 |
面faces、辺edges、頂点vertices、だそうだから、それぞれの頭文字を変数名にして、
さらに、各正多面体を構成する正多角形が、正三角形、正方形、正五角形であったから、その3,4,5を表す変数を、芸がないが(笑)xにでもして、
さらに、「三岐」、「四岐」、「五岐」の3,4,5を表す変数を、yとしよう。
- E=x×F÷2、面の数だけ正多角形がある、ところがそのままかけたら、辺というものは、隣接する二つの面に共有されているのだから、二回ずつ重複して数えていることになるから、2で割る。
- V=E×2÷y、辺の両端に、つまり1辺に対して2個ずつ頂点がある、ところがそのままかけたら、頂点は、接合した各面に共有されているのだから、その分だけ重複して数えていることになるから、変数yで割る。
F+V=E+2
なるほど、不気味なことに(笑)、成立しているのである。
立体の図を眺めて、辺や頂点を「数える」のは大変だが、ここでも、「位相同型的変形」、が役に立つ。これらの立体の各辺が、ぐにゃぐにゃに伸び縮みできるゴム状のものと想像して、「潰して」見る。そうして一旦平面になってしまったら、不思議なことに、とても数えやすいのである。
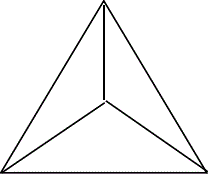
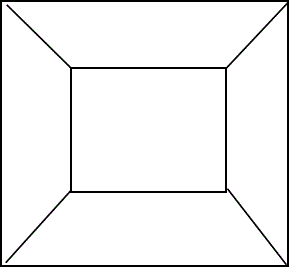
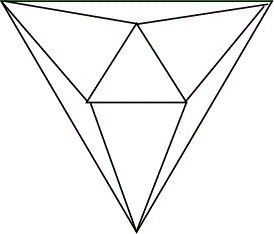
正十二面体までで、飽きたので(笑)、終了。
上の、面の数F、辺の数E、頂点の数Vの表は、なかなか興味深い。「オイラーの公式」からは、話は逸れてしまうが、頂点数が気になった。正六面体が8個で、正八面体が6個、正十二面体が20個で、正二十面体が12個、とは、なんだか不気味な入れ替えが生じているではないか?
金平糖、今の人たちはそんなもの見たこともないだろうが、多分、砂糖の高濃度溶液中に、なにか結晶の核になるようなものを糸の先か何かにつけて、ゆっくりと結晶形成させるのだと思う。そうすると、球体の表面に、規則的なデコボコのあるお菓子ができる。夏目漱石の「弟子」の物理学者、寺田寅彦が随筆の中で、この話をして、確率論の「理由欠乏の原理」に言及していた。今日的には「エルゴード性」というのに対応した言い方だと、勝手に解釈しているが、・・・、例えば、サイコロを振って「6」の目が出る確率が、1//6である「積極的」な、根拠は、ない(笑)、ただ、サイコロ、なる正六面体を眺めてみて、どの面にも、とくに出やすい「理由」がな・い・から、「やむなく」すべての場合の数6の逆数を以て、「確率」と、呼んだのである。
正凸多面体は、空間に、いずれも「とくに区別する理由がな・い・」形で展開している。例えば正十二面体の20個の頂点を、その中心、それが外接する球体の中心、ということだが、に立っている人は、区別することができない。こちらが天でこちらが地、こちらが東でこちらが西といった空間の「偏り」を導入しない限り、すべての頂点は、「あなた」から、等距離にある。そうか!、だから、「区別ができない」、から、なにか「しるし」でも付けない限り、「数える」ことが困難なのだ。
自然界に、正凸多面体のサンプルがいくつも見出されるのも、これで説明できる。海底にあまり敏速に動けない形で定着するウニは、全ての方向からの危険に対処しなければならないから、どの方向にも、均等な密度で刺を生やす。シマキツネノボタン(キンポウゲ科)という花は、「金平糖」とそっくりの果実を作るのだが、これに限らず、多くの植物の果実が、「球形」であるのは、とくにどの方向かに細胞分裂を活発化させる「理由」がなかったのだ、と想像できる。
炭素原子は、最外殻電子数が4で、通常は(笑)、4方向に共有結合する。その4方向には、「とくに区別する理由がない」とき、は、どの方向にも対等に広がり、正四面体構造をとる。CH4メタンなる物質も、ダイヤモンド結晶の一構成単位も、正確に正四面体であることが知られている、らしい(笑)。私たちを含む、この惑星上の全ての生き物は、その身体を構成するタンパク質のユニットとして、炭素原子の周りに4つの様々な「基」が結合したわずか20種ばかりのアミノ酸、というものを共有している。「基」の静電気的特性によって歪みが生ずるから、正確なものではないが、やはり正四面体類似の構造が、延々と接続して、「私たち」の身体は構成されているのである。
この世の、今度は「無生物」に目を転じると、「土」、の主要な構成元素はケイ素、やはり、最外殻電子数4の四面体構造をとるケイ酸塩が、主成分なのである。
この符合が偶然であるはずはないので、やはり「この世で」最も硬い物質がダイヤモンドであることからも、例えば「古代人」は、3本の木材の一方を束ねて、三角錐状の住居をこしらえたに違いないことからも、「正四面体」というものが最も力学的に堅固な構造を与えるものであったからこそ、それが、生物界でも、無生物界でも、「選ばれた」、というべきなのだろう。
ところが炭素原子は、なにかの都合で(笑)、四方向ではなく、三方向、二方向にしか結合しない場面があって、三方向ならば、黒鉛分子、ベンゼン、エチレン、のように平面構造をとる。二方向ならば、アセチレン分子や、二酸化炭素分子のように、直線構造をとる。誰も現に「見た」ことのない話を得意そうにするのは気が引けるが、どうもそうであるらしいので、寛恕願いたい。どうして、そうなるのか?、
- 一つの点から、4本の全く対等な線分が出る。その他端の4点は、正四面体の頂点のように配置せざるを、得ないだろう?
- 一つの点から、3本の全く対等な線分が出る。その他端の3点は、互いに120°の角度をなして正三角形の頂点のように配置せざるを、得ないだろう?
- 一つの点から、2本の全く対等な線分が出る。その他端の2点は、互いに180°の角度をなして、もとの点とともに直線をなさざるを得ないだろう?
正凸n面体は、一つの点から、n本の全く対等な線分が出る、わけで、では、その隣接する2本の線分のなす角は?、と、調べてみたくなるのが人情で、正六面体、つまり立方体、正八面体、正二十面体について、やってみた。正八面体は、明らかに90度、であるが、はてさて、希望通りの(笑)、「法則性」が得られたかどうか?、今日はもう、「飽きた」ので、このへんで。
一辺2の正六面体、立方体の8個の頂点を、(1,1,1)、(1,-1,1)、(-1,1,1)、(-1,-1,1)、(1,1,-1)、(1,-1,-1)、(-1,1,-1)、(-1,-1,-1)、としよう。
どれも「とくに区別する理由がない」、対等な関係であることは分かっている(笑)から、隣接する、つまり、最短距離の2点として、(1,1,1)と(1,-1,1)を選ぶ。
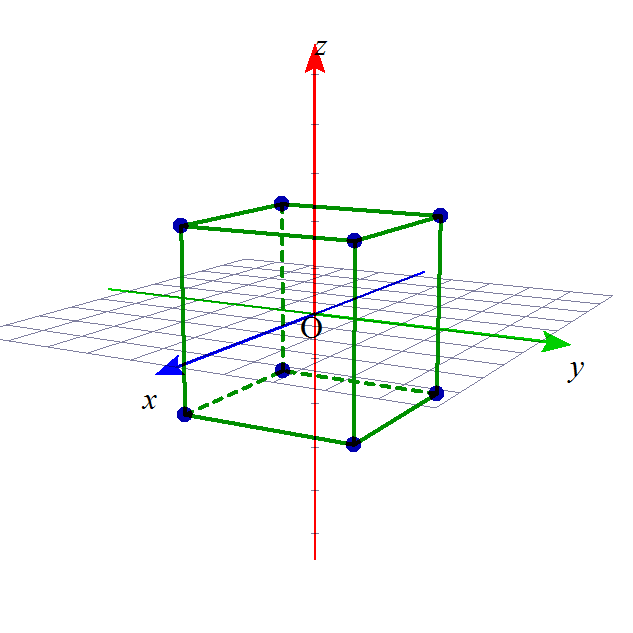
ベクトルu=(1,1,1)、v=(1,-1,1)、と名付ける。「内積」を計算すると、
u・u=1×1+1×1+1×1=3
v・v=1×1+(-1)×(-1)+1×1=3
u・v=1×1+1×(-1)+1×1=1
従って、|u|=√3、|v|=√3、これら二つのベクトルのなす角をθとすれば、
u・v=|u||v|cosθであるから、cosθ=1/3となった。
| 一点から発する線分の数 | 対応する正凸多面体 | 最も近い2線分のなす角の余弦 |
| 2 | (直線) | -1 |
| 3 | (正三角形) | -1/2 |
| 4 | 正四面体 | -1/3 |
| 6 | 正八面体 | 0 |
| 8 | 正六面体 | 1/3 |
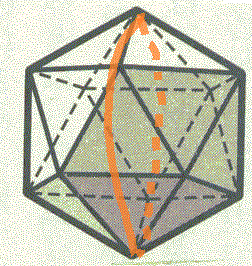
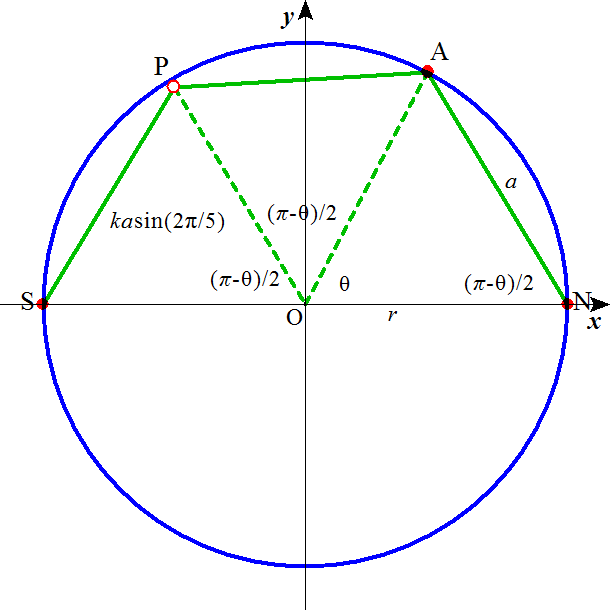
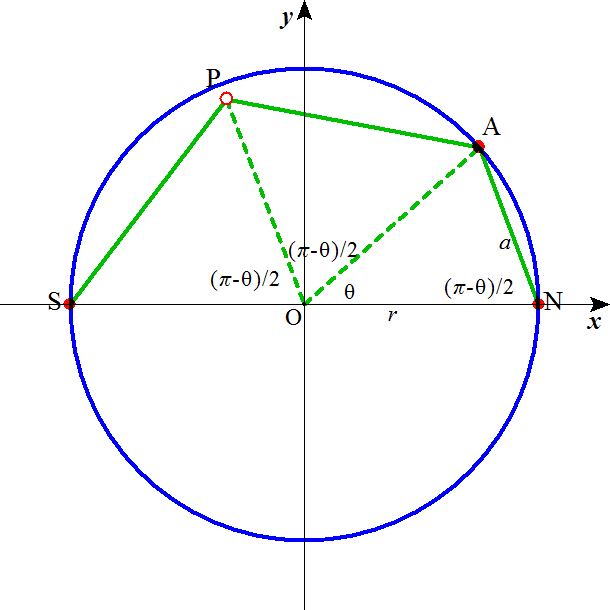
次に頂点数が少ないのは、正二十面体の12である。下図のように、外接円、ところで、正凸多面体はことごとく球に内接する、どうしてそんなことが言えるのだ?、ここでも「理由欠乏の原理」が役に立つ、「とくに偏っている理由がない」から、正凸多面体の各頂点は、どこか、ある「真ん中の」点から、等距離にあるはずなのである、・・・、その必ず接しているはずの外接円の「大円」をとり、「てっぺん」、「北極」ということで、Nとしよう、から、図の「手前」側を通り、最下点、「南極」Sに到り、今度は裏側へ回って「てっぺん」に向かっていくと、この「大円」は、正三角形の一辺、正三角形の頂角の二等分線2個、また、正三角形の一辺、正三角形の頂角の二等分線2個、を含んでいる。
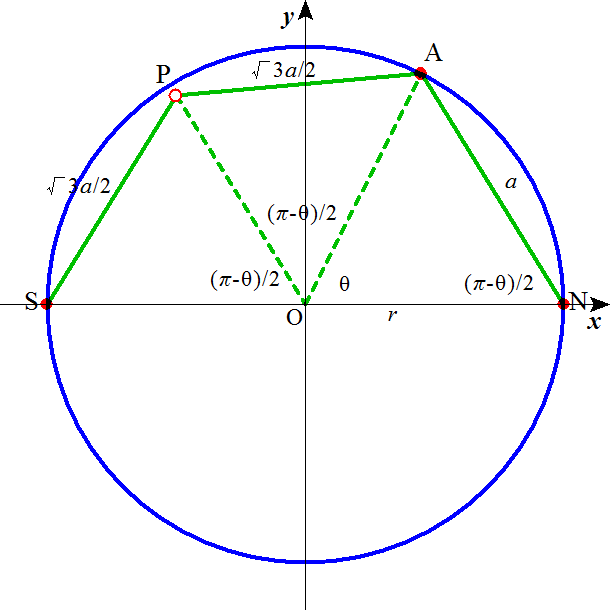
その断面を切り出すと、下図のようになろう。ひとつめに通過した正三角形の頂点をAとする。次の二つの正三角形の頂角二等分線の交点Pは、大円の円周上にはない。求めたいのは、弧NAに対する中心角θである。外接円の半径r、表面の正三角形の一辺aとすると、△ONAはON=OA=r、AN=aの二等辺三角形だから、∠ANO=(π-θ)/2、AP、SPはともに一辺aの正三角形の頂角二等分線であるから、その長さはasin60°で√3a/2、△APOと△SPOは合同であるから、∠AOP=∠SOP、この角もやはり(π-θ)/2である。これを計算の便宜のために、φとおくことにしよう。
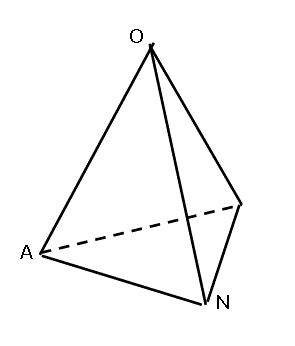
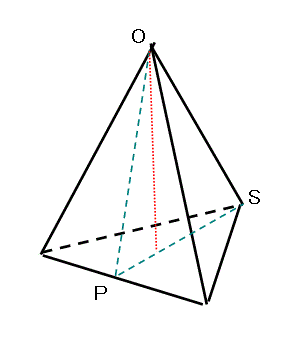
正二十面体の各頂点と、外接円の中心とを結んだら、20個の正三角錐、底面は一辺aの正三角形、側面はa、r、rの二等辺三角形、に切り分けられるはずだ。それを切り出してみた。
最終目標は、cosθを、aもrも含まない「数」として表現することだが、その前提として、θとrを、aの関数として表現しなければならない。条件式は二つ必要である。
- △OANは、この三角錐の側面であるから、
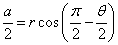 ・・・(1)
・・・(1)
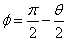 とおいたから、a=2rcosφ
とおいたから、a=2rcosφ
- 右図において、PSの長さが、一辺aの正三角形の頂角二等分線の長さ√3a/2であること、これが二つ目の条件になる。
OPは、側面の二等辺三角形の頂角二等分線であるから、OP=rsinφ、∠POS=φであるから、「余弦定理」を用いて、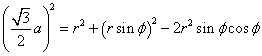 ・・・(2)
・・・(2)
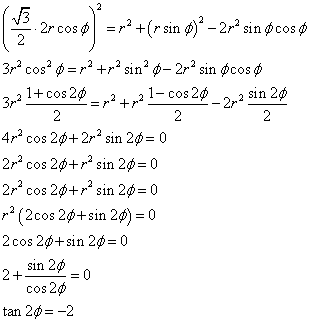
ここで
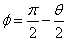 であったから、θ=π-2φ、すなわち、2φ=π-θ、
であったから、θ=π-2φ、すなわち、2φ=π-θ、
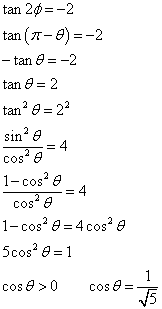
ちなみにθの値を度数法で表すと、63.43494882・・・ということで、正三角形の一つの角よりは、少し広いのであった。
| 一点から発する線分の数 | 対応する正凸多面体 | 最も近い2線分のなす角の余弦 | 最も近い2線分のなす角 |
| 2 | (直線) | -1 | 180 |
| 3 | (正三角形) | -1/2 | 120 |
| 4 | 正四面体 | -1/3 | 109.4712206 |
| 6 | 正八面体 | 0 | 90 |
| 8 | 正六面体 | 1/3 | 70.52877937 |
| 12 | 正二十面体 | 1/√5 | 63.43494882 |
20個の頂点を持つ正十二面体、同じように大円で切る。正五角形の一辺と、同じ正五角形を縦に真っ二つに分割する線分が二本、その半円の中に登場するようであるから、まず、正五角形の辺と対角線の関係、言うまでもなく(笑)「黄金比Golden_Ratio」問題に言及すべきこととなる。
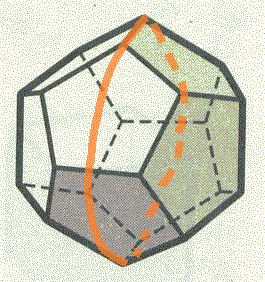
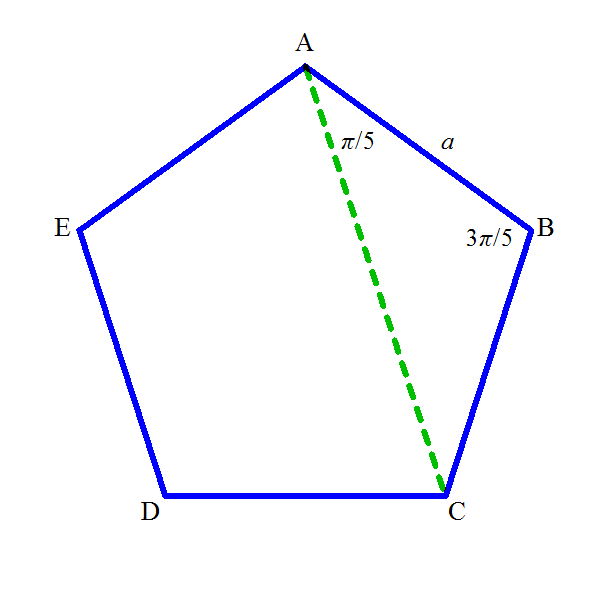
正五角形ABCDEの一辺ABに対する、対角線ACの比を「黄金比」と呼ぶ。その縦横比を持った長方形が、視覚に最も「心地よく」感じられ、だから古来多くの建築物、絵画作品に採用されてきたのだ、と言うが、やはり何度聞いても信じがたい。この数字の持つ「魔術的」なオーラが、人々の無意識に働きかけ、・・・、などというとますます怪しげではあるが、事実として、「不気味な」数なのである。
正五角形の一つの内角は、(5-2)π/5=3π/5すなわち108°、ならば二等辺三角形△ABCの残りの角はπ/5すなわち36°。この正五角形の外接円の半径をrとして「正弦定理」を適用すると、
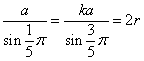
ここに、kが、ACのABに対する比、すなわち「黄金比」である。すなわち、
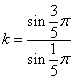
計算の便宜のために、ここでα=π/5とおくと、
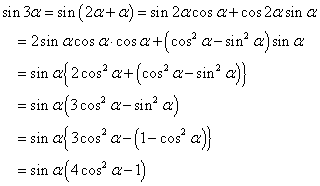
であるから、
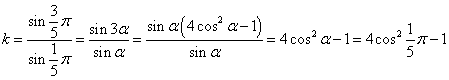
を求めるのが当面の目標である。
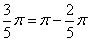 という当然の理屈から、
という当然の理屈から、
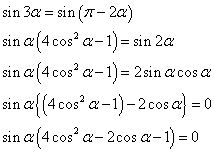
当然sinα≠0であるから、カッコの中が0になるはずである。ここでX=2cosαとおけば、
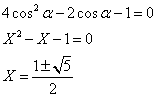
X>0だから、
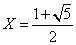
ところで、「黄金比」kは、
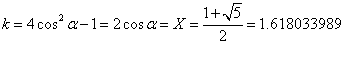
同じ結果は、ベクトルを用いて、三角関数を一切用いることなく、得ることができる。正五角形を対角線によって切ると、二等辺三角形と等脚台形に分割できる。その等脚台形の下底の上底に対する比が、すなわち「黄金比」kであるから、たとえばAC=kEDと書ける。これらを用いて、ベクトルAB及びAEなる「基底」、1次独立な2個のベクトルの組、を用いて、たとえばベクトルADを二様に表現し、表現の「一意性」からそれぞれの係数が等しくなければならない、という根拠から、もちろん、同じ結果を得る。
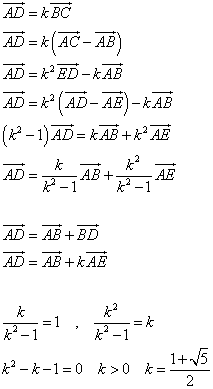
ジャック・ラカンは、「黄金比」に次のような「意味」を与えている。ラカンは、3ページ以上読んだことはない(笑)。岩波新書のタイトルは忘れた、新宮一成の書物から仕入れた「ネタ」。
- 「私x」が「他者y」に注ぐ「まなざし」をy/xなる分数で表記し、
- 「私x」と「他者y」をともに含む「世界x+y」が、「私x」に注ぐ「まなざし」、x/(x+y)、が、
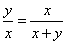
「世界」が、「私」の何倍なのか?(笑)、つまり、「私」は「他者」より、どれほど大きいのか?、x/yに、例えばcという「名」を与えれば、
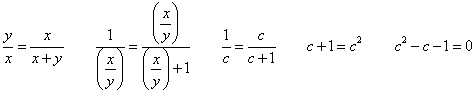
と、全く同型の方程式を得る。「世界」は「私」の、約1.6倍である。同時に、「私」は、「私」以外の「他者」の、やはり、1.6倍、なのである。
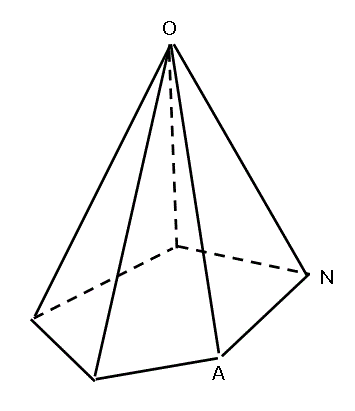
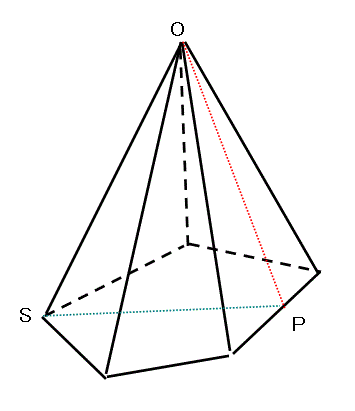
∠AON=θとし、正二十面体の場合と同様に
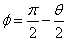 とおけば、
とおけば、
- △OANは、この正五角錐の側面であるから、
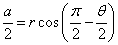 ・・・(1)
・・・(1)
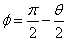 とおいたから、a=2rcosφ
とおいたから、a=2rcosφ
という条件は、何ら変わらない。 - 右図において、PSの長さが、この正五角形を真っ二つに断ち切る線分の長さ、に等しいこと、これが二つ目の条件になる。
この長さは、一辺aの正五角形の対角線の長さ、「黄金比」をkと書けば、ka、に、sin(2π/5)をかけたものになるだろう。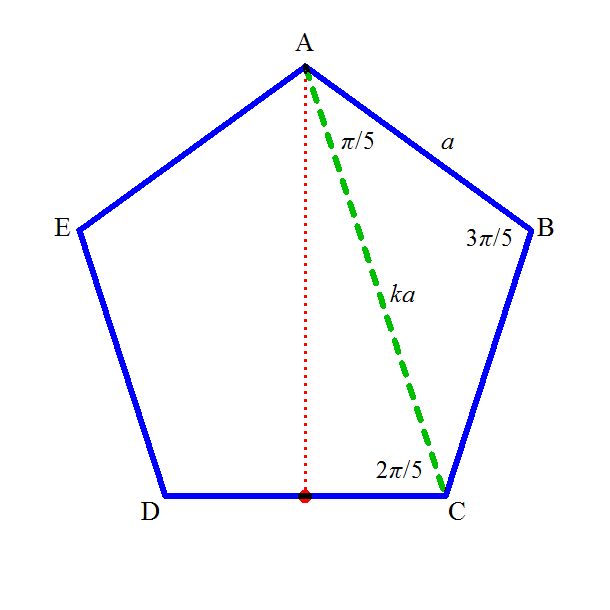
OPは、側面の二等辺三角形の頂角二等分線であるから、OP=rsinφ、∠POS=φであるから、「余弦定理」を用いて、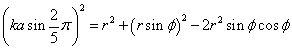 ・・・(2)
・・・(2)
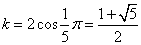 であるから、
であるから、
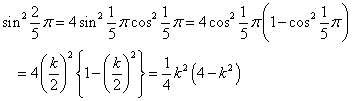
さらに、
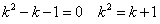 であったことを思い出せば、
であったことを思い出せば、
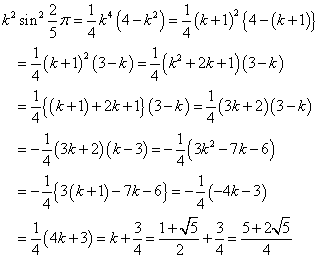
(1)、(2)から、
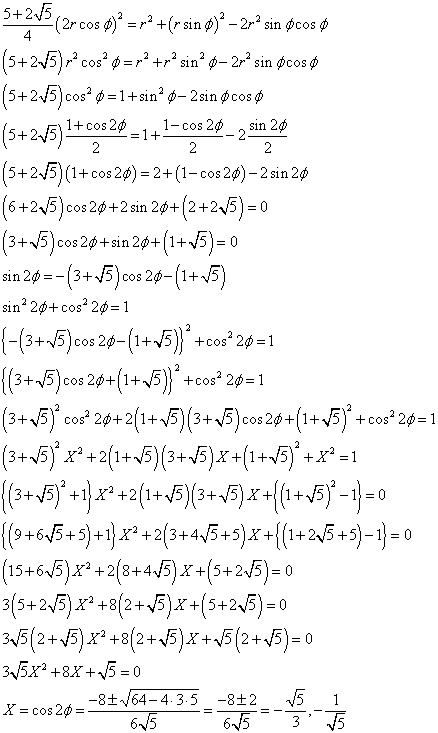
ここで、
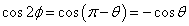 であるから、
であるから、
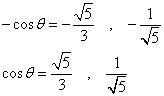
もう、全然計算合ってる気がしないが、意外に「エレガント」な(笑)数値になったから、続けてみた。二つでてきた解のうち、一方は、正二十面体のものと同じになっている。これはもちろん「解」から除外しなければならないのだが、その条件はなんなのか?
√5/3に対するθは、それぞれ41.8103149、妥当な値ではある。。
| 一点から発する線分の数 | 対応する正凸多面体 | 最も近い2線分のなす角の余弦 | 最も近い2線分のなす角 |
| 2 | (直線) | -1 | 180 |
| 3 | (正三角形) | -1/2 | 120 |
| 4 | 正四面体 | -1/3 | 109.4712206 |
| 6 | 正八面体 | 0 | 90 |
| 8 | 正六面体 | 1/3 | 70.52877937 |
| 12 | 正二十面体 | 1/√5 | 63.43494882 |
| 20 | 正十二面体 | √5/3 | 41.8103149 |
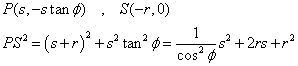
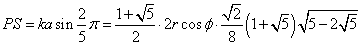
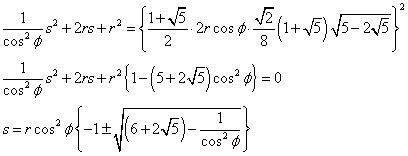
この凄まじい2次方程式に上の結果のφを代入して、解の複号はどうやらマイナスの方を採用しなければならないようで、その数値からグラフを描いた訳である。眺めてみると、結構「イケてる」ではないか?
「多面体に関するオイラーの公式」、に、話を戻す。面(faces)の数F、頂点(vertices)の数V、辺(edges)の数E、の間には、
F+V-E=2
が、成り立つ。正凸多面体であるならば、空間のどの方向にも「対等」に、広がっているのだから、その頂点や、辺の数を数えるのは、なかなか難しい。「ぐにゃぐにゃ」の、「位相幾何学的同型性を保った」変形を施して、平面に射影する、上から覗き込むようにして眺めるのだけれど、実際なら、「前傾」の背後に隠れた「後景」となってしまうものも、全部、重ならずに見えるように描く、と、正四面体、正六面体(立方体)、正八面体、正十二面体については、次の図のようになる。あと、正二十面体があるのだけれど、力尽きて(笑)やめたのだった。
| 正四面体 | 正六面体 | 正八面体 | 正十二面体 | |
| 見取り図(透視図) | 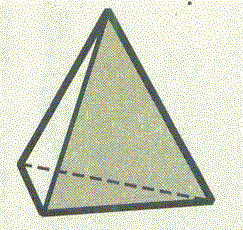 | 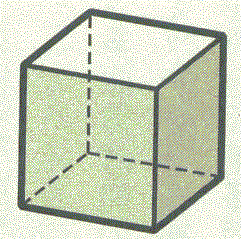 | 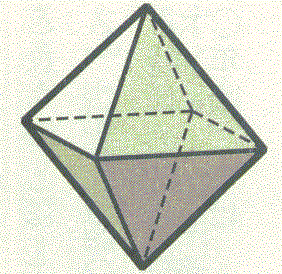 | 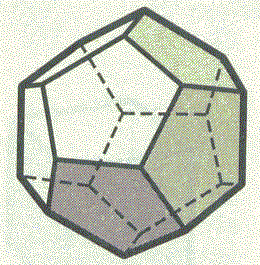 |
| 平面への射影 |  |  |  |  |
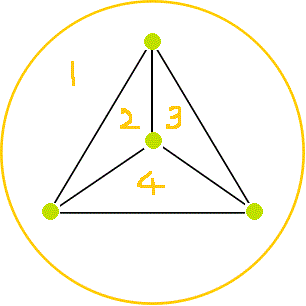
例えば正四面体について、上の図のように、オレンジ色の円で囲まれた「外」に「はみ出した」領域にも番号を振って数えれば、ちゃんとF=4、V=4、E=6、F+V-E=2が成り立っているではないか?、立体について考える「代わりに」、この平面上の「模様」について、考え、この「公式」の、「証明」の如きものができるではないか!
この「図」に対して、F+V-E=2なる「関係」が維持されるような「変形」を施し、順次単純化していく。これ以上単純化できないところまで行って、なお、この等式が成り立っているのならば、・・・、今度はこれを逆順に辿り、「数学的帰納法」としての「証明」として記述することができる。
辺を一本ずつ、取り外していこう。
 →
→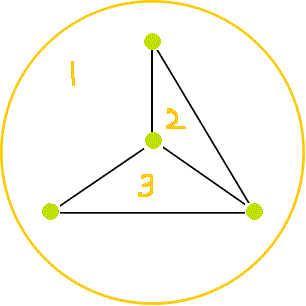 →
→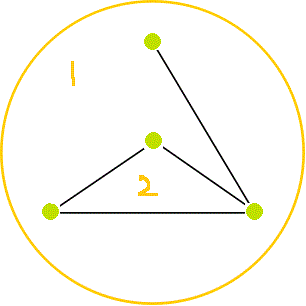 →
→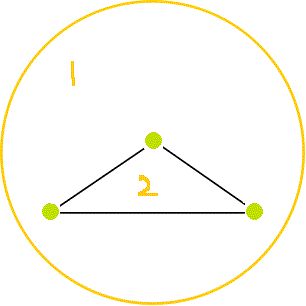 →
→ →
→ →
→
その一ステップごとの変形を、見ていくと、
 → → | Eがひとつ減り、 Fがひとつ減った。 Vは変わらない。 F=3,V=4,E=5 F+V=E=2 |
 → → | Eがひとつ減り、 Fがひとつ減った。 Vは変わらない。 F=2,V=4,E=4 F+V=E=2 |
 → → | Eがひとつ減り、 Vがひとつ減った。 Fは変わらない。 F=2,V=3,E=3 F+V=E=2 |
 → → | Eがひとつ減り、 Fがひとつ減った。 Vは変わらない。 F=1,V=3,E=2 F+V=E=2 |
 → → | Eがひとつ減り、 Vがひとつ減った。 Fは変わらない。 F=1,V=2,E=1 F+V=E=2 |
 → → | Eがひとつ減り、 Vがひとつ減った。 Fは変わらない。 F=1,V=1,E=0 F+V=E=2 |
地図の塗り分けに関する「四色問題」に関連して、重要な定理があるそうで、それは、
「どんな地図にも、5個以下の隣接領域しか持たない領域が、少なくともひとつ含まれる」
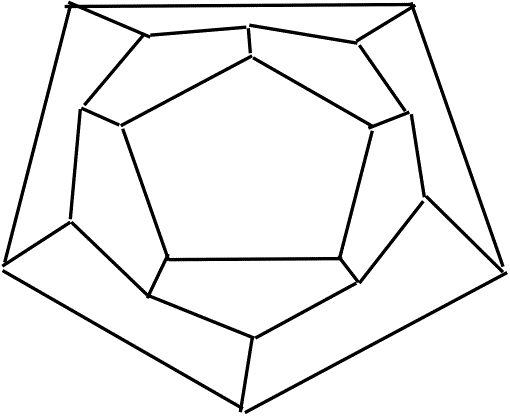
というものだ。例えば、先の正十二面体を「ぐにゃぐにゃに」潰した平面図を、「地図」だと看做せば、・・・、ただ一つ上から見ることのできない底面を、まわりに「はみ出した」オレンジ色の円、これも一つの領域、本物の地図なら、大陸や島を取り囲む「海」もまた、ひとつの「国」と同等な「領域」と看做せば、
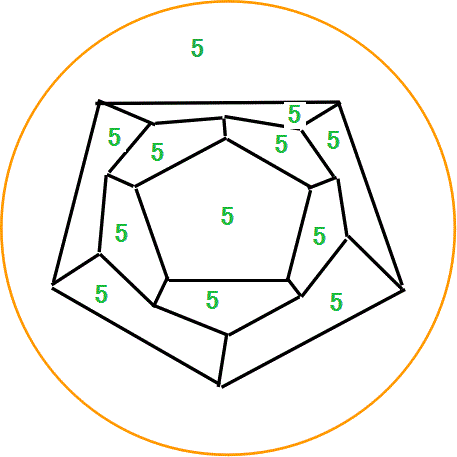
図中に付した数字は、その「領域」が隣接する「領域」の個数である。すべてが、「5」だから、もちろんこの地図は上の定理を満たしている。正十二面体の各面は正五角形なのだから当然といえば当然である。この定理の証明に、「多面体に関するオイラーの公式」が用いられる、という興味深い話があるので、持ち出した。その証明には、「背理法」が使われる。
命題p→qが成立するならば、条件p、qをみたす「もの」の集合をそれぞれ、P、Qとすれば、P⊂Q、PがQに包含されている、でなければならない。これは、P∩¬Q=φ、Pと「Qの補集合」との共通部分が空集合である、と同値だから、pかつ、qの否定、を仮定して矛盾を導けばよい、というロジックである。
「すべての領域が6個以上の隣接領域を持つような地図は、ありえない」
と、言いたいのである。
これは、正凸多面体を構成する正多角形が、正三角形、正方形、正五角形、でしかありえない、という理屈と、パラレルなのだと思う。多面体の頂点には少なくとも3つの面が合しているから、3つ加えて360°以上になっては困る。だから一つの内角が120°の正六角形をいくら並べても、いつまでたっても平面で、ちっとも立体にはなってはくれない。
上の「地図」を真似て、なるべく正六角形でできたものを描こうとしてみると、例えば下の図のようなもの、中央部の「蜂の巣」模様は、いくら増殖させても構わない、ただ、外側の最後の周縁部分が、五角形か四角形を混ぜなければ、「終わらない」、のである。
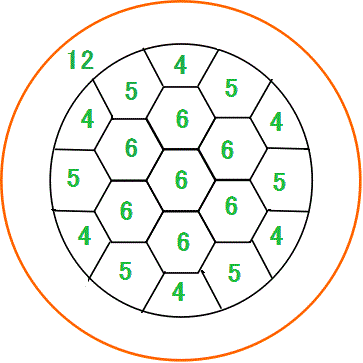
「すべての面が正六角形であるような正凸多面体は存在しない」、と、「すべての領域が6個の隣接領域を持つ地図は、描けない」、とは、同値なのだと思う。
では、証明に取り掛かろう。
「どんな地図にも、5個以下の隣接領域しか持たない領域が、少なくともひとつ含まれる」
を、示したいのであるから、
「すべての領域が、少なくとも6個の隣接領域を持つような地図が、存在する」と仮定して、矛盾を導くことになる。
そのような地図においては、
- ひとつの「頂点」には、少なくとも3本の境界線が出会う場所を「頂点」と呼ぶのだから当然にも、3本の辺(境界線)が対応する。
一方、一つの辺は、二つの頂点を結んでいるのだから、頂点数Vを3倍してしまうと、これはすべての辺を二回ずつ重複して数えたことになる。従って、
2E≧3V・・・(1) - 仮定から、すべての面は6個以上の隣接する面を持っている。つまりすべての面には6個以上の辺がある。
一方、一つの辺は、二つの面を隔てているのであるから、面の数Fを6倍してしまうと、これはすべての辺を二回ずつ重複して数えたことになる。従って、
2E≧6F・・・(2)
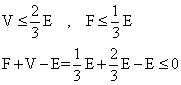
ほら、矛盾した!、証明終わり。
「多面体に関するオイラーの公式」の、もうひとつの応用例。もちろん、これも、「四色問題」ロビン・ウィルソン(新潮文庫)、による。
多面体についても、あるいは、それを「ぐにゃぐにゃに」潰して得られた「地図」に対しても適用できる、「数えあげの公式」なるものがあるそうで、その導出と、ちょっとした「応用」を以て、このネタもそろそろ飽きてきたし(笑)、終わりにしたい。もちろん、誰も続けろ、と言ってくれるわけでもないが(泣)。

正凸多面体であるならば、それを構成する面は、正三角形、正方形、正五角形、のいずれかであった。「面」である限り、少なくとも3直線で囲まれていなければならない。いくら「ぐにゃぐにゃに」変形しても、「どの領域も、3つ以上の境界線に囲まれている」という制限を持ち込まないと、「多面体」と「地図」の互換性が失われる。実際の「世界」には、二つの境界線のみで囲まれた「国」は、存在する。
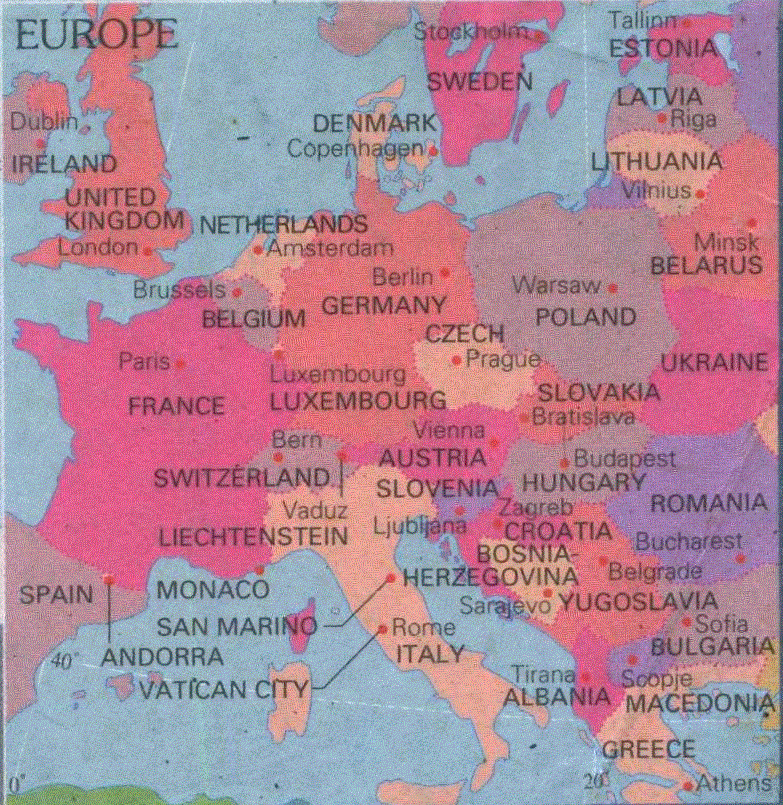
フランス、スペイン国境「上」に存在するアーンドラには、フランス・アーンドラ国境、スペイン・アーンドラ国境、の二種類の国境線しかない。それどころか、たった一種類の境界線しかもたない国さえある。バチカンは、ローマ市内にあり、四囲をすべてイタリアという「他国」に囲まれているのである。
もうひとつの制限は、多面体ならば、すべての「頂点」、・・・、「地図」の話なら、それは境界線の交わる交点、であるが、は、ことごとく「3枝頂点」で出来ていることにしたい。正凸多面体で言うならば、正八面体はすべて「4枝頂点」、正二十面体ならばすべて「5枝頂点」で出来ている。このようなものは除外しよう、というのである。「地図」の塗り分け、という数学上の関心からも、4枝以上を認めると、辺を共有しない限り同じ色で塗ってよいから、制限が緩和されて「面白みを欠く」ばかりでなく、現実の「地図」ならば、・・・、植民地主義者が、地図の上に定規を当てて決定した、下の左図のような国境が、存在する可能性をなしとはしないものの、・・・、4国の検問所がその交点に当たる場所に「軒を並べて」いる、というのはありそうもない話で、例えばA国からD国へ移動する際、B国またはC国の通行査証が求められるのなら、下の真中の図、どちらも不要なのなら、下の右図、・・・、というように、実際には、少しずれている、と考えて差し支えないのである。
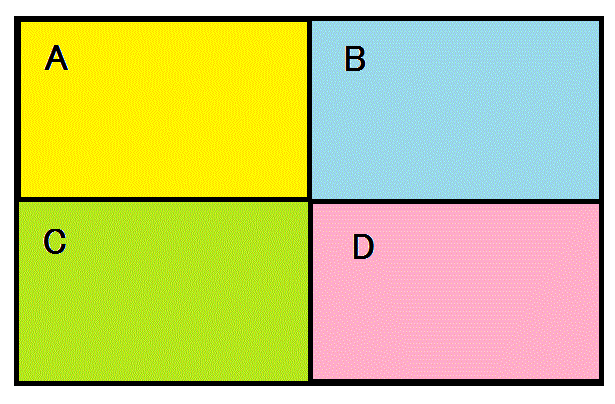
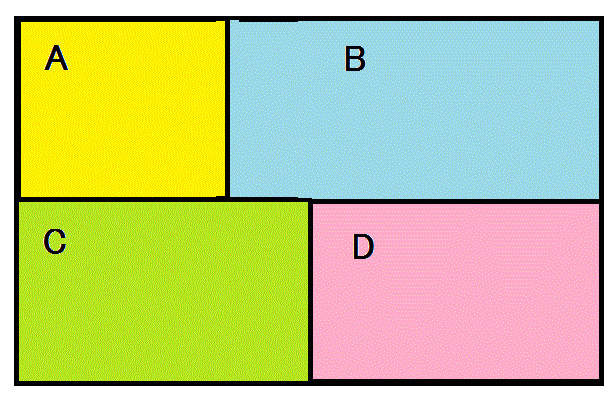
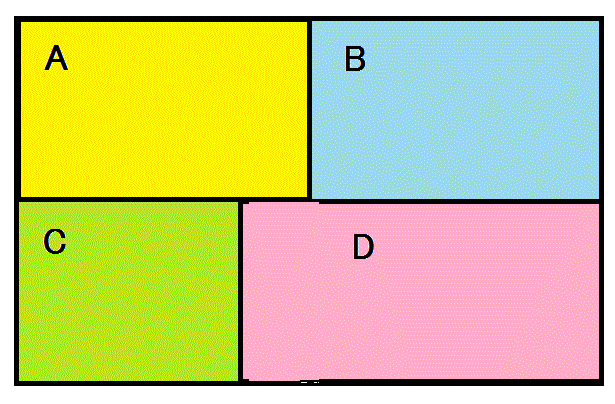
- すべての領域は、少なくとも3つの境界線に囲まれていること、
- すべての頂点(境界線の交点)では、ただ3本のみの境界線が出会っていること、
k本の境界線(辺)で囲まれた領域の個数を、Ckと呼ぶことにする。
「地図」上のすべての領域の個数、多面体ならば全ての面の個数は、これらの和であるから、面の数Fは、次のように表されるであろう。
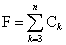
一方、辺の数Eについては、・・・、k個の隣接領域をもつ領域は、k個の境界線(辺)をもつだろう、ところがこれをすべて加算すると、境界線(辺)というものはそれぞれ二つずつの領域(面)の間に存在するものであることに鑑み、
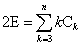
一つの頂点には、3本の境界線が会する。頂点数Vを3倍すれば、これは、境界線(辺)というものがそれぞれ二つの頂点を結ぶものであることに鑑み、辺の数Eの2倍と等しい。
3V=2E
よって、Vは、次のように書ける。
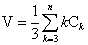
「多面体に関するオイラーの公式」によれば、F+V-E=2であった。
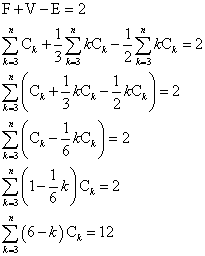
これが「数えあげの公式」である。今回は、ここまでにする。
では、「数えあげの公式」、k本の境界線(辺)で囲まれた領域の個数を、Ckとすると、
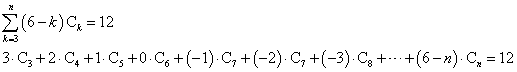
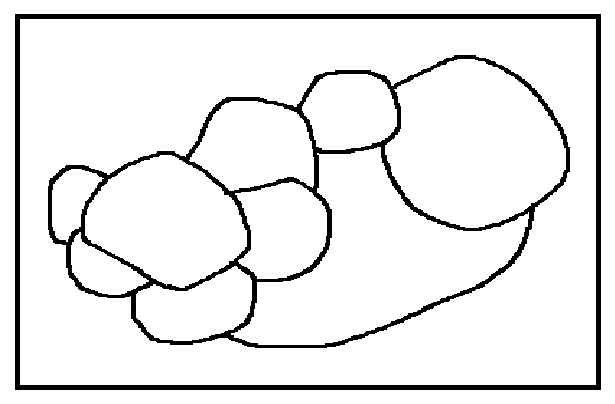
を、具体例で確かめてみたい。下の左図の如き「地図」があったとする。「多面体」としてなら、上から覗き込んで見えないただ一つの「底面」が「外」にはみ出したとした、この島状の「陸地」が浮かぶ「海」もまた、ひとつの「領域」と数えると、各領域にアルファベットの「名前」を付せば、下、右図のようになる。
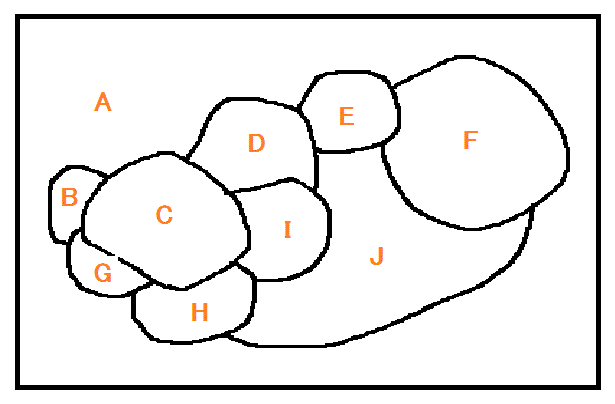
| 領域名 | 隣接する領域 | 隣接する領域の個数 |
| A | I以外すべて | 9 |
| B | A,C,G | 3 |
| C | A,D,I,H,G,B | 6 |
| D | A,E,J,I,C | 5 |
| E | A,F,J,D | 4 |
| F | A,J,E | 3 |
| G | A,B,C,H | 4 |
| H | A,G,C,I,J | 5 |
| I | C,D,J,H | 4 |
| J | A,H,I,D,E,F | 5 |
C3=2,C4=3,C5=3,C6=1,C7=0,C8=0,C9=1
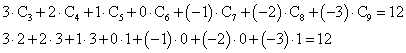
なるほど(笑)、あっている!
こうなってくると、こんな、変な、わざとらしい作り物の地図ではなく、もう少し複雑な、「本物の」(笑)地図で、試してみたくなるのが、人情であろう。
私が、当地、沖縄にやってきたのは15年前、その時「も」失業していて(笑)、その時「も」、「人生」に「絶望」していた(笑)。「失業保険」、正確に言うと、「雇用保険の失業者給付」はもちろん、失業者の真剣な求職活動を援助するのが制度趣旨であるから、給付を受けながら「旅行」など論外なのであるが、「人生」に「絶望」していた私は(笑)、部屋に篭って一日をパソコンのカードゲームに費やす、わ、今と同じだ!、ぐらいなら、いっそ、「そうだ、旅に出よう!」と、決心したのだった。職業安定所に出頭しなければならないインターバルが、一ヶ月、さて、「北」に向かうか「南」に向かうか?、Tシャツと短パン、ゴム草履で歩いていても怪しまれない(笑)「南」の方が、お金がかからなさそう、と踏んだ、・・・、それが私とこの島の「縁」を取り結んだのである(笑)。
大阪南港から、那覇、宮古、石垣を経て、はるか台湾の基隆であったか高雄であったか、を最終目的地とするフェリー、今はその会社は倒産してしまったが、は、バックパッカー的貧乏旅行者の定番で、「降るように星が見えますよ!」、と教えてくれる人もいた。
残念なことに、私の場合、全行程、曇りで、デッキに出てもつまらないから、もっぱら自動販売機の「オリオンビール」を啜りながら、京都の書店で買い求めた沖縄県道路地図、を眺めていたのである。
おかけで、市町村名、国道の番号と起点、終点、・・・、それから、ほとんどどのページにも、巨大な「空白」として残されている米軍基地の位置と名前も、すべて「暗記」することができた。
その後、いくつかの市町村合併があったのだけれど、この地図にはそんな「懐かしさ」があるし、また、細かく複雑な方が、ここでの「問題」としてはふさわしいので、これを採用する。
当時沖縄本島には、33の市町村があった。本当は、本部町の沖合、ほんの目と鼻の先(笑)に、伊江村を構成する伊江島が浮かんでいるのだが、これは、前回述べたように、「海」というただ一つの領域に囲まれた領域であるから、ルール違反、ということで、除外した。
33の市町村及び「海」、の合計34個の領域について、その隣接領域の個数を調べ、「数え上げ公式」に適用してみる。ひまにまかせて何度やってみても、しかし、合わないのである。小一時間ばかり経ってやっと気づいたのは、
- 名護市の境界線をぐるりとなぞってみよう。「海」が、断続的に、3回、現れるのである。
- 同様に、具志川市、「海」と、2回、隣接している。
なにか補助的な証明が必要なのであろうが、それは私の手に余るから(泣)、やや座りは悪いけれど、ともかく、名護市に関して「海」を3回、具志川市に関して「海」2回、そして、「海」に関して、名護市3回、具志川市2回数えると、なんと、う・ま・く・い・く・、のであった。
物を数えるには、「ルール」を定めなければならない。数学の常道に従って、x軸正方向から「反時計回りcounter-clockwise」で行くことにする。その順番に、各「領域」の境界をなぞってみて、出会った隣接領域を列挙する。
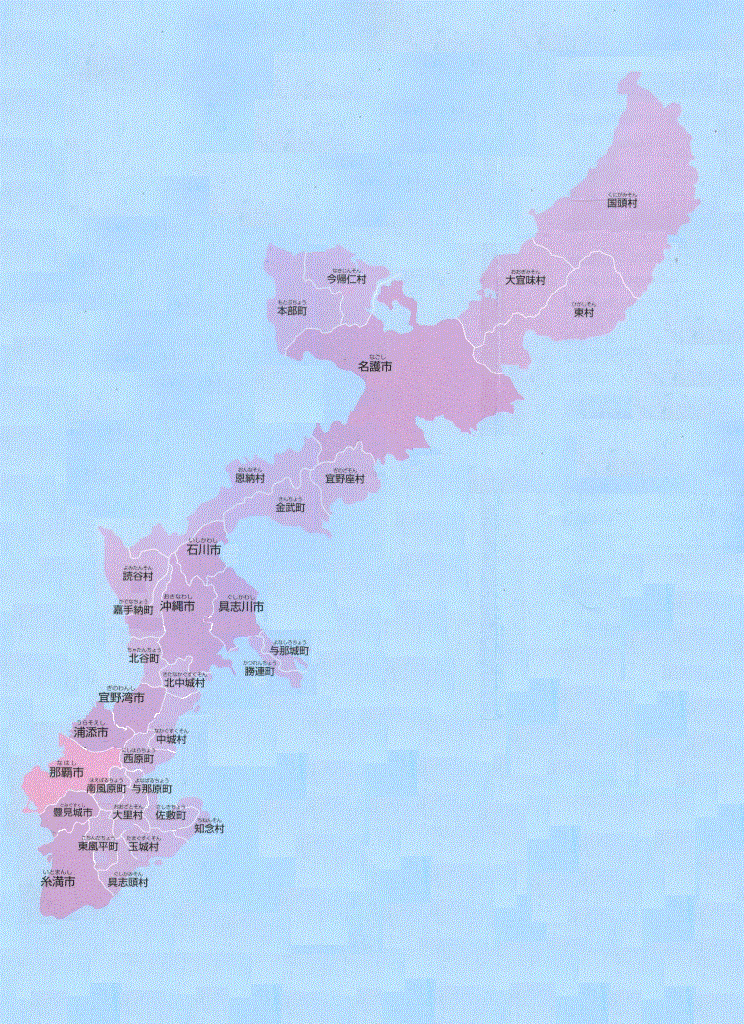
| 番号 | 市町村 | 隣接する市町村、及び、海 | その個数 |
| 1 | 国頭村 | 海、大宜味村、東村 | 3 |
| 2 | 大宜味村 | 東村、国頭村、海、名護市 | 4 |
| 3 | 東村 | 海、国頭村、大宜味村、名護市 | 4 |
| 4 | 名護市 | 東村、大宜味村、海(1)、今帰仁村、本部町、海(2)、恩納村、宜野座村、海(3) | 9 |
| 5 | 今帰仁村 | 海、本部町、名護市 | 3 |
| 6 | 本部町 | 今帰仁村、海、名護市 | 3 |
| 7 | 恩納村 | 宜野座村、名護市、海、読谷村、沖縄市、石川市、金武町 | 7 |
| 8 | 宜野座村 | 海、名護市、恩納村、金武町 | 4 |
| 9 | 金武町 | 宜野座村、恩納村、石川市、海 | 4 |
| 10 | 石川市 | 海、金武町、恩納村、沖縄市、具志川市 | 5 |
| 11 | 読谷村 | 嘉手納町、沖縄市、恩納村、海 | 4 |
| 12 | 沖縄市 | 具志川市、石川市、恩納村、読谷村、嘉手納町、北谷町、北中城村、海 | 8 |
| 13 | 具志川市 | 海(1)、石川市、沖縄市、海(2)、勝連町、与那城町 | 6 |
| 14 | 与那城町 | 海、具志川市、勝連町 | 3 |
| 15 | 勝連町 | 与那城町、具志川市、海 | 3 |
| 16 | 嘉手納町 | 沖縄市、読谷村、海、北谷町 | 4 |
| 17 | 北谷町 | 北中城村、沖縄市、嘉手納町、海、宜野湾市 | 5 |
| 18 | 北中城村 | 海、沖縄市、北谷町、宜野湾市、中城村 | 5 |
| 19 | 宜野湾市 | 中城村、北中城村、北谷町、海、浦添市、西原町 | 6 |
| 20 | 中城村 | 海、北中城村、宜野湾市、西原町 | 4 |
| 21 | 浦添市 | 西原町、宜野湾市、海、那覇市 | 4 |
| 22 | 西原町 | 海、中城村、宜野湾市、浦添市、那覇市、南風原町、与那原町 | 7 |
| 23 | 那覇市 | 南風原町、西原町、浦添市、海、豊見城市 | 5 |
| 24 | 南風原町 | 与那原町、西原町、那覇市、豊見城市、東風平町、大里村 | 6 |
| 25 | 与那原町 | 海、西原町、南風原町、大里村、佐敷町 | 5 |
| 26 | 豊見城市 | 東風平町、南風原町、那覇市、海、糸満市 | 5 |
| 27 | 東風平町 | 具志頭村、大里村、南風原町、豊見城市、糸満市 | 5 |
| 28 | 大里村 | 佐敷町、与那原町、南風原町、東風平町、具志頭村、玉城村 | 6 |
| 29 | 佐敷町 | 知念村、海、与那原町、大里村、玉城村 | 5 |
| 30 | 知念村 | 海、佐敷町、玉城村 | 3 |
| 31 | 糸満市 | 東風平町、豊見城市、海、具志頭村 | 4 |
| 32 | 具志頭村 | 海、玉城村、大里村、東風平町、糸満市 | 5 |
| 33 | 玉城村 | 海、知念村、佐敷町、大里村、具志頭村 | 5 |
| 34 | 「海」 | 30市町村プラス名護市(2)、具志川市(1) | 33 |
| 隣接する領域の個数 | その領域の個数 | |
| C3 | 3 | 6 |
| C4 | 4 | 9 |
| C5 | 5 | 10 |
| C6 | 6 | 4 |
| C7 | 7 | 2 |
| C8 | 8 | 1 |
| C9 | 9 | 1 |
| ・・・ | ||
| C33 | 33 | 1 |
| 計 | 34 |