下図のような遊園地のジェットコースターについて考える。
高さH mのA地点から、初速度0 m/sですべり降り、中央部の半径R mの円軌道を通過する。
|
レールとジェットコースターとの間には摩擦はまったくないと仮定しよう。また、実際の遊園地ではジェットコースターはレールから決して離れないように安全設計されているであろうが、ここでは、ジェットコースターがレールから受ける垂直効力を失うと軌道から外れて落下してしまう、と仮定する。 また、中央部の円は実際は一番下のB地点で少しずれなければ通れないから、完全な円軌道ではないのだが、これも無視し、ジェットコースターが進行方向に対して左右方向に軌道をずれて脱落することもないとする。 |
- 最下点Dから反時計回りにθ進んだ点Pにおけるジェットコースターの速さvを求めよ。
A点とP点におけるエネルギー保存則から、
 ・・・(1)
・・・(1)
したがって、
v=
- P点においてジェットコースターが軌道から受ける垂直抗力Nを求めよ。
法線方向についてだけ、運動方程式を立てる。
 ・・・(2)
・・・(2)
(1)(2)からvを消去して、
N=
- ジェットコースターが軌道から外れることなく円軌道を通過できるために、HとRが満たすべき関係を求めよ。
0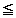 θ
θ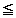 2π の範囲では、N は θ= ( ) のとき最小値をとる。このとき、N
2π の範囲では、N は θ= ( ) のとき最小値をとる。このとき、N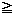 0であればよいから、
0であればよいから、

したがって、求める条件は、 H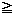
 R
R
|
|
水平面上に、これと角度θをなす斜面を持つ質量 M kg の台が置かれている。水平面から高さ h m の斜面上(A点)に質量 m kg の小物体を置き、静かに手を放す。
この後の小物体および台の運動について考える。水平面と台との間に摩擦はなく、小物体と斜面との間の動摩擦係数を μ' とする。
水平面上にいる観測者からみた台の加速度の大きさをb[m/s2]、
台上にいる観測者からみた小物体の(相対)加速度の大きさをa[m/s2]として、
- 水平面上にいる観測者から見た、台の運動について
- 鉛直方向「つりあいの式」
 ・・・(1)
・・・(1)
- 水平方向「運動方程式」
 ・・・(2)
・・・(2)
- 鉛直方向「つりあいの式」
- 台上の観測者からみた、小物体の運動について
- 斜面に垂直な方向「つりあいの式」
 ・・・(3)
・・・(3)
- 斜面に平行な方向「運動方程式」
 ・・・(4)
・・・(4)
- 斜面に垂直な方向「つりあいの式」
- 台と小物体の間に作用する動摩擦力について
 ・・・(5)
・・・(5)
水平面上にいる観測者から見た、台の運動について考える。
| |
|
水平面上にいる観測者からみた、小物体の運動を考えようとしても、加速度の方向がわからない。 そこで観測者を台上に移し、「慣性力」をもち込む。 | |
|
台上の観測者からみた、小物体の運動。
|
以上5式から、5個の未知数N1 , N2 , f , a , bについて、解けばよい。参考までに、・・・
(2),(5)からfを消去、これと(3)からbを消去する。
こうして、N1が求められる。
(5)より、
(2)より、
(4)に代入して、
最後に、(1)から、
水平面と角度θをなす斜面上に、自然長 l0 m、ばね定数 k のばねが、図のように固定されているとする。
斜面に沿って下向きにx軸をとり、ばねが固定されている点を原点とする。
x = l 地点で手を放した瞬間を t = 0 として、 おもりの位置 x を t の関数として表現したい。
ただし、おもりと斜面との間には摩擦はないものとする。
つりあいの位置は、 x =

振幅は、
 [m]
[m]
周期は、
 [s]
[s]
おもりの位置 x を t の関数としてあらわすと、
x =

|
|
|
|
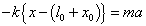 ・・・(2)
・・・(2)
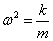
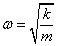 [(rad)/s]
[(rad)/s]
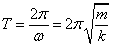 [s]
[s]
 U [J] と、絶対温度の変化量
U [J] と、絶対温度の変化量  0
0
 T2
T2