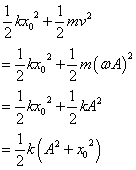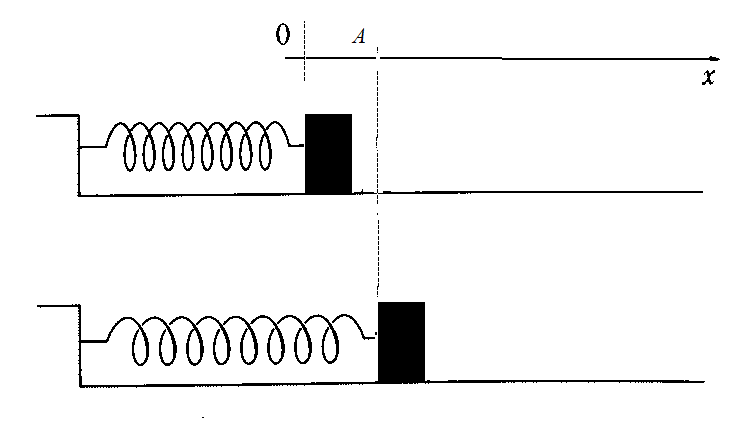
バネ定数kのバネを水平に置き、一端を固定して他端に質量mのおもりをつける。
ばねの延びる方向にx軸をとり、自然長をx=0とする。
時刻t=0に、x=Aまでバネを引っ張り、手を離す。
- 運動方程式:-kx=ma
初期条件:t=0で、x=A - x=Acosωt
v=-ωAsinωt
a=-ω2Acosωt=-ω2x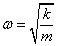
| 重力による 位置エネルギー | 弾性力による 位置エネルギー | 運動エネルギー | 合計 | ||
| 変位x | - |  kA2cos2ωt kA2cos2ωt |  m(-ωAsinωt)2 m(-ωAsinωt)2=  kA2sin2ωt kA2sin2ωt |  kA2 kA2 | |
| x=A | - |  kA2 kA2 | 0 |  kA2 kA2 | |
| x=0 | - | 0 |  mω2A2= mω2A2= kA2 kA2 |  kA2 kA2 |
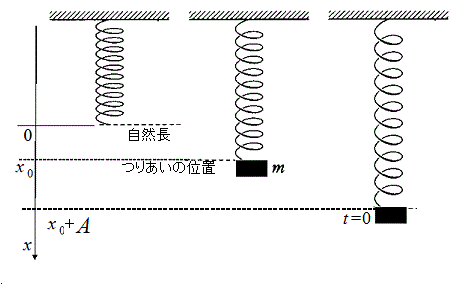
バネ定数kのバネを天井からつり下げ、下端に質量mのおもりをつける。
鉛直下方にx軸をとり、自然長をx=0とする。
つりあいの位置をx=x0とする。
時刻t=0に、つりあいの位置からさらにA、すなわちx=x0+Aまでバネを引っ張り、手を離す。
- 単振動を行わせる前の、つりあいの式:-kx0+mg=0
すなわち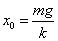
- 単振動をはじめたあとの、運動方程式:-kx+mg=ma
初期条件:t=0で、x=x0+A - 運動方程式を変形して、
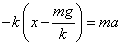
すなわち -k(x-x0)=ma
X=x-x0 と置き換えると、 -kX=ma
したがって、X=Acosωt すなわち、x=Acosωt+x0 - x=Acosωt+x0
v=-ωAsinωt
a=-ω2Acosωt=-ω2(x-x0)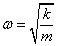
重力による位置エネルギーの基準面を、x=0(自然長)として、エネルギー保存則を考えると、
| 重力による 位置エネルギー | 弾性力による 位置エネルギー | 運動エネルギー | 合計 | ||
| 変位x (*1) | -mgx =-mg(Acosωt+x0) |  kx2 kx2=  k(Acosωt+x0)2 k(Acosωt+x0)2 |  m(-ωAsinωt)2 m(-ωAsinωt)2=  kA2sin2ωt kA2sin2ωt |  k(A2-x02) k(A2-x02) | |
| x=x0+A (*2) | -mg(x0+A) |  k(x0+A)2 k(x0+A)2 | 0 |  k(A2-x02) k(A2-x02) | |
| x=x0 (*3) | -mgx0 |  kx02 kx02 |  mω2A2= mω2A2= kA2 kA2 |  k(A2-x02) k(A2-x02) |
- (*1)の計算経過
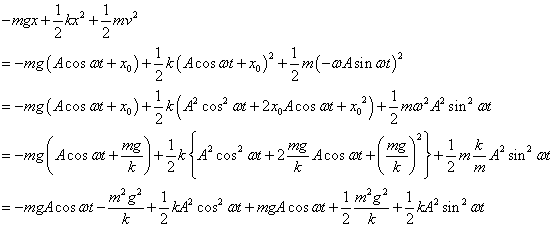
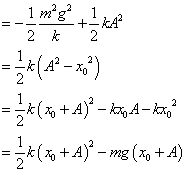
- (*2)の計算経過
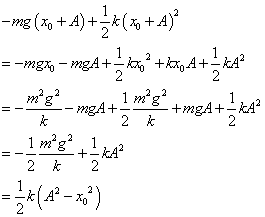
- (*3)の計算経過
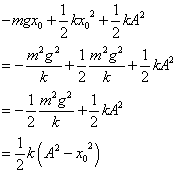
重力による位置エネルギーの基準面を、x=x0(つりあいの位置)として、エネルギー保存則を考えると、
| 重力による 位置エネルギー | 弾性力による 位置エネルギー | 運動エネルギー | 合計 | ||
| 変位x (*1') | -mg(x-x0) =-mgAcosωt |  kx2 kx2=  k(Acosωt-x0)2 k(Acosωt-x0)2 |  m(-ωAsinωt)2 m(-ωAsinωt)2=  kA2sin2ωt kA2sin2ωt |  k(A2+x02) k(A2+x02) | |
| x=x0+A (*2') | -mgA |  k(x0+A)2 k(x0+A)2 | 0 |  k(A2+x02) k(A2+x02) | |
| x=x0 (*3') | 0 |  kx02 kx02 |  mω2A2= mω2A2= kA2 kA2 |  k(A2+x02) k(A2+x02) |
- (*1')の計算経過
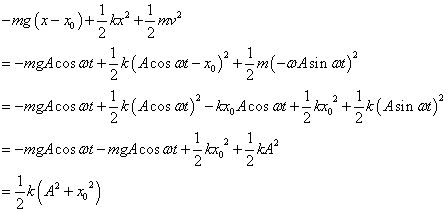
- (*2')の計算経過
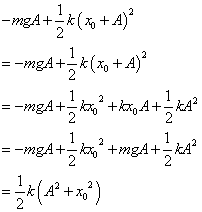
- (*3')の計算経過