• 時刻t=0に、導体棒PQを速度v₀で右(x軸正の方向)に動かす。
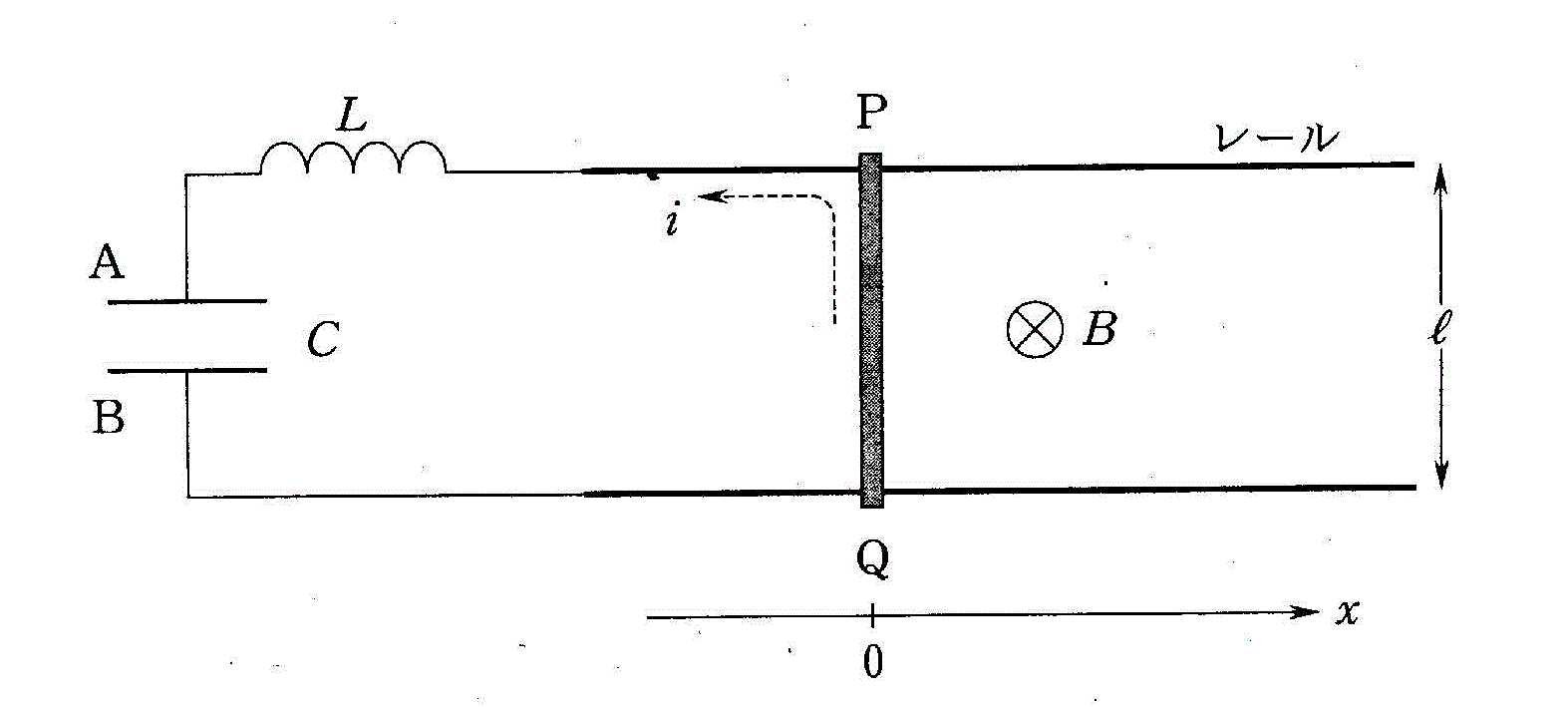
  回路に生じる誘導起電力の大きさは、
  
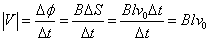
  その方向は、
  • 紙面を上から下に貫く磁場の増大という｢変化｣を｢打ち消す｣、すなわち、
  • 紙面を下から上に貫く磁場を生成する電流、すなわち、
    P→L→C→Q
    すなわち、PはQより高電位である。
• その電流の方向を正として、回路P→L→C→Qについてキルヒホッフ第二法則の式を立てる。
  • コイルに生じる自己誘導起電力は、電流iを妨げる方向だから、左側より右側が高電位、
  • コンデンサの極板Aには電流iが流入するから、正電荷がたまり、BよりAが高電位、
  であるから、極板Aの電荷を+qとすると、
  
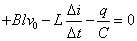
  ここで、極板Aには電流iが流入することから、
  
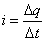
  したがって、
  
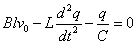
  これは、時間の関数q(t)の2階微分はqの1次関数であらわされることを意味している。
  定数項が消去されるように、変数変換を行うと、
  
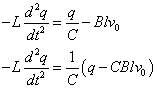
  q'=q-CBlv₀とおくと、d²q'/dt²=d²q/dt²だから、
  
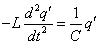
  この微分方程式の一般解は、
  
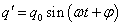
  ただしωは、
  
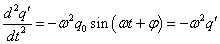
  より、
  
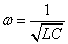
  次に、q₀および、ψは初期条件によって決まる積分定数である。
  • 時刻t=0において、q=0、すなわち、q'=-CBlv₀
  • 時刻t=0において、i=dq/dt=0、すなわち、dq'/dt=0、すなわち、q'が極値をとっていた、
  ことから、q'のグラフは｢-cos型｣であることがわかる。すなわち、
  
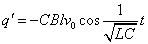
  qに戻すと、
  
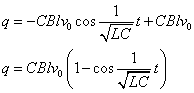
  電流iは、
  
• ところで、導体棒PQを流れるこの電流には、磁場から力を受けることになる。フレミング左手の法則から、
  
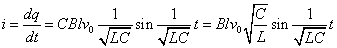
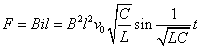
  その方向は、iの正の向き(Q→P)に対して左向き(x軸負の向き)である。
  このような振動する力を受ける導体棒に対して、右向き(x軸正の向き)に等速直線運動をさせるためには、これとちょうどつりあう外力を加え続けなければならない。
  したがって、この外力も、
  
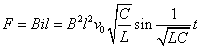
  とあらわされる。
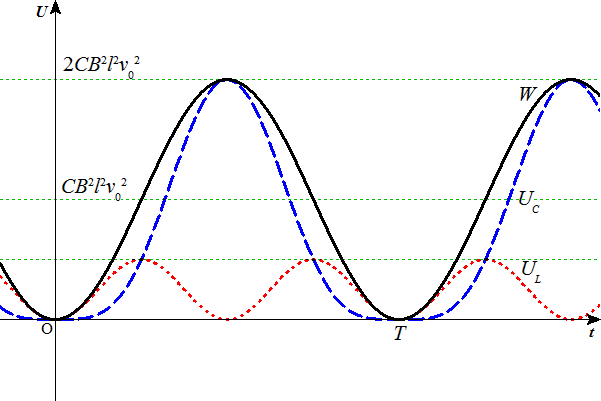
  この外力がする仕事は、
  
  
  
  
  
  
  
• 回路のエネルギー収支について考える。
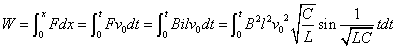
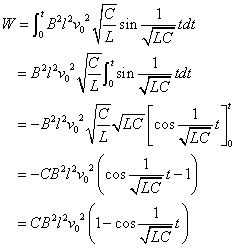
  コンデンサの蓄える静電エネルギーU_Cは、
  
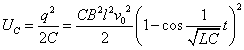
  コイルの蓄えるエネルギーU_Lは、
  
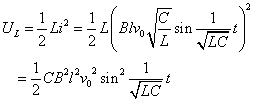
  これらの合計は、
  
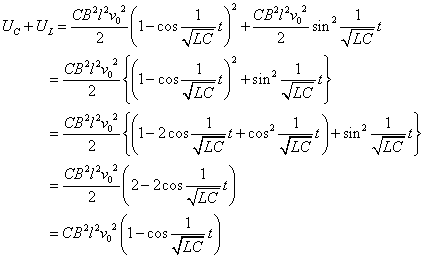
  したがって、 W=U_C+U_L である。