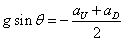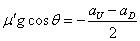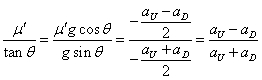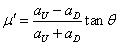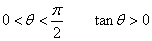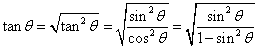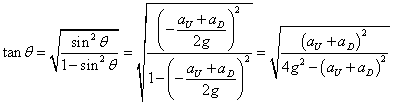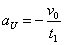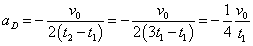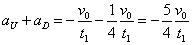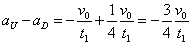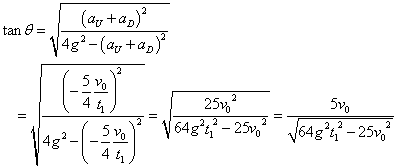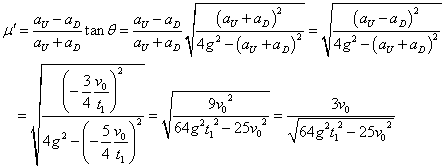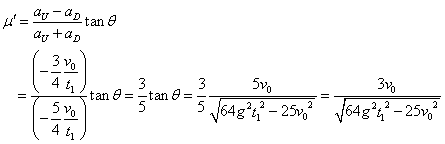粗い斜面の下端Oから小物体を速さv0で打ち出したところ、小物体は斜面上の点Pまで達し、その後下端Oに戻ってきた。
小物体が打ち出された時刻をt=0、点Pに達した時刻をt=t1とする。
また、小物体が下端Oに戻ってきたとき、小物体の速さは v0であった。
v0であった。
このとき、以下の値を、v0、t1、および重力加速度gを用いてあらわせ。
- 下端Oから点Pまでの距離L
- 小物体が下端Oに戻る時刻t2
- 斜面が水平面となす角をθとするときtanθ、ただし、0
 θ
θ
 π
π
- 斜面の動摩擦係数μ'
- Oを原点として、斜面に沿って上向きにx軸をとる。
v-tグラフは、
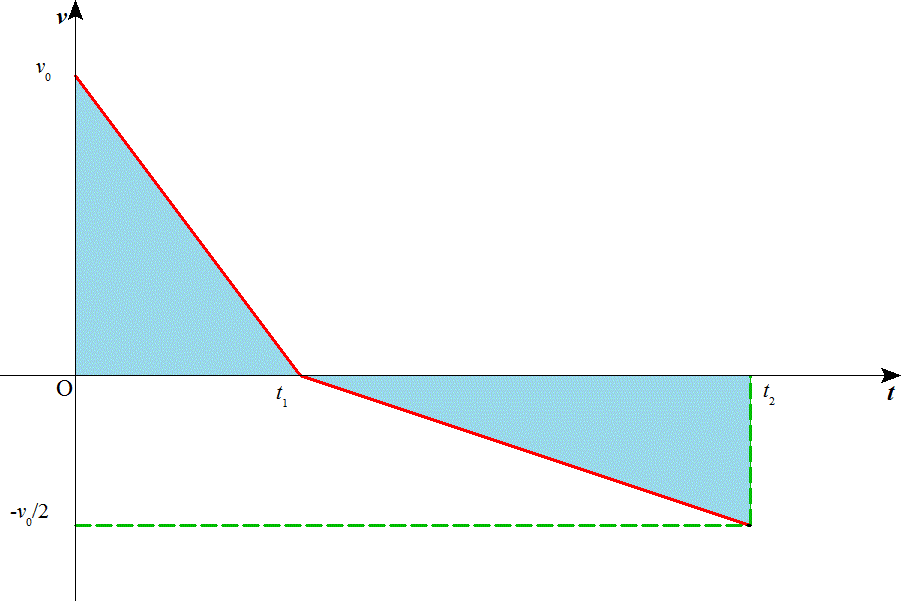
- v-tグラフの接線の傾きが、加速度aをあらわすから、
- aU:斜面を上昇するときの加速度
- aD:斜面を下降するときの加速度
とすると、
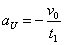 ・・・(1)
・・・(1)
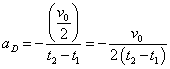 ・・・(2)
・・・(2)
- また、v-tグラフの曲線下の面積が、移動距離を表すから、
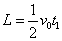 ・・・(3)
・・・(3)
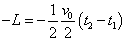 ・・・(4)
・・・(4)
- よって、iの答えは、
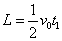
- (3)(4)より、
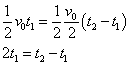
よって、
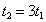
- Oを原点として、斜面に沿って上向きにx軸をとり、
M:小物体の質量
とすると、
- 運動方程式は、
- 上昇時:
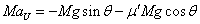
- 下降時:
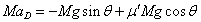
すなわち、
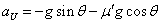 ・・・(5)
・・・(5)
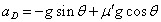 ・・・(6)
・・・(6)
(5)+(6) 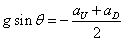
(5)-(6) 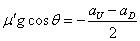
- したがって、
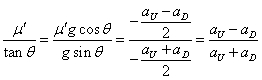
すなわち、
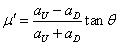
- また、
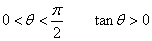
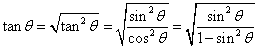
であるから、
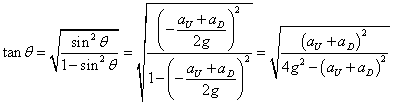
- ここで、
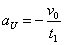
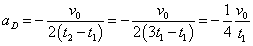
すなわち、
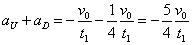
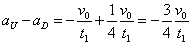
であるから、
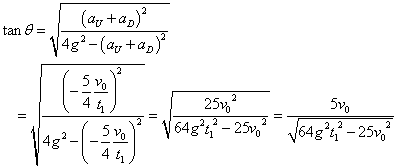
- さらに、
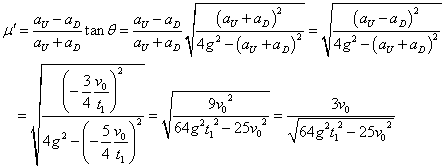
または、
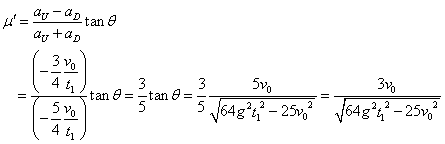
 θ
θ
 π
π
 v0であった。
v0であった。
 θ
θ
 π
π

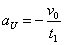 ・・・(1)
・・・(1)
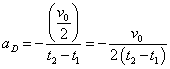 ・・・(2)
・・・(2)
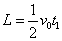 ・・・(3)
・・・(3)
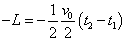 ・・・(4)
・・・(4)
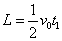
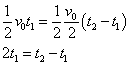
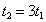
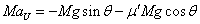
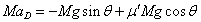
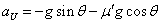 ・・・(5)
・・・(5)
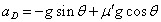 ・・・(6)
・・・(6)