• エネルギー保存則
  

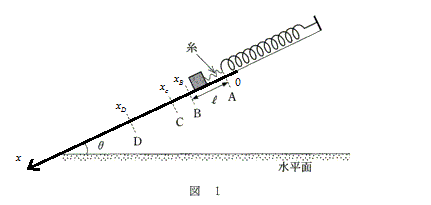
  	PG(重力による位置エネルギー)	PE(弾性力による位置エネルギー)	K(運動エネルギー)
  A	0	0	0
  B		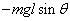0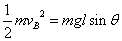
  C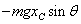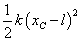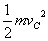
  D		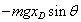	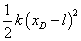0

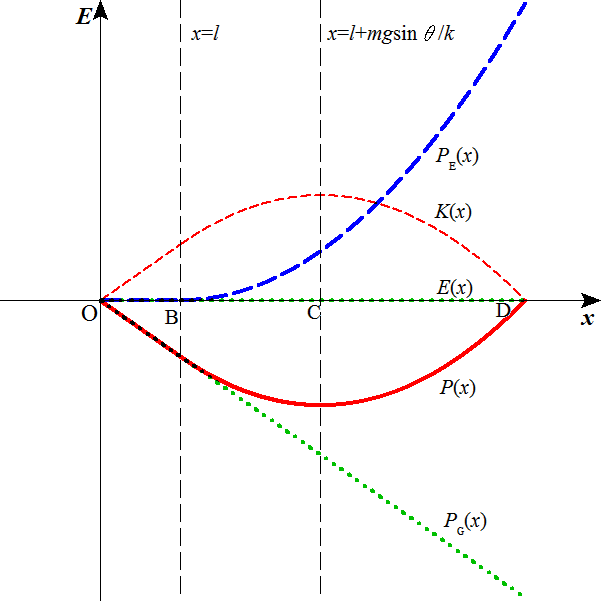
• 位置x ( ただし、xl ) におけるP_G(重力による位置エネルギー)とP_E(弾性力による位置エネルギー)の和を、P(x)とおくと、すなわち、
  P(x)=P_G+P_E
  とすると、
  
  
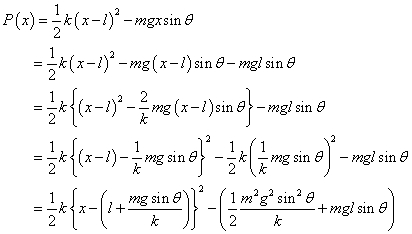
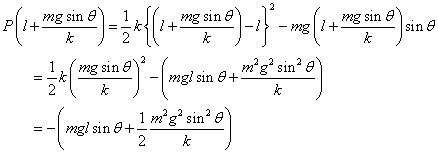
  または、
  
  
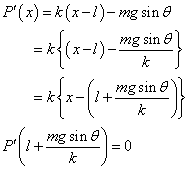
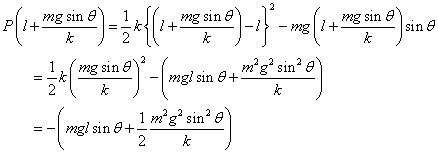
  となり、P(x)は、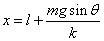で、極小値（最小値）をとることがわかる。
• 位置xにおける全エネルギーE(x)は、
  E(x)=P(x)+K(x)
  であるから、運動エネルギーK(x)が最大となるのは、P(x)が最小となるとき、
  すなわち、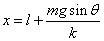である。
  速度vの大きさが最大となるのが、C点であるから、
  
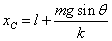
  ところで、｢つりあいの位置｣を、x=x₀とすれば、
  
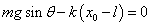
  すなわち、
  
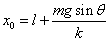
  であるから、x₀=x_C、C点は｢つりあいの位置｣であることがわかった。
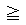• x_Dを求めたい。P(x)=0 ( ただし、xl ) となるxを求めればよい。
  
  
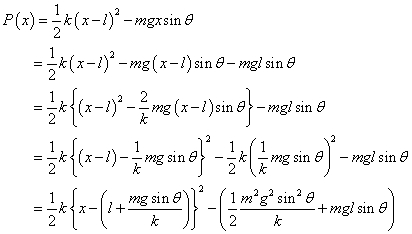
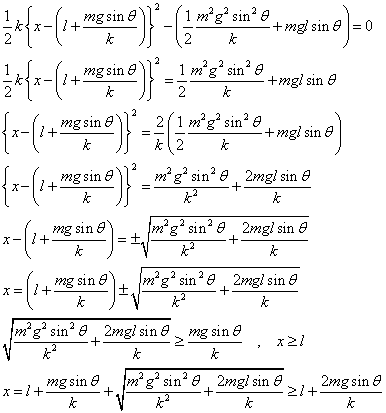
  となり、CD間の距離は、BC間の距離より少し長いことがわかる。
  これは、自然長Bの時点ですでに、運動エネルギーK= 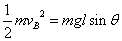をもっていたからで、
  BとDは、｢つりあいの位置｣Cに関して、｢対称｣とはならないのである。
• 横軸に距離をとって、各エネルギーのグラフを描くと、