- 速度v1[m/s]の電子を、長さl[m]の一様電場E[N/C=V/m]に、電場ベクトル(電気力線)に垂直な方向から進入させる。電子は電場からの一定の力により進路を曲げられ、放物運動を行うだろう。その進路のずれはわずかだが、これを電場のない空間を直進させることで拡大し、十分に離れたスクリーン上で検出することができる。
電子の進入速度v1[m/s]がわかっていれば、ここから、電子の比電荷(電子の持つ電荷[C]の、質量[m]に対する比)を算出することができる。
まず、ここまでを確認しよう。電子の質量をm[kg]、電荷を-e[C]とする。
- 電子の進行方向をx軸の正の向き、一様電場の向きをy軸の負の向きとする。
- 電場に進入した電子は、電場からy軸の正の向きにeE[N]の力を受ける。電子の質量は十分小さく、重力は、ここで問題にしている力に比べ無視できるとする。運動方程式
eE=ma
より、電子はy軸方向には、等加速直線運動を行う。
x軸方向には、なんらの力も作用していないから、初速度v1[m/s]で等速直線運動を行う。
vx=v1
x=v1t - 長さl[m]の一様電場を抜け出るまでに生じたy方向の進路のずれは、上の式でx=lのときのyを計算すればよい。これをy0[m]とすると、
一様電場の長さl[m]のちょうど中央から計って長さL[m]の場所にあるスクリーン上で検出される進路のずれy1[m]は、電子が一様電場を脱出するときの進行方向がx軸となす角をθとすれば、 - 一方、tanθは電子が一様電場を脱出するときのvyとvxの比であるから、
- 以上をまとめると、
- こうして、比電荷e/mは、
[(C/kg)={m・(m/s)2}/{(N/C)・m2}={m・(m/s)2}/{(kg・m/s2・C)・m2}]
となる。
右辺の各変数のうち、E,l,Lは実験装置の設計によって決定でき、y1は観測結果から得られる。したがって、電子が電場に進入する速度v1さえ明らかになったら、「比電荷」の算出が可能になることになる。19世紀末から20世紀初頭にかけて活躍したJ.J.トムソンが、どのようにして既知の速度の電子を発生させることができたのであろうか?
ここから先が、一様磁場における電子の等速円運動の問題である。
-
紙面の裏から表へ向かう方向に一様な磁場B[T=wb/m2]がある「箱」を考えよう。この箱の側面には
2r[m]の距離を隔てて二つの「穴」があけられている。一方の穴、「入口」からは、さまざまな速度をもった電子が、箱の壁面に垂直に進入する。箱に進入した電子は、磁場から「ローレンツ力」を受け、その持っていた速度に応じたさまざまな半径の等速円運動を行うだろう。
これらの電子のうち、半径r[m]の等速円運動を行うような速度をもった電子のみが、「出口」の穴から箱の外に出ることができる。
こうして、一様な磁場Bの大きさを調節することで、特定の速度をもつ電子のみを取り出す装置を考えることができた。
- 速度v1[m/s]をもつ電子が半径r[m]の等速円運動を行うように、磁場の大きさを設定したとしよう。運動方程式、
より、[m/s]
これを上の「比電荷」の式に代入すると、 - 右辺にも「比電荷」が現れてしまったので、改めて整理して計算しなおすと、
[C/kg]
となった。右辺の諸量のうち、E,l,L,B,rは、すべて装置の設計上、操作可能な量であり、残るy1は実験結果として測定可能な量である。こうして、一様な磁場と一様な電場を持つ装置を接続することで、「比電荷」の測定が可能になった。 -
上の式の右辺の単位が、本当に[C/kg]となっていることを確認してみよう。
単位の変換 - 電場E ・・・ [N/C=V/m]
- 磁場H ・・・ [N/wb=A/m]
- 電流I ・・・ [A=C/s]
- 速度v1[m/s]をもつ電子が半径r[m]の等速円運動を行うように、磁場の大きさを設定したとしよう。運動方程式、
- 二枚の極板間に置かれた容器に霧吹きで油滴を吹き込む。はじめは電場をかけずに、油滴が自由落下するのを観測する。
どんなに上手に霧吹きを操作しても、個々の油滴の質量は異なるはずであるから、ここからの話は、たった一つの特定の油滴を追跡して観測する、というとても忍耐強い実験なのだということを理解する必要がある。
質量m[kg]のある特定の一個の油滴があったとする。はじめに作用する力は、下向きの重力mg[N]のみであるが、これが加速度を生じ、速度が増えるにしたがって、それに比例する空気抵抗の力が、運動と逆向きすなわち、上向きに作用し始める。これらは必ず、どこかで釣り合うようになるから、以降は、この油滴は等速直線運動によって落下し始める。この速度の大きさを、顕微鏡を使って、容器の壁面に刻まれた目盛を読み取ることで測定する。運動方程式は、下向きにy軸をとると、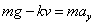
であるから、等速直線運動に移行したのちの速度(終端速度)を、v1とすれば、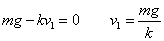 ・・・(1)
・・・(1)
となる。 - この容器内の霧にX線を照射すると、空気が電離され、正、または、負、のイオンが生じ、これらが油滴に付着して、それぞれの油滴を微小な荷電粒子に変えることができる。その上で、容器の上下方向に電場をかければ、個々の油滴粒子は、重力以外に、電場による力を受けることになるだろう。
今、仮に、電場は、上向き、y軸負方向、であったとしよう。油滴粒子には、正のイオン、または負のイオンのいずれが付着したかによって、電荷の符号もバラバラだから、上昇し始めるもの、加速して下降し始めるもの、様々であろうが、たまたま、注目していた油滴粒子は、上向きに運動し始めたとしよう。つまり、正に帯電していたから、電場と同じ向きに力を受けたのである。この粒子の持つ電荷をq[C]、加えた電場の大きさを、E[N/C=V/m]とすれば、新たな運動方程式は、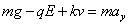
下向きにy軸をとっているから、電場の力は負、それによって上向きに速度をもったとすれば、空気抵抗は下向きだから正、右辺の加速度は、負の値となる。
ここでも、やがて「終端速度」に達するはずだから、それをv2とすれば、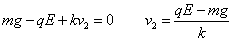 ・・・(2)
・・・(2)
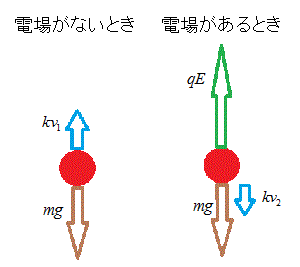
- ここで、もし、空気抵抗を表す比例定数kが、下降のときも上昇のときも一定だとすれば、(1)(2)式を用いて、ある特定の油滴粒子に着目している限りmは等しいのだから、その粒子の電荷qを算出することができる。すなわち、
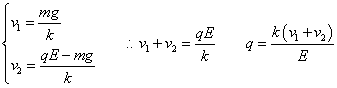
油滴の持つ電荷は、付着したイオンの「個数」によって、変動するだろう。しかし、そもそも空気の粒子が電離してイオン化したのだから、それは、- 「電子」をいくつか失って、陽イオンになったか、
- 「電子」をいくつか受け取って、陰イオンになったか、
でも、それを浮き彫りにするには、厖大な回数の観測が必要だったはずである。ミリカンは、おそらく次のようなデータを集めたのだろう。
これらのデータから得られたqの「最大公約数」が、「電気素量」と断定することになるのだが、上の例で、例えば、2番と6番のデータが欠落していたとしたら?、その「最大公約数」を3.2×10-19[C]と、過って断定してしまうことになるのである。だから、一つの油滴粒子を追跡するという、作業を、気の遠くなるほどの回数、繰り返す必要があったことが、わかるのである。番号 v1 v2 q 1 ・・・ ・・・ 6.4×10-19 2 ・・・ ・・・ 4.8×10-19 3 ・・・ ・・・ 9.6×10-19 4 ・・・ ・・・ 3.2×10-19 5 ・・・ ・・・ 12.8×10-19 6 ・・・ ・・・ 8.0×10-19 ・・・ ・・・ ・・・ ・・・
- 光を波動と考えては説明できない現象・・・「光電効果」→「光量子説」
- 光を粒子(量子)と考えるとうまく説明できる現象・・・「コンプトン散乱」
- では、逆に、粒子である筈の電子にも、波動性があるのではないか?・・・「ド・ブロイ波」
- 電子の波動性でうまく説明できる現象・・・「ボーアの電子モデル」
-
金属に光を当てると電子が飛び出す。
- しかし、その実験結果はいくつかの点で光を波動と解釈する限り説明不可能な点を含んでいた。
- ある一定の振動数以下の光を照射しても電子はひとつも飛び出さない。
電子が金属から飛び出してくるのは、その電子を金属に拘束している金属結合のエネルギーを超えるエネルギーが与えられ、その差が運動エネルギーとなると解釈される。
光が波動であるならば、波のエネルギーは振動数および振幅の関数だから、仮に振動数が小さくてもその強度(振幅)を高めることによって大きなエネルギーを電子に加えることができるはずだからこの事実は波動性では説明できない。 - ある一定の振動数を超える光を照射すると、電子は、その瞬間、直ちに飛び出してくる。
波は時間の関数であるから、それが伝えるエネルギーも時間的に増大し蓄積されるものと考えられる。
エネルギーの小さな波ならば電子が飛び出すのに必要なエネルギーが蓄積されるまでに時間がかかるはずだ。この結果も波動性では説明できない。 - ある一定の振動数を超える光であるならば、振動数を一定にすると、飛び出す電子の量(観測される電流の値)は光の強さに比例する。
この事実は、波動性からも説明が可能。
- ある一定の振動数以下の光を照射しても電子はひとつも飛び出さない。
- アインシュタインは「振動数νの光は、エネルギーhνを持つ『粒子』である」として、光電効果の実験結果を説明した。
光量子説 エネルギー 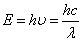
光は左に示されたエネルギー及び運動量をを持つ粒子である。
光量子は質量を持たず、したがって、
「運動エネルギー、位置エネルギー、などを観念することができない。運動量 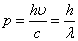
- 「光量子・光子」の持つエネルギーは振動数νのみによって決定される。光電効果で光電子が飛び出してくるのは、電子と光子の「衝突」として説明される。したがって、衝突する光子がある振動数(限界振動数)以下であれば、電子を金属の拘束から解き放って飛び出させることができない。
- 限界振動数を超える光ならば、たとえ弱い光でも、直ちに光電子が飛び出してくるのも、この「衝突」モデルで説明できる。光子は金属内の電子に衝突すると同時に、そのすべてのエネルギーを電子に与え、光子自らは消滅する、と考えられる。(完全弾性衝突では、力学的エネルギーが保存される。衝突した粒子が静止したとすれば、すべての運動エネルギー、すべての運動量が、衝突された粒子に「伝えられた」ことになる。光子では、質量が存在しないから、エネルギーと運動量をすべて失って、「消滅」する。)
- 光のエネルギーがhνの整数倍に「量子化」されているのは、光子という「粒子」が振動数のみによって決定される一定のエネルギーしかとり得ないからであり、光の「強さ」は光子の「個数」に対応する。光の強さを高めると光子の個数が増え、それと衝突して飛び出す光電子の数も増大する。
波はエネルギーを伝えることができるから、金属に拘束されている電子に大きなエネルギーを与えこれを金属外にはじき出すことは、波動性からも説明可能と思われた。
図で、Aは光電子を飛び出させる金属板、Bは飛び出した電子を受け止める「陽極」だが、AB間の電位差は可変抵抗PQによって相対的にどちらを高電位にすることもできる。Q側にスライドさせると、BはAより高電位になり、金属から飛び出した光電子は電場による力で加速されB極に容易に到達できる。P側にスライドさせると逆にAがBより高電位となるので、金属から飛び出した電子もよほど大きな運動エネルギーを持っていなければ、電場による力によって減速されてしまいB極に到達できなくなってしまう。
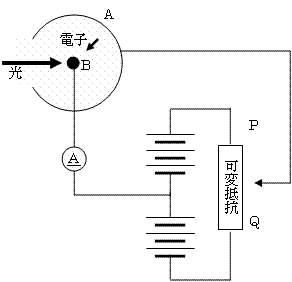
特定の振動数、特定の強さの光を照射させたまま、可変抵抗の端子をPからQにスライドさせていくと、初めて電流が流れ始めたときの電圧(阻止電圧)を記録することにより、光電子の持つ運動エネルギーの「最大値」を測定することができる。(自由電子は金属内部では、それぞれの瞬間にさまざまな大きさの運動エネルギーを持っており、これらが光子のエネルギーhνを受け取って、金属結合の拘束を解き放って金属外部に出る。その中でもっとも大きな運動エネルギーを持っていた電子のみがB極に到達できる。)
電子を金属に拘束しているエネルギー、すなわち、最大の運動エネルギーを持っていた電子を金属外部に引き出すのに必要なエネルギー、を「仕事関数」Wと呼ぶ。これは金属の種類によって固有の値をとる。
実験結果のグラフが、このように1次関数で表されることから、光量子説の正しさが裏付けられた。
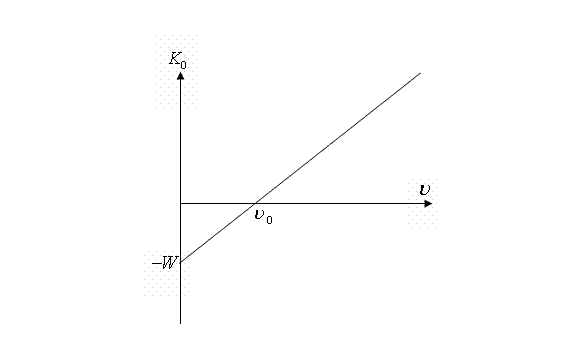
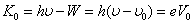
| 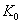 :光電子の運動エネルギーの最大値 :光電子の運動エネルギーの最大値
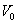 :初めて光電流が流れたときのAB間の電位差(阻止電圧) :初めて光電流が流れたときのAB間の電位差(阻止電圧)
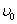 :限界振動数 :限界振動数
e:電気素量、電子1個の持つ電荷 |
-
可視光線よりもはるかにエネルギーの大きい電磁波であるX線を物体に照射する。物体を構成する原子の軌道電子はクーロン力で原子核と引き合っているだけだから、金属に拘束されている自由電子よりも容易に原子の外に飛び出さされる。
- エネルギー保存則(スカラー量)
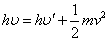 ・・・(1)
・・・(1)
- 運動量保存則(ベクトル量)
- x方向
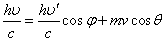 ・・・(2)
・・・(2)
- y方向
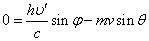 ・・・(3)
・・・(3)
- x方向
- 実験結果から得られた結論は、散乱X線の波長と入射X線の波長の差が、入射X線の波長に無関係で、散乱角ψのみの関数で表されたことである。すなわち、
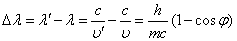 ・・・(4)
・・・(4)
- [計算]
- (2)(3)からθを消去する
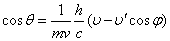
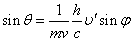
両辺を2乗して加えると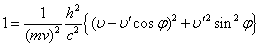
sinとcosの関係から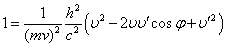
- 一方、(1)より
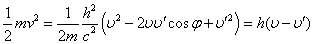
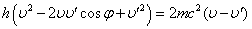
平方完成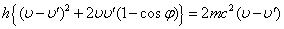
ここでΔλを導入する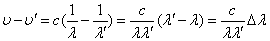
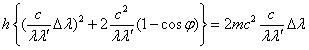
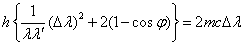
左辺第1項は充分に小さいと考えられるから、これを0とみなすと、(4)式が得られる。
- (2)(3)からθを消去する
光電効果では、電子を金属外に運び出すのにエネルギーが費やされ、光子自体はエネルギー、運動量ともに失って消滅したが、ここでは、光子と電子は、あたかも二つの粒子が弾性衝突を行うかのように、電子は弾き飛ばされ(反跳電子)、エネルギーと運動量が減少した光子もまた方向を変えて進行する(散乱X線)様が観察された。
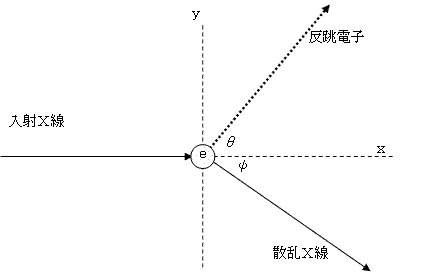
光量子説から導かれる「エネルギー」、「運動量」の定義を、ニュートン力学の「力学的エネルギー保存則」、「運動量保存則」に適用するだけで、この実験結果を完全に説明できたことが、光量子説の更なる裏づけとなった。
「波動」であると考えられていた光、X線などの電磁波に「粒子」としての性質がある、波動・粒子の「二重性」があると考えないと現象の説明がうまくできないことが明らかになってくると、今度は逆に、明らかに質量を持つ電子のような物質にも「波動」性があるのではないかと考えられ始めた。これをはじめに提起したのがド・ブロイである。
| 光量子説 | エネルギー | 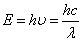 | 光は左に示されたエネルギー及び運動量をを持つ粒子である。 光量子は質量を持たず、したがって、 「運動エネルギー、位置エネルギー、などを観念することができない。 |
| 運動量 | 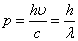 | ||
| 物質波 (ド・ブロイ波) | 運動量 | 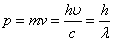 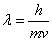 | 質量mをもち、速度vで運動する粒子には、 左に示された関係を満たす波長の波動が伴う。 (波長λは質量mに反比例するので、大きな質量を持った物質では 通常この波動が観測されることはない。) |
- 原子の内部構造について研究が重ねられ、中心に正に帯電した原子核と、その回りに負に帯電した電子が存在することが明らかになってきた。
しかし、これをクーロン力を向心力とする等速円運動と考えると、矛盾が生じる。すなわち、- 等速円運動では速度の大きさは変化しないが、ベクトル的には時間にともなって速度が変化する。荷電粒子の速度が時間的に変化すれば、周りに空間に変動する電場が生じ、これが変動する磁場を生じ、電場と磁場の相互作用によって、「電磁波」が発生するはずだ。
等速円運動する電子が、電磁波を放出すれば、それは次第にエネルギーを失い、回転半径が小さくなり、たちまち原子核に衝突してしまうだろう。しかしこのようなことは現実には起こっていない。
- 放電管の中の水素原子が発光するのは、外部からエネルギーを受け取って「励起」された電子がもとの軌道に戻るときに電磁波を放出してエネルギーを失うからだと考えられる。
しかし、クーロン力の位置エネルギーは半径に反比例する連続的な値をとりうるから、その電磁波はさまざまな波長を含む「連続スペクトル」を描くはずだ。しかし、実際に観測された波長は、整数nに関連付けられたとびとびの値しかとれない「線スペクトル」に、「量子化」されていた。
- 等速円運動では速度の大きさは変化しないが、ベクトル的には時間にともなって速度が変化する。荷電粒子の速度が時間的に変化すれば、周りに空間に変動する電場が生じ、これが変動する磁場を生じ、電場と磁場の相互作用によって、「電磁波」が発生するはずだ。
- ボーアは、ド・ブロイの「物質波」のアイディアから、軌道を回転する電子が「波動性」を有し、その回転軌道の長さ(2πr)が波長の整数倍であるという「定常波」の条件を満たす軌道にしか電子は存在し得ない、というきわめて簡単な仮定から出発して、現実に観測された水素原子のスペクトルをかなり高い精度で説明することに成功した。
- 量子条件:電子は不連続な値を持った(量子化された)いくつかのエネルギー状態しかとることができない。これを「定常状態」と呼ぶ。
- 振動数条件:電子がひとつの定常状態から別の定常状態に移るとき、光を放出する。その光(光子)のエネルギーは、二つの定常状態の持つエネルギーの差に等しい。
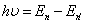
- [計算]
- 電子が半径rの円軌道を運行するとし、その軌道の長さが「電子波」が定常波を作る条件を満たしている、すなわち、波長の整数倍であるとすると、
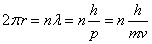 ・・・(1)
・・・(1)
- 運動方程式:クーロン力を向心力とする等速円運動
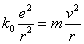 ・・・(2)
・・・(2)
- 電子の持つ運動エネルギー
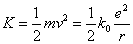
- 電子の持つクーロン力による位置エネルギー
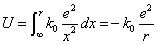
- 電子の持つ全力学的エネルギー
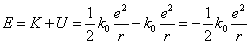 ・・・(3)
・・・(3)
- (1)(2)からvを消去
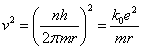
- rについて解くと
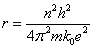
- これを(3)に代入、整数nに対応する定常状態のエネルギーとすると
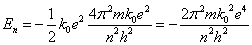
- 振動数条件より
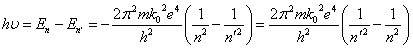
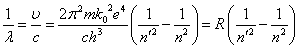
ここにRは「リュードベリ」定数と呼ばれる。 n'は励起された電子が、エネルギーを失って「落ち着く」先の軌道を表しており、1のとき「ライマン系列」、2のとき「バルマー系列」、3のとき「パッシェン系列」と呼ばれるスペクトル系列であるが、ボーアの計算式によりこれらの振動数分布をかなり高い精度で算出することができた。
- 電子が半径rの円軌道を運行するとし、その軌道の長さが「電子波」が定常波を作る条件を満たしている、すなわち、波長の整数倍であるとすると、
- ラザフォードは銀の薄膜にα粒子を衝突させ、その散乱を調べる実験をしていたが、その際、ほとんどのα粒子は散乱されずに通り抜けてしまうことを発見した。このことから原子の内部は、非常に隙間の多い構造を取っていることが明らかになった。核外電子を含めた原子全体の大きさと、その中心にある原子核の大きさとの比は、「校庭の真ん中に置かれたピンポン玉」にたとえられるという。
このように原子核が小さく密集した塊だとしたら、それを構成する粒子間にはどのような力が作用しているのだろうか?
中性子は電荷を持たないが、陽子は正電荷を持つから、複数の陽子を固めておくにはクーロンの斥力上回る大きな力が必要なはずである。 - 一方で、原子核の質量は、それを構成する陽子及び中性子の質量の和に比べて、わずかだか小さい値をとっていることがわかった(質量欠損)。
- アインシュタインは、質量とエネルギーとは同質であり、以下の式で示される関係で結ばれており、質量欠損に相当するエネルギーが核子(陽子及び中性子)間の結合に用いられている、とした。
質量とエネルギーの同質性 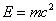
- 原子番号が同じ、すなわち陽子数が等しく、質量数が異なる、すなわち中性子数が異なる元素を「同位体」という。
このうち、安定に存在できず、放射性崩壊を起こして他の安定な元素に変わるものを「放射性同位元素」と呼ぶ。 - 放射性崩壊には、以下の3種類の形態がある。
崩壊の形態 放射能の実体 質量 電荷 エネルギー 透過力 α崩壊 ヘリウム原子核 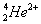
大 +2 大 小 β崩壊 電子 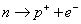
小
電子の質量は
陽子・中性子の1/1850-1 中 中 γ崩壊 電磁波
波長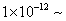 (m)
(m)0 0 小 大
- 放射性同位元素が崩壊する過程は「確率論的過程」であり、ある特定の原子が「いつ」崩壊を起こすかは決定することができない。
しかし、一定量の放射性同位元素についてみると、一定の時間内にどのくらいの割合(確率)で崩壊を起こすかは、その同位元素の不安定性によって決定されている。
放射性崩壊を起こして他の元素に変わるのだから、これは放射性同位元素が「減少」する過程であって、したがって、単位時間に減少する放射性同位元素の数、すなわち「減少速度[(個数)/s]」は、現在残っている放射性同位元素の数に比例する。すなわち、
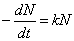
一階微分がもとの関数に比例する関数は、指数関数である。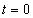 のとき、
のとき、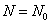 とすると、
とすると、
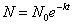
となる。
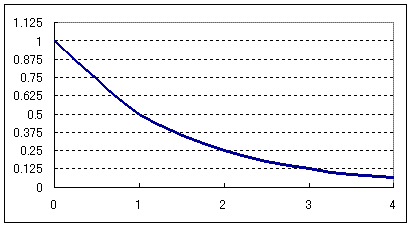
指数関数のグラフは、どの一部分をとっても、全体と相似であるという特質を持っている。はじめに立てた微分方程式が示しているように、現在量がある一定の割合まで減少する時間は常に等しい。そこで、「半減期」という概念が用いられるようになった。現在量が1/2になる時間をTとすれば、
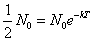 すなわち、
すなわち、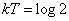 、これを用いてkを消去すれば、
、これを用いてkを消去すれば、
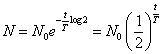
- 環境に存在する放射性炭素
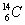 と、非放射性の通常の炭素
と、非放射性の通常の炭素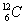 との存在比率は、放射性炭素の崩壊と生成の速度が平衡に達していて一定の値を示している。
との存在比率は、放射性炭素の崩壊と生成の速度が平衡に達していて一定の値を示している。
生きている植物は光合成と呼吸を通じての二酸化炭素のやりとりを行っているから、体内に外界の炭素 と同じ組成を維持している。しかし、植物が死ぬと、外界との炭素のやりとりがなくなるため、放射性炭素の濃度は、崩壊によって減少する一方である。
古代の地層から発掘された植物の化石、遺跡から発掘された木片など、植物の死骸に残留している放射性炭素の存在比率を調べれば、放射性炭素の半減期から、その植物が死んでからどれだけの時間が経過しているかを知ることができる。