- ビオ・サバールの法則、「右ねじの法則」とベクトルの外積
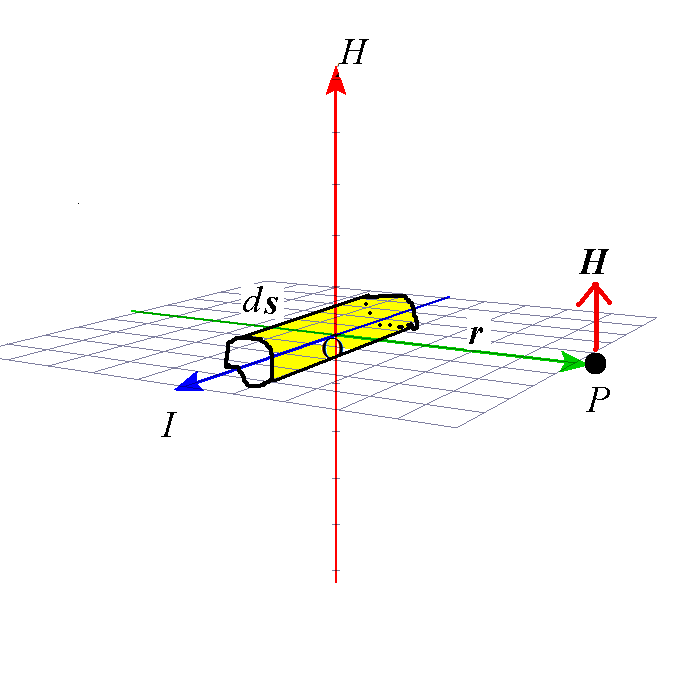
定常的に流れる電流の周りには「磁場」が発生する。その方向と大きさを示すのが、以下の式で示される「ビオ・サバールの法則」。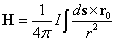 [N/wb=A/m]
[N/wb=A/m]
- ds : 電流の接線方向の「微小長さ」をあらわすベクトル。
- r0 : 電流「微小部分」から観測点Pに向かう単位ベクトル。
- r : 電流「微小部分」から観測点Pまでの距離(スカラー量)。
- I : 電流の大きさ(スカラー量)。
- H : P点に生じる「磁場」(ベクトル量)。
ベクトルの「外積」 a×b=|a||b|sinθ・n - θ : ベクトルaとベクトルbのなす角
- n : ベクトルaをベクトルbに重なるように回転させるのを「右ねじ」の回転に見立てたとき、「右ねじ」の進む方向の、単位ベクトル
- 直線電流、円形電流、コイルの作る「磁場」
上式を用いて計算すると、代表的な3種類の「磁場」の公式が得られる。
コイルは、円形電流を多数回繰り返したものと考えられるが、これを「無限化」すると、式から円の半径が「消えて」。つまり、充分に長いコイルであるならば、その「半径」は「磁場」に影響しない。無限に長く伸びた直線電流が、そこからr[m]離れた場所に作る磁場[N/wb=A/m] 半径r[m]の円形電流が、円の中心に作る磁場[N/wb=A/m] 単位長さ(1[m])あたりの巻き数がn0[1/m]であるコイルが、その内部の中心付近につくる磁場[N/wb=A/m] H=n0I
【参考:「磁場」の計算経過】- 「ビオ・サバールの法則」で「磁場」ベクトルの大きさを求めるには、スカラー形式の式、
[N/wb=A/m]
を用いる。 - 無限に長く伸びた直線電流が、そこからr[m]離れた場所に作る磁場
ここで、x=rtanθという置換積分を行うと、
x0=rtanθ0とすると、
x0→∞のとき、θ0→π/2であるから、 - 半径r1[m]の円形電流が、円の中心から円を含む平面に垂直な方向にr[m]離れた場所に作る磁場
まず、円を含む平面に平行な磁場の成分は、円の中心に関して対称な電流の微小区間が作る磁場とすべて打ち消しあうから、円を含む平面に垂直な成分のみについて考えればよい。
dsとr0は直交しているから、sinθ=1、
ここでは、半径r1の円弧の微小区間ds=r1dθという関係を用いている。
円の中心すなわち、r=0では、
となる。 - 半径a[m]、単位長さ(1[m])あたりの巻き数n0[1/m]の無限に伸びたコイルが、コイルの軸の中心上の観測点に作る磁場
円形電流の場合の結果から、半径a[m]の一巻きのコイルが、コイルの中心軸をx軸としたとき、場所xに作る磁場は、
であり、x軸上に取った微小長さdx[m]には、n0dx巻きのコイルがあるから、これについて積分すると
ここで、x=atanθという置換積分を行い、
x0=atanθ0とすると、
x0→∞のとき、θ0→π/2であるから、
この計算結果が示すように、無限の長さを持ったコイルを仮定すると、それが作る磁場の大きさは、コイルの半径に無関係であることがわかる。
【参考:「磁場」の公式の、おおざっぱな(!)理解】-
ビオ・サバールの法則
- 原点にある「大きさのない点」を「源」として、ある量Xが放出される。
- 半径rの球面上では、それは4πr2分の1に、薄まっている。
- だから、
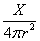
-
直線電流
- y軸上にある「幅のない線」を「源」として、ある量Xが放出される。
- 半径rの円柱面上では、それは2πr分の1に、薄まっている。
- だから、
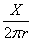
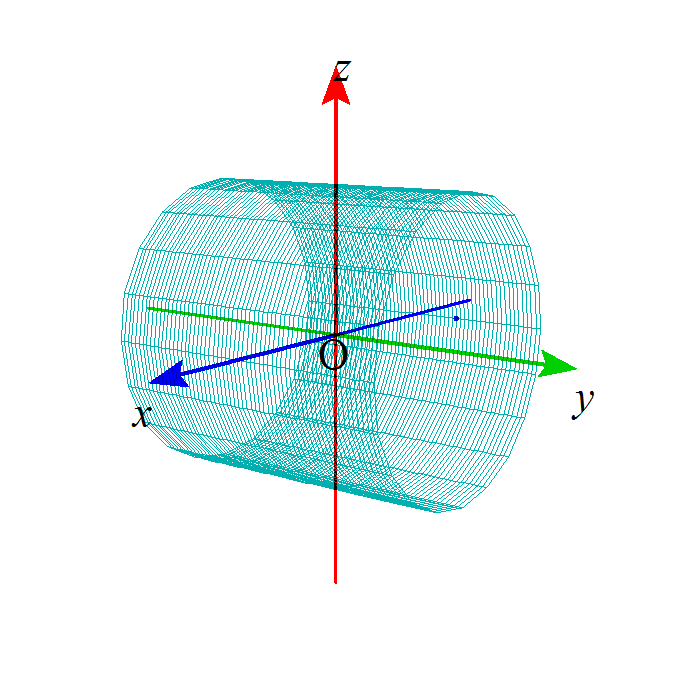
-
円形電流
- x-z平面上の原点中心、半径rの円周上に並んだ「大きさのない点」を「源」として、ある量Xが放出される。
- 原点では、「4πr2分の1」に薄められたものが、2πr倍に濃縮される。
- だから、
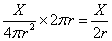
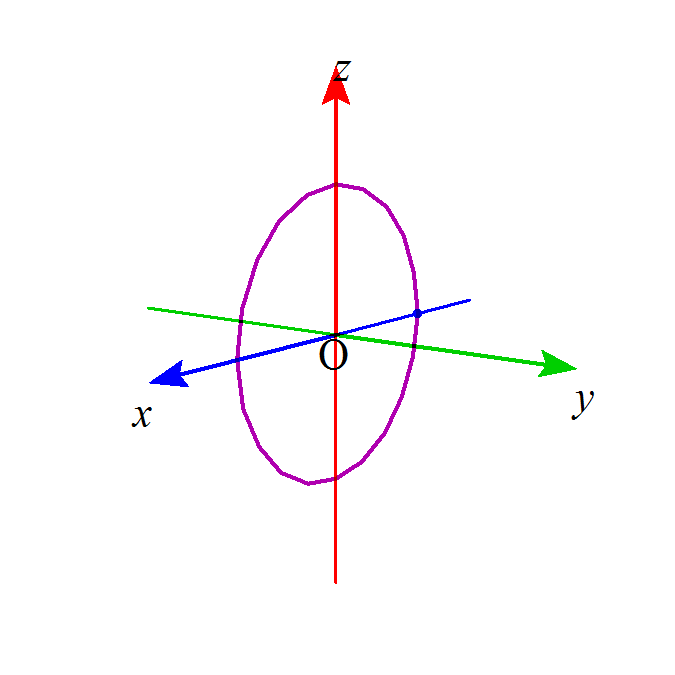
-
コイル
- 半径rの円柱面上に並んだ「幅のない線」を「源」として、ある量Xが放出される。
- 円柱の中心のy軸上では、「2πr分の1」に薄められたものが、2πr倍に濃縮される。
- だから、
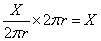
(少なくとも、半径rに無関係であることは、わかる。)
- 「ビオ・サバールの法則」で「磁場」ベクトルの大きさを求めるには、スカラー形式の式、
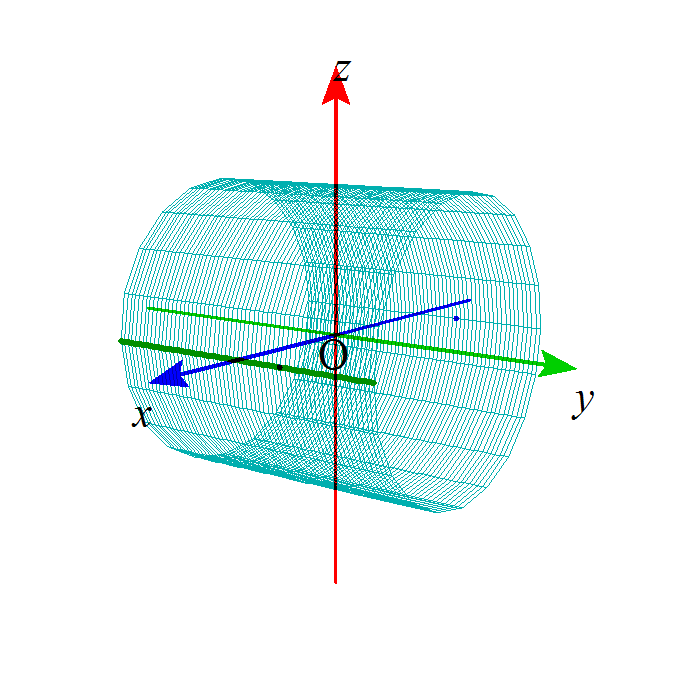
- 「磁場」の内部の運動する「荷電粒子」が受ける「力」:ローレンツ力
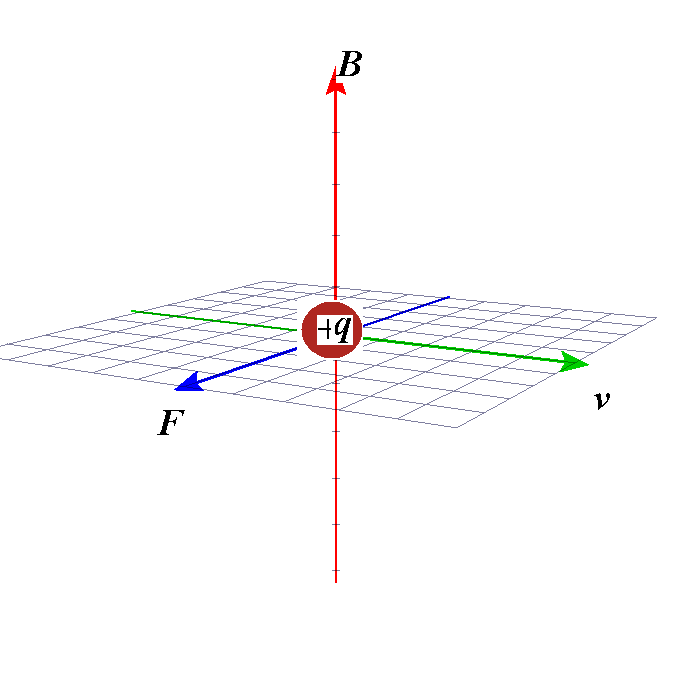
「ローレンツ力」を「外積」の式で書くとこうなる。
F=qv×B- F : 「荷電粒子」が受ける「力」(ベクトル量)[N]
- q : 「荷電粒子」のもつ「電荷」(スカラー量)[C]
- v : 「荷電粒子」の「速度」(ベクトル量)[C]
- B : 「磁束密度」(ベクトル量)[wb/m2]
「ローレンツ力」 F=Bqv - F ・・・左手「親指」
- B ・・・左手「人差し指」
- Iまたはv ・・・左手「中指」
- 「磁束密度」の定義
- 「磁場」のもう一つの定義
電場E 磁場H - +1[C]の点電荷に作用する「力」[N/C]
- 1[wb]のN極に作用する「力」[N/wb]
- 「電場」の定義に対応して、「磁場」を上のように定義することもできるた。
- ところが、どんなに小さく砕いても「N極」のみ、「S極」のみを取り出すことができない、つまり「単極の磁石を作ることができない」という特徴から、上の定義はあまり役に立たないことになる。
- そこで、「ローレンツ力」を用いて、次のように定義し直してはどうか?
- 「磁束密度」の定義
電場E 磁束密度B - +q[C]の点電荷が静止しているとき
- これに作用する「力」が、
F=qE
とかけるとき、E[N/C]を「電場」と呼ぶ。 - この式はベクトルの定数倍の式だから
EはFと同じ方向
- +q[C]の点電荷が速度vで運動しているとき
- これに作用する「力」が、
F=qv×B
とかけるとき、B[wb/m2]を「磁束密度」と呼ぶ。 - この式はベクトルの外積の式だから
F,B,vは「フレミング左手の法則」によって決まる
- こうすることによって、「電気力線」と「電場」、「磁束線」と「磁束密度」の関係もわかりやすくなる。
電場E 磁束密度B - 単位面積(1[m2])を垂直に横切る「電気力線」の本数が、その場所における「電場」Eをあらわすように決めればよい。
- すなわち、[1/m2]=[N/C]
- 単位面積(1[m2])を垂直に横切る「磁束線」の本数が、その場所における「磁束密度」Bをあらわす。
- だから、B[wb/m2]、
「磁束」Φ[wb]とは、「磁束線」の本数そのものだ!
- 「電場」と「磁場」の大きな違い
たとえば直線電流のまわりの磁力線・磁束線は、電流を中心にした「同心円」を描く。電場 磁場 - 「電気力線」は「正電荷」から出て「負電荷」に入る。
- 「湧き出し口」と「吸い込み口」のある「場」である。
- 「磁力線・磁束線」は「N極」から出て「S極」に入る。
- しかし、「N極」と「S極」は切り離すことができないから、「循環型」の「場」になる。
電場 磁場 - 「荷電粒子」が「電場」から「力」
F=qE
を受けると、力の方向に移動することになるから、この「力」は「仕事」をする。 - 「電位」とは「電場」による「力」に逆らって、「荷電粒子」を運ぶ「仕事」から定義された。
- 運動する「荷電粒子」が「磁場」から「力」
F=qv×B
を受けると、この力は運動方向と垂直だから、「仕事」をしない。 - したがって「磁場」では、「電位」に相当するような「位置エネルギー(ポテンシャル)」を考えることができない。
- 「磁場」H[N/wb]と「磁束密度」H[wb/m2]の関係
- B=μ0H ・・・ (μ0 : 真空の透磁率)
- ともにベクトル量であるから、
- 大きさは、μ0倍、
- 方向は同じ。
- 「磁場」のもう一つの定義
- 一様な磁場の内部で「ローレンツ力」を受ける「荷電粒子」の運動
- +q[C]の電荷を持った質量m[kg]の荷電粒子が、磁束密度B[T=wb/m2]の一様な磁場に、磁束の方向に垂直な方向に、速度v[m/s]で、進入したとする。
運動する荷電粒子は磁場からローレンツ力を受け、その速度に対してつねに直交する方向に一定の大きさの力を受けることになるので、等速円運動を行う。 - 運動方程式
- 半径:
[m]
- 角速度:
[(rad)/s]
- 周期:
[s]
- 半径:
- +q[C]の電荷を持った質量m[kg]の荷電粒子が、磁束密度B[T=wb/m2]の一様な磁場に、磁束の方向に垂直な方向に、速度v[m/s]で、進入したとする。
- 【例題】「トムソンの実験(比電荷の測定)」
- 速度v1[m/s]の電子を、長さl[m]の一様電場E[N/C=V/m]に、電場ベクトル(電気力線)に垂直な方向から進入させる。電子は電場からの一定の力により進路を曲げられ、放物運動を行うだろう。その進路のずれはわずかだが、これを電場のない空間を直進させることで拡大し、十分に離れたスクリーン上で検出することができる。
電子の進入速度v1[m/s]がわかっていれば、ここから、電子の比電荷(電子の持つ電荷[C]の、質量[m]に対する比)を算出することができる。
まず、ここまでを確認しよう。電子の質量をm[kg]、電荷を-e[C]とする。
- 電子の進行方向をx軸の正の向き、一様電場の向きをy軸の負の向きとする。
- 電場に進入した電子は、電場からy軸の正の向きにeE[N]の力を受ける。電子の質量は十分小さく、重力は、ここで問題にしている力に比べ無視できるとする。運動方程式
eE=ma
より、電子はy軸方向には、等加速直線運動を行う。
x軸方向には、なんらの力も作用していないから、初速度v1[m/s]で等速直線運動を行う。
vx=v1
x=v1t - 長さl[m]の一様電場を抜け出るまでに生じたy方向の進路のずれは、上の式でx=lのときのyを計算すればよい。これをy0[m]とすると、
一様電場の長さl[m]のちょうど中央から計って長さL[m]の場所にあるスクリーン上で検出される進路のずれy1[m]は、電子が一様電場を脱出するときの進行方向がx軸となす角をθとすれば、 - 一方、tanθは電子が一様電場を脱出するときのvyとvxの比であるから、
- 以上をまとめると、
- こうして、比電荷e/mは、
[(C/kg)={m・(m/s)2}/{(N/C)・m2}={m・(m/s)2}/{(kg・m/s2・C)・m2}]
となる。
右辺の各変数のうち、E,l,Lは実験装置の設計によって決定でき、y1は観測結果から得られる。したがって、電子が電場に進入する速度v1さえ明らかになったら、「比電荷」の算出が可能になることになる。19世紀末から20世紀初頭にかけて活躍したJ.J.トムソンが、どのようにして既知の速度の電子を発生させることができたのであろうか?
ここから先が、一様磁場における電子の等速円運動の問題である。
なお、「比電荷」とはわかりにくい概念だが、電子の実在については確証を得たものの、質量・電荷ともにあまりにも小さい粒子であるために、その測定は困難を極めた。歴史的には、まず、トムソンが「比電荷」を計算し、ついでミリカンが「油滴実験」によって電子の質量を統計的手法をもって確定し、ここから間接的に電子の電荷、すなわち「電気素量」が算定された。
-
紙面の裏から表へ向かう方向に一様な磁場B[T=wb/m2]がある「箱」を考えよう。この箱の側面には
2r[m]の距離を隔てて二つの「穴」があけられている。一方の穴、「入口」からは、さまざまな速度をもった電子が、箱の壁面に垂直に進入する。箱に進入した電子は、磁場から「ローレンツ力」を受け、その持っていた速度に応じたさまざまな半径の等速円運動を行うだろう。
これらの電子のうち、半径r[m]の等速円運動を行うような速度をもった電子のみが、「出口」の穴から箱の外に出ることができる。
こうして、一様な磁場Bの大きさを調節することで、特定の速度をもつ電子のみを取り出す装置を考えることができた。
- 速度v1[m/s]をもつ電子が半径r[m]の等速円運動を行うように、磁場の大きさを設定したとしよう。運動方程式、
より、[m/s]
これを上の「比電荷」の式に代入すると、 - 右辺にも「比電荷」が現れてしまったので、改めて整理して計算しなおすと、
[C/kg]
となった。右辺の諸量のうち、E,l,L,B,rは、すべて装置の設計上、操作可能な量であり、残るy1は実験結果として測定可能な量である。こうして、一様な磁場と一様な電場を持つ装置を接続することで、「比電荷」の測定が可能になった。 -
上の式の右辺の単位が、本当に[C/kg]となっていることを確認してみよう。
単位の変換 - 電場E ・・・ [N/C=V/m]
- 磁場H ・・・ [N/wb=A/m]
- 電流I ・・・ [A=C/s]
- 速度v1[m/s]をもつ電子が半径r[m]の等速円運動を行うように、磁場の大きさを設定したとしよう。運動方程式、
- 速度v1[m/s]の電子を、長さl[m]の一様電場E[N/C=V/m]に、電場ベクトル(電気力線)に垂直な方向から進入させる。電子は電場からの一定の力により進路を曲げられ、放物運動を行うだろう。その進路のずれはわずかだが、これを電場のない空間を直進させることで拡大し、十分に離れたスクリーン上で検出することができる。
- 運動する「荷電粒子」が「磁場」から「ローレンツ力」を受けるならば、導線の中を一定方向に運動している「荷電粒子」の集合である「電流」にも、「力」が作用するはずだ。
もちろん、「実際に」運動しているのは「負」の荷電粒子である「自由電子」であるが、これとは逆向きに「架空」の「正電荷」が運動していると思えばよい。
- では、「電流」I[A]が「磁場」と垂直に、定常的に流れる導線l[m]区間に作用する力を「ローレンツ力」の式から求めよう。
- 電流I[A=C/s]とは、導線のある断面を1秒間にI[C]の電荷が通過することを意味する。
- 電荷の平均的な速度をv[m/s]、導線の断面積をS[m2]とすれば、体積vS[m3]の円柱に電荷I[C]が存在している計算になる。
- 一方で、長さl[m]の導線区間に存在する電荷が、q[C]であるとすれば、両者の「電荷密度」を等式で結んで、
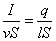
- こうして、「ローレンツ力」F=Bqvのqvの代わりに、Ilを代入すればよいことが分かった。
磁場に垂直に流れる電流に作用する力
(フレミング左手の法則) F=BIl- F ・・・左手「親指」
- B ・・・左手「人差し指」
- I ・・・左手「中指」
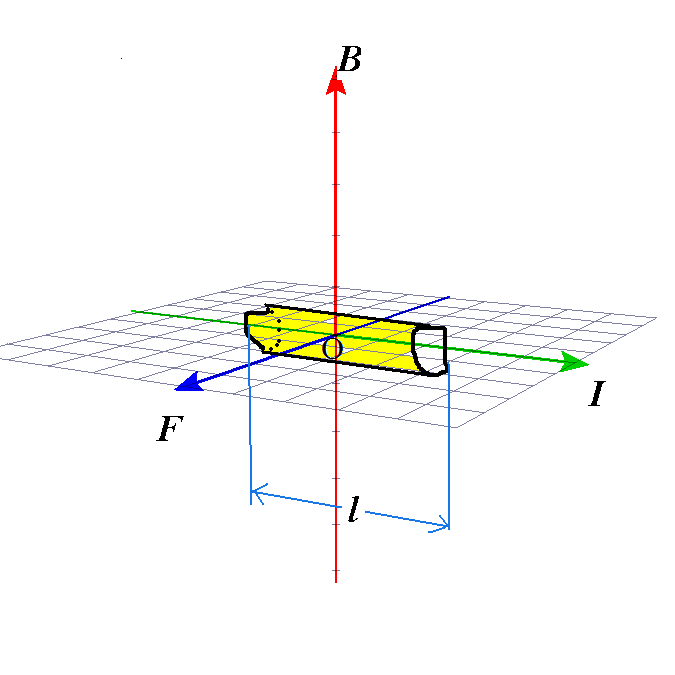
- 電流I1[A]と電流I2[A]が距離r[m]を隔てて、ともに紙面裏から表に向かう同じ向きに流れている。(左図)
- I1がI2の場所に作る「磁場」H1は上向き、したがって、I2のl[m]区間がこれから受ける力Fは左向き。
- I2がI1の場所に作る「磁場」H2は下向き、したがって、I1のl[m]区間がこれから受ける力Fは右向き。
- 二本の導線は、互いに引き合う。
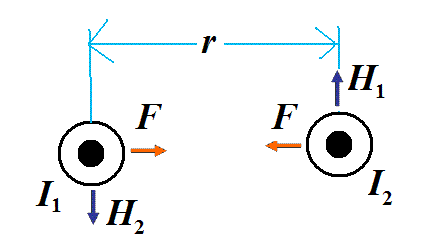
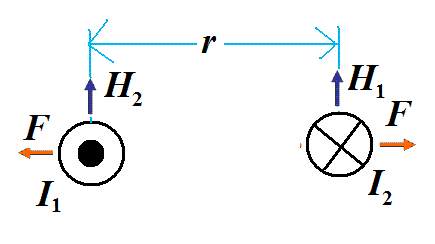
- 電流I1[A]と電流I2[A]が距離r[m]を隔てて、I1は紙面裏から表、I2は紙面表から裏に向かう逆向きに流れている。(右図)
- I1がI2の場所に作る「磁場」H1は上向き、したがって、I2のl[m]区間がこれから受ける力Fは右向き。
- I2がI1の場所に作る「磁場」H2は上向き、したがって、I1のl[m]区間がこれから受ける力Fは左向き。
- 二本の導線は、互いに斥け合う。
- その大きさを計算すると、
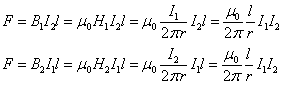
- 実はここから、電流の単位「アンペア」が定義されている。
「アンペア」の定義 - 互いに1[m]隔てて平行に置いた導線に、同じ大きさの電流を流す。
- 各導線1[m]区間に働く力が2×10-7[N]になる電流を1[A]とする。
- 計算してみると、
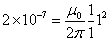
- すなわち、真空の透磁率μ0とは、4π×10-7
| 「電磁誘導」 |
|
- 誘導起電力の計算
次のような「閉回路」を考える。一様な磁場B[T=wb/m2]を横切る長方形の回路で、一辺が摩擦なく自由に動かせる導体棒でできている。導体棒を左右に動かすことで、この回路が横切る磁束の大きさを変化させることができる。
回路が横切る磁束をΦ[wb]、回路の面積をS[m2]とすると、これらはいずれも時間t[s]の関数であるが、B[T=wb/m2]は時間にかかわらない定数である。
Φ=BS
導体棒の移動速度をv[m/s]とし、右向きを正とすると、単位時間当たりの回路の面積の増加率、すなわちdS/dtは、dS/dt=lvであるから、
こうして、導体棒の両端には、大きさBlv[V]の誘導起電力が発生する。 - 誘導起電力の「マイナス」の意味を、具体的に考える
- vが正、すなわち、導体棒が右向きに運動するとき
- dS/dt>0であるから、上向きの磁束が増加する。
- この変化を「打ち消す」とは、下向きの磁束を増加することであるから、右ねじの法則(ビオ・サバールの法則)によれば、回路に時計回りの電流が発生すればよい(誘導電流)。
- このような誘導電流が発生するとすれば、導体棒が電池の役割を果たしたと考えられ、P点が+極、Q点が−極となるよう、導体棒に起電力が発生したといえる(誘導起電力)。Pに対するQの電位が「負」である、これがVの符号が「−」の意味である。
- ところで、このような誘導電流が発生すると、導体棒は、磁場から左向きの「力」を受ける(フレミングの左手の法則)。導体棒の右向きの動きは、これによって「減速」される。
- vが負、すなわち、導体棒が左向きに運動するとき
- dS/dt<0であるから、上向きの磁束が減少する。
- この変化を「打ち消す」とは、上向きの磁束を増加することであるから、右ねじの法則(ビオ・サバールの法則)によれば、回路に反時計回りの電流が発生すればよい(誘導電流)。
- このような誘導電流が発生するとすれば、導体棒が電池の役割を果たしたと考えられ、P点が−極、Q点が+極となるよう、導体棒に起電力が発生したといえる(誘導起電力)。Pに対するQの電位が「正」である、これがVの符号が「+」の意味である。
- ところで、このような誘導電流が発生すると、導体棒は、磁場から右向きの「力」を受ける(フレミングの左手の法則)。導体棒の左向きの動きは、これによって「減速」される。
- vが正、すなわち、導体棒が右向きに運動するとき
- 回路のエネルギーの収支について
- 誘導起電力の大きさ[V]
|V|=Blv
- 誘導電流[A]
- 誘導電流が磁場から受ける力[N]
- 誘導電流が磁場から受ける力に逆らって、導体棒を速度v[m/s]で
 t[s]間動かすのに必要な仕事[J]
t[s]間動かすのに必要な仕事[J]
- 誘導電流が
 t[s]間にする仕事(抵抗Rに発生するジュール熱)[J]
t[s]間にする仕事(抵抗Rに発生するジュール熱)[J]
- 誘導起電力の大きさ[V]
- 電磁誘導の、ローレンツ力による説明
- 電位[V=J/C]は、単位正電荷あたりのエネルギーを表す。起電力[V]は、「もしその両端に抵抗を接続すれば、電流が流れ、抵抗においてジュール熱の発生という仕事をなしうる、潜在的なエネルギー」といえる。
- 高い場所に存在している物体は、低い場所に存在している物体に比べて、より大きな「重力による位置エネルギー」を[J]持っており、これは実際に二つの物体を落下させてみて、その「破壊力」を比較してみるまでもなく、明らかにすることができる。
- 電気店の店頭に陳列してある「電池」は、メーカーが保証するとおり、しかるべき「起電力」を有しているはずだが、これを購入して持ち帰り、例えば懐中電灯に装着して確かに電球が灯る、すなわち「閉回路」に「電流」を流すことができることが確認できない限り、確かに「起電力」を有しているということが立証できない。
- 上の例で、
- 誘導電流が生じたのは、もちろん、閉回路があったからである。
- しかし、仮に、導体棒PQを閉回路に接続しないまま磁場の内部を同じように移動させておき、
ある瞬間、突然に、閉回路に接続したとしたら、接続するや否や、その瞬間に誘導電流が流れだすはずではないか? - ということは、閉回路がなくとも、磁場の内部を導体棒が移動するだけで、すでにPQ間に誘導起電力が発生していた(!)と言えなければ、おかしいではないか?
- 導体棒に誘導起電力が発生していることを、閉回路の助けを借りずに、誘導電流の助けを借りずに、説明することはできないであろうか?
- 導体棒が右向きに速度v[m/s]で移動
- 導体棒の内部には無数の自由電子が存在するが、それらすべてはP→Q方向のローレンツ力を受ける
- 自由電子はQ側に移動し始め、Q側は電子が過剰な状態、P側は電子が不足する状態、が発生する。すなわち、Qは負に帯電、Pは正に帯電する。こうしてPからQに向かう方向に電場が発生した。
- まだ、Qに到達していなかった電子には、電場からの力がQ→P方向に作用する。
- これら二つの力、ローレンツ力と電場からの力がつりあい、これ以上の電荷の移動は妨げられる。
- ローレンツ力[N]:F=Bev
- 電場からの力[N]:F=eE
Bev=eE
Bv=E
Eは一様電場[N/C=V/m]であるから、PQ間の電位差[V]は、
V=El=Blv
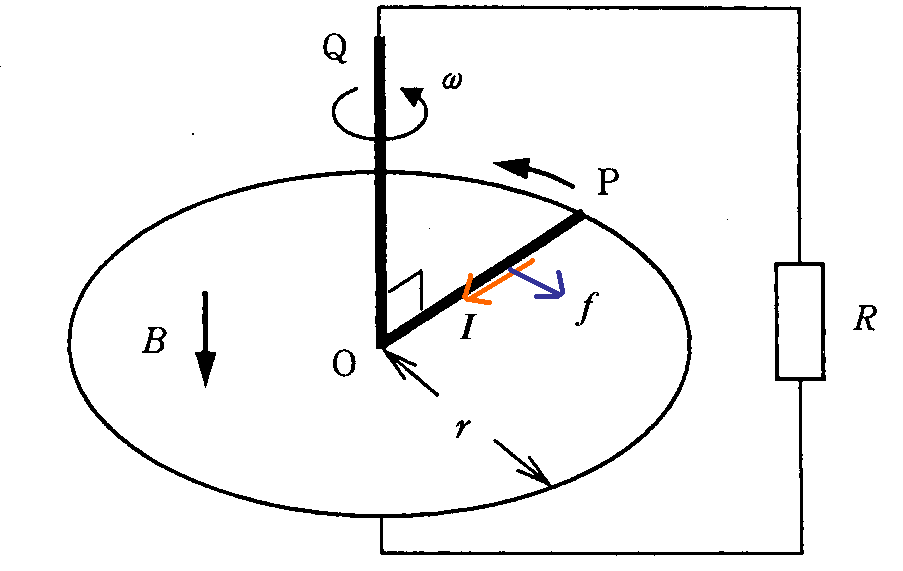
- 【例題】一巻きの円形コイルに沿って移動する導体棒
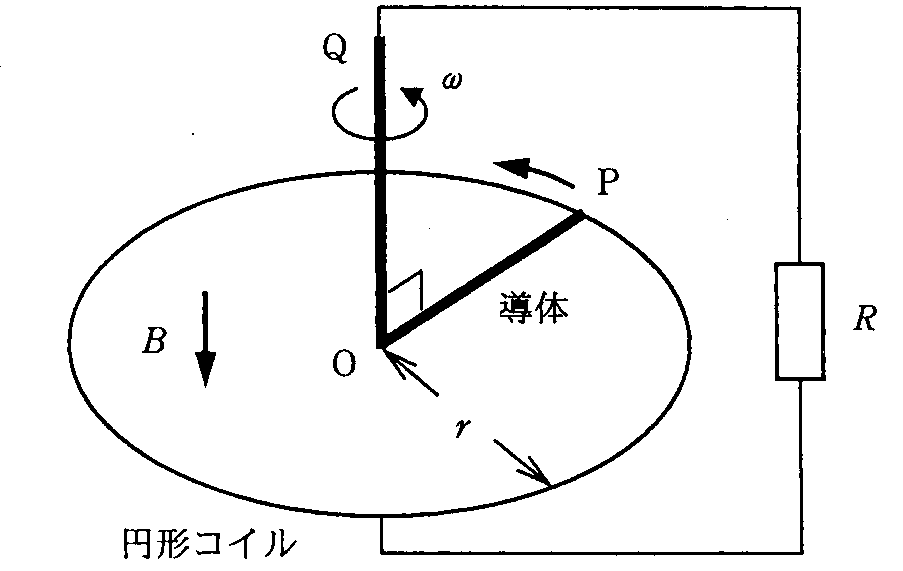
- 一巻きの円形コイルを、上から下に垂直に貫く磁束密度B[T=wb/m2]の磁場がかけられている。
- QOPのL字型をした導体QOPを、Pを円形コイルに滑らかに接触させたまま、円形コイルに垂直な軸OQを中心にして、上から見て反時計回りに、一定の角速度ω[1/s]で回転させる。
- 円形コイルが一回転する間に抵抗Rでの消費されたジュール熱を求めよ。
- 円形コイルを一回転させるために必要な外力の仕事を求めよ。
- (円形コイルに沿って電流が流れるわけではないから、これは「閉回路」ではない?導体棒OPが回転しても、その「面積」は減りも増えもしない?・・・だから、OP間に「誘導起電力」が発生する理由は、「ローレンツ力」によって説明するしかない!)
- 導体棒OPが上から見て反時計回りに回転すると、その内部に無数に存在する「自由電子」には、
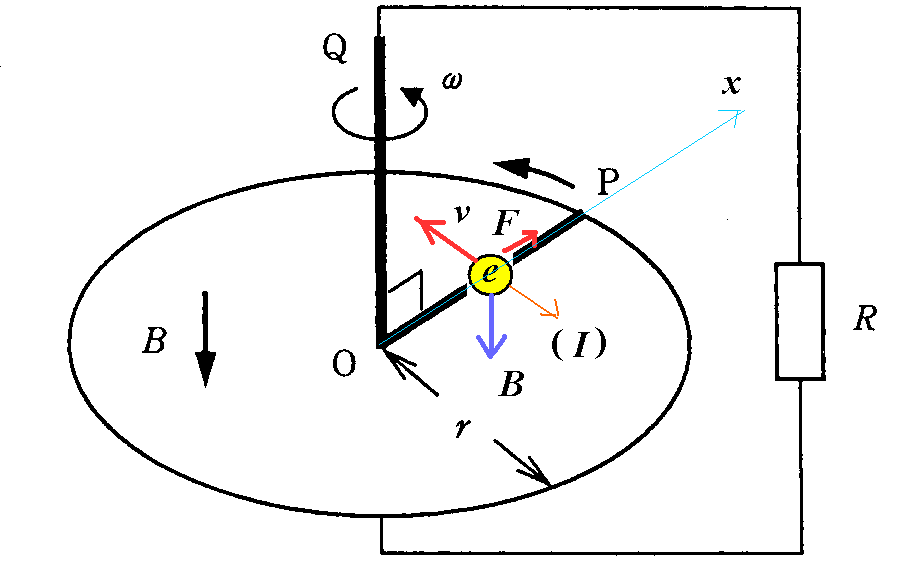
O→P方向に「ローレンツ力」が作用する。- 「自由電子」のもつ速度ベクトルは、OPに垂直で、図の左上向き。
- 「自由電子」は負の荷電粒子だから、「フレミング左手の法則」適用に当たっては、「電流」Iはその反対、図の右下向き、にしなければならない。
- こうして、「自由電子」の流れ、
O→P→(円形コイル)→R→Q→O
が生じる。
「電流」は正の電荷の流れであるから、その反対で、
O→Q→R→(円形コイル)→P→O
この「回路」で、電源として起電力を供給しているのは、導体棒のOP部分であるから、これを「電池」に見立てると、- 「外部抵抗」Rに向かって「電流」が流れ出しているOが「正極」、
- 「外部抵抗」Rから「電流」が流れ込んでいるPが「負極」、
- OがPより、高電位である、
- ところで、今、現にPからOに向かって電流が定常的に流れているのならば、OP間には逆に、
- PがOより、高電位である、
(「内」と「外」とでは、話が「あべこべ」になる!、電池の中では、電流は、マイナスからプラスに流れる!)
この電場をE[N/C=V/m]とすると、この「電場」が「自由電子」に及ぼす力が「ローレンツ力」そのものだ!、と考えて、
eE=Bev - 問題なのは、導体棒を平行に動かすのとちがって、Oを中心に回転させているから、場所によって「速度」vが異なることだ!
だから、
E=Bv
は場所によって異なり、「一様電場」ではない。 - OからPに向かう方向にx軸をとる。
「場所」x[m]地点では、v=xωであるから、
E=Bxω
したがって、OP間に生ずる「誘導起電力」の大きさV[V]は、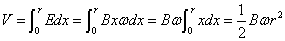
- 抵抗Rを流れる「誘導電流」I[A]は、
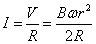
抵抗Rの消費電力P[W=V・A=(J/C)・(C/s)=J/s]は、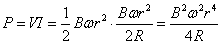
導体棒が一回転するのに要する時間は、2π/ω[s]だから、抵抗Rで消費されるジュール熱Q[J]は、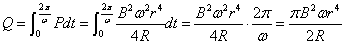
- 一方、導体棒OPのx[m]地点付近の微小長さ
 x[m]が磁場から受ける「力」[N](フレミング左手の法則)は、
x[m]が磁場から受ける「力」[N](フレミング左手の法則)は、
f=BI x・・・図の右下向き
x・・・図の右下向き
したがって、これとつりあうようにくわえなければならない「外力」は、同じ大きさで、方向は、図の左上向き。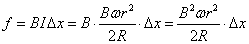
この力が、円形コイルが一周回転する間にする仕事w[J]は、半径x[m]の円周の長さ2πx[m]をかければよいから、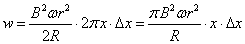
導体棒OP全体については、これを0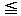 x
x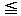 rで積分して、
rで積分して、
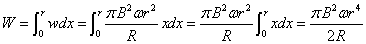
- こうして、Q=Wが導かれた。
- 自己誘導
- 閉回路に電流が流れると、まわりの空間に磁場が発生する(ビオ・サバールの法則)。
- 一方、磁場が変動すると、誘導起電力が生じ、閉回路には誘導電流が流れる(電磁誘導)。
- したがって、閉回路を流れる電流が変動するとき(例えばスイッチを閉じたとき、開いたとき、など)、電流の変化が磁場の変化をもたらし、磁場の変化が誘導起電力を生じ誘導電流が流れる。ひとつの回路の中で、電流の変化がまた電流の変化を導く、という複雑な過程が発生する。これを自己誘導という。
導線同士が十分に離れた普通の閉回路では、磁場の変化も誘導起電力も微弱であろうから、通常は問題にならないが、コイルのように、導線を繰り返し巻きつけることで、一本の磁束が多数回、閉回路を横切るような構造の場合、これによって生じる自己誘導はかなり大きなものになるだろう。 - レンツの法則
ここで、磁束Φ[wb]は、磁束密度B[T=wb/m2]、閉回路の面積S[m2]、さらに、磁場H[N/wb=A/m]、透磁率μを用いて、
Φ=BS=μHS
とかけるが、 - ビオ・サバールの法則
より、磁場は電流に比例し、したがって磁束も電流に比例するから、
Φ=LI
と書けることになる。この比例係数Lを回路の「自己インダクタンス」[H=wb/A]と呼ぶ。
- コイルの場合について考える。
断面積S[m2]、長さl[m]、巻き数n、単位長さあたりの巻き数n0=n/l[1/m]、とすると、- 1巻き分の回路が横切る磁束
Φ0=BS=μHS=μn0IS - コイル全体で考えると、
Φ=nΦ0=nμn0IS=n0l・μn0IS=μn02lS・I
となり、
L=μn02lS - 1巻き分の回路が横切る磁束
- 自己誘導の例
- コイル、抵抗、直流電源、を直列接続した回路に、スイッチを入れた直後、どのような電流が流れるか?
- キルヒホッフ第2法則より、
- コイルの自己インダクタンスをL[H]とすると、
両辺をRで割ると、
- ここで次のような変数変換を行う。
この式は、tの関数Iとその1階微分dI/dt、および定数項からできている。定数項を除去するために次のような変数変換を行う。
両辺をtで微分すると、定数項は消えるから、
であるから、上の式は次のように書きかえられる。
- すなわち
「もとの関数が、その時間による1階微分に比例し、符号は逆」であるから、 これをみたすtの関数iは、
cは積分定数。 - スイッチを入れた瞬間t=0においてI=0、すなわち、i=V/Rであるから、積分定数cは次のように定まる。
(あるいは、十分時間経過後、すなわち、t→∞において、コイルには抵抗はないのだから、I=V/R、すなわち、i=0と考えるべきか?)
よって、
Iに戻すと、
- こうして、この回路にスイッチを入れてから時間の経過とともに、電流がどのように変化するのかを表す関数が得られた。
直流電源と抵抗のみの回路ならば、スイッチを入れた瞬間に電流はV/Rまで跳ね上がるだろう。コイルがつながれることで、その反応に「遅れ」が生じ、充分に時間が経過した後、V/R[A]の定常電流に達する。これが、「自己誘導」の効果の一つの現れである。
- キルヒホッフ第2法則より、
- コイル、抵抗、直流電源、を直列接続した回路に、スイッチを入れた直後、どのような電流が流れるか?
- コイルが自己誘導によって蓄えるエネルギー
上のグラフからわかるように、スイッチを入れた後しばらくの間、電源はエネルギーを供給しているにもかかわらず、電流が小さく抑えられているため、抵抗で発生するジュール熱は小さいままである。これは、コイルが、エネルギーを蓄える機能を持っていると、考えざるを得ない。
[J]
- 相互誘導
- 二つの閉回路が、それらをつらぬく磁束を共有していたとしよう。一方の回路の電流が変動し、それが作る磁場が変動すれば、他方の回路にとっても磁場が変動したことになるから、誘導起電力、したがって誘導電流が生じる。この現象を「相互誘導」と呼ぶ。
- 二つのコイル、コイル1、コイル2について考える。
コイル1 コイル2 単位長さあたりの巻き数[1/m] n1 n2 長さ[m] l1 l2 断面積[m2] S1 S2 - コイル1に電流I1を流したとき、この電流がコイル1、コイル2に作る磁場H1は、
H1=n1I1 - 透磁率をμとすれば、磁束密度は、B1は、
B1=μn1I1 - コイル2の1巻きあたりの磁束は、
Φ0=B1S2=μn1I1S2
コイル2全体の磁束は、
Φ=n2l2Φ0=n2l2μn1I1S2 =μn1n2l2S2・I1 - ここで、
M=μn1n2l2S2
とすると、
Φ=MI1
となり、 - I1が変動するとき、コイル2に生じる誘導起電力V2は、
と表すことができる。このMを「相互インダクタンス」と呼ぶ。
- コイル1に電流I1を流したとき、この電流がコイル1、コイル2に作る磁場H1は、
- ここでも、相互誘導の様子を次のような回路で見てみよう。コイルL1,L2が、磁束を共有するように重ねられているとする。
- 下の回路に流れる電流は、「自己誘導」のところで見たように、
- これによって、上の回路のコイル2の両端に生じる誘導起電力は、
上の式の最後の変形は、以下の関係を用いた。
M=μn1n2l2S2
L1=μn12l1S1 - したがって、上の回路に流れる、相互誘導による誘導電流は、
- 下の回路のスイッチを入れた瞬間に、上の回路には、下の回路とは逆向きの最も大きい電流が流れ、時間の経過とともに、減衰し、やがて、定常状態では電流が流れなくなることがわかる。
- 下の回路に流れる電流は、「自己誘導」のところで見たように、
- LC振動回路
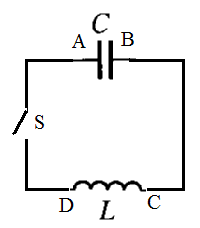
- 時刻t=0に、コンデンサのA極板に+Q0[c]、B極板に-Q0[c]、を蓄えてスイッチを入れる。
- 時刻tにおけるコンデンサのA極板の電荷をQ[c]、コイルをDからCに向かって流れる電流をI[A=c/s]とすると、
(電流は、正電荷が極板から「流出」する方向だから)
 ・・・(1)
・・・(1)
- コイルの長さl[m]、断面積S[m2]、単位長さ(1[m])当たり巻き数n0とすると、
- コイルが作る磁場H[N/wb]は、H=n0I
- コイルが作る磁束密度B[wb/m2]は、B=μ0n0I
- コイル全体では、1本の磁束線がそれぞれn0l回この磁場を横切ることになるから、コイルの全磁束Φ[wb]は、Φ=n0lSB=μ0n02lSI
- こうしてコイルの作りだす磁束が電流に比例することから、その比例係数μ0n02lSを「自己インダクタンス」Lと呼ぶことにした。
- したがって、Φ=LI
- コイルの両端に生じる誘導起電力VL[V](Dを基準にしたCの電位)は、
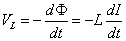 ・・・(2)
・・・(2)
(1)(2)より、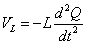
- キルヒホッフ第2法則より、VC-VL=0、すなわち、
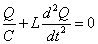
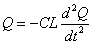 ・・・(3)
・・・(3)
こうして、時間の関数Qは、その2階微分が関数自身に比例し、符号が逆であるから、「単振動」を行うことがわかった。 - 時刻t=0で、Q=+Q0であること(初期条件)から、
Q=Q0cosωt
とおくことができる。これを2階微分すると、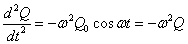
であるから、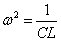 すなわち
すなわち 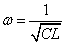 [(rad)/s]
[(rad)/s]
したがって、振動の周期は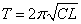 [s]である。
[s]である。
- よって、コンデンサのA極板の電荷Q[c]をあらわす式は、
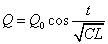 ・・・(4)
・・・(4)
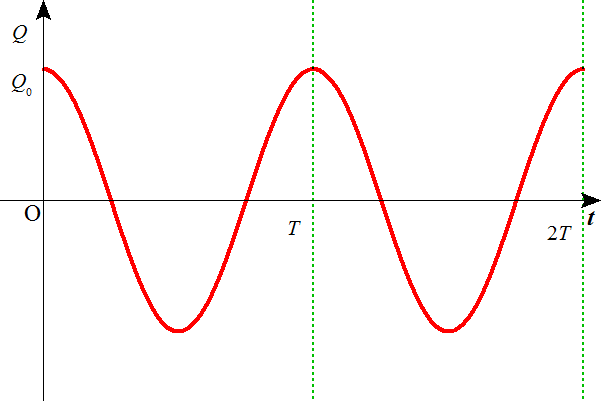
また、コイルをDからCに向かって流れる電流I[A]をあらわす式は、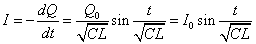 ・・・(5)
・・・(5)
ただし、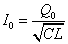
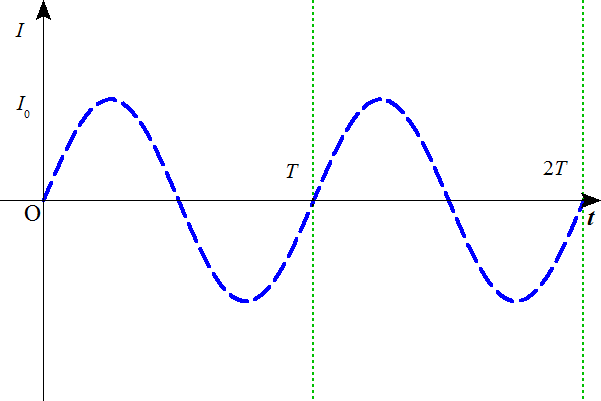
- 次に、コンデンサとコイルとのエネルギーのやり取りについて考える。
コンデンサに蓄えられる静電エネルギーUC[J]は、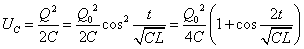
t=0のとき、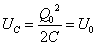 であるから、「エネルギー保存則」より、コイルが蓄えるエネルギーUL[J]は、
であるから、「エネルギー保存則」より、コイルが蓄えるエネルギーUL[J]は、
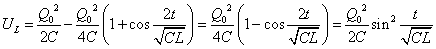
ここで、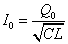 すなわち、
すなわち、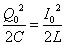 であるから、
であるから、
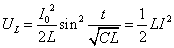
- コイルが蓄えるエネルギーUL[J]の式は、別の方法でも導ける。
[J=V・C=V・A・s]であるから、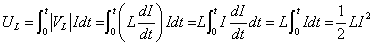
最後の変形は、「置換積分」0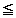 t
t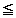 t→0
t→0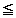 I
I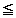 Iを用いている。
Iを用いている。
- 以上から、「LC振動回路」のエネルギー保存の式は、
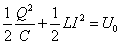 ・・・(6)
・・・(6)
- ここに抵抗を接続すると、コンデンサ、コイル間の電荷の移動のたびごとに「ジュール熱」が発生し、これによって全エネルギーが減少するから、振幅が次第に小さくなる「減衰振動」となるはずである。
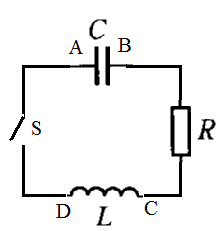
- キルヒホッフ第2法則は VC-VL-VR=0 と変わり、
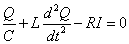
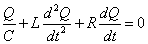
この微分方程式を解くのは、困難であるから、以下では、1周期の間は振幅の減衰が生じず、各周期の初めに不連続的に減衰が起こると仮定する。
- キルヒホッフ第2法則は VC-VL-VR=0 と変わり、
- 第n回めの振動の初めの電流Iの振幅がInであったとする。
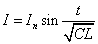 (n=0,1,2,・・・)
(n=0,1,2,・・・)
この1周期に抵抗Rで消費されるエネルギーUnは、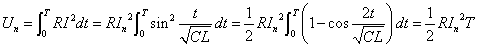 ・・・(7)
・・・(7)
ただし、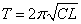
こうして、抵抗によるエネルギー消費を考慮すると、(5)式は、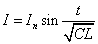
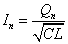 であるから、(4)式は、
であるから、(4)式は、
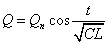
さらに、全エネルギーをあらわす(6)式は、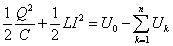
となる。 - では次に、Qn、Inについての「漸化式」を求めてみよう。
各周期のコンデンサ、コイルが蓄えるエネルギーの「最大値」はそれぞれ、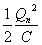
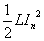
であるから、次の周期ではこれらがそれぞれ、Unだけ減少している。よって、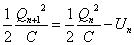 ・・・(8)
・・・(8)
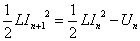 ・・・(9)
・・・(9)
(7)(8)より、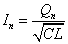 であるから、
であるから、
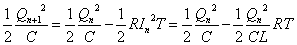
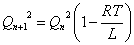
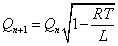
(7)(9)より、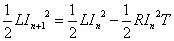
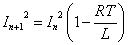
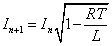
- このようにして、振幅が等比数列的に減少していく「減衰振動」であることが分かった。
ここでは、1周期の間は振幅が変わらず、周期の変わり目で「不連続的」に減衰が生じるかのように扱った。もちろん本当は、「連続的」に変化する筈だ。
「等比数列」を連続関数化すると、「指数関数」であることから、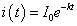
とおき、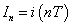 ,
, 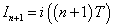
を満たすように定数kを定めよう。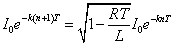
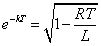
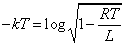
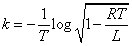
よって、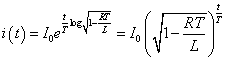
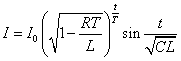
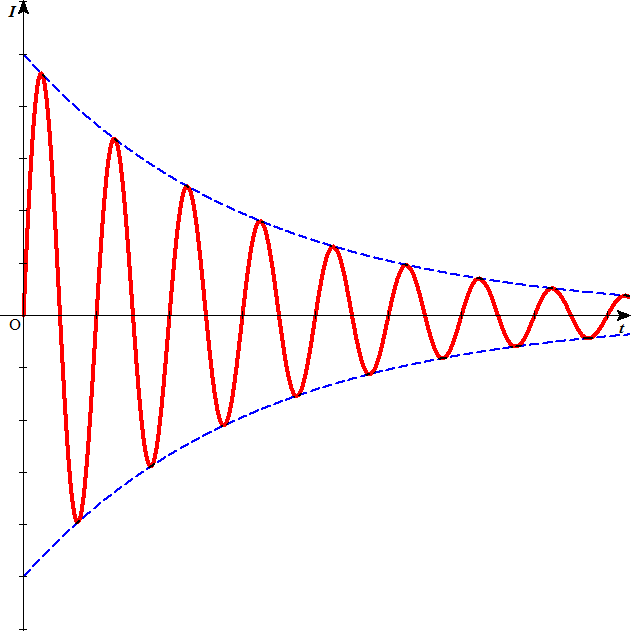
- このように、「減衰振動」とは、振幅が等比数列的に減少、すなわち、振動のグラフを包む線(「包絡線」という)が底が1より小さい指数関数であるような振動である。
- 【参考】この微分方程式(定数係数線形2階斉次微分方程式)を解いてみると・・・
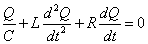 ・・・(*)
・・・(*)
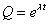 と、解の形を仮定する。
と、解の形を仮定する。
- 1階微分、2階微分して、
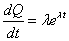
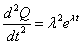
- (*)に代入すると、
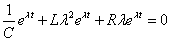
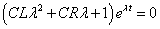
- eλt
 0だから、
0だから、
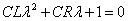
- 抵抗Rはそれほど大きくない、と思われるから、この2次方程式(特性方程式)の判別式は負になるとして、
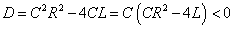
したがってλは次のような共役複素数解となる。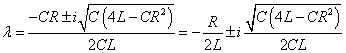
これらを、λ1 , λ2とおくことにする。 - ところで、複素変数では、指数関数と三角関数との間に次のような重要な関係があることが知られている。
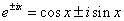
これは、以下の「マクローリン展開」を、それぞれ指数関数、三角関数に適用してみると、理解できる。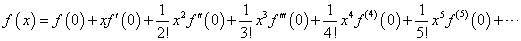
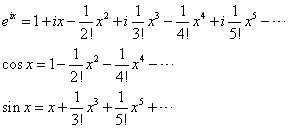
- したがって、
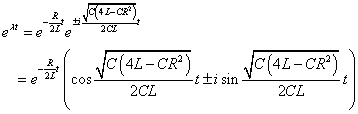
- eλ1t , eλ2tが(*)の解であるならば、それらを定数倍して「重ね合わせ」たものも解であることが知られている。
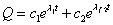
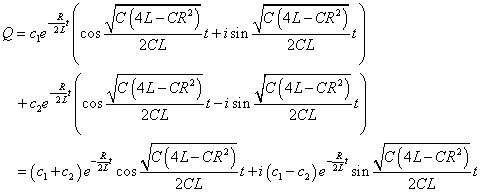
- c1+c1=Q0 , c1-c1=0となるように、虚数部がゼロになるように、選ぶこともできるから、
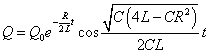
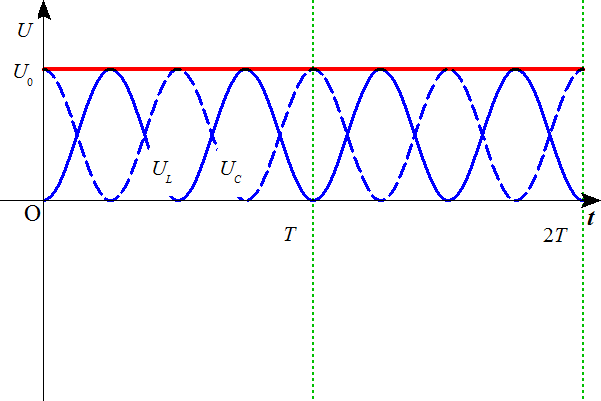
こうして、抵抗による減衰のある単振動の式が得られた。抵抗の影響によって、周期は少し小さい値になっているが、時間の経過とともに、振幅が次第に小さくなっても、一定の周期であることに注目。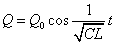
- 以下の図で破線は、抵抗による減衰のない場合、実線は、抵抗による減衰のある場合を示す。この図では周期の変化はほとんど検出できない。
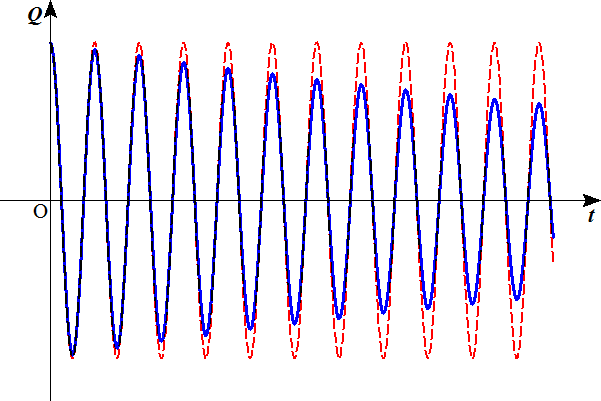
抵抗が小さい場合
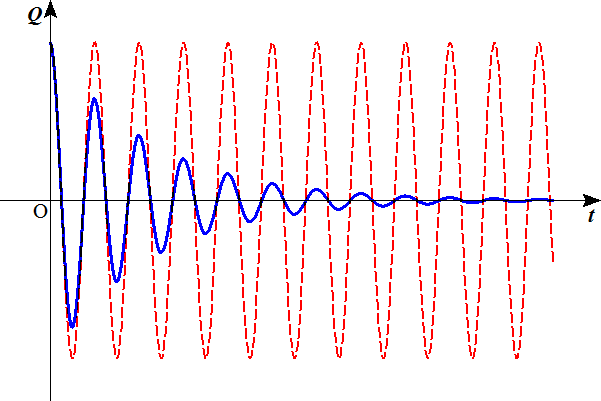
抵抗が大きい場合
- 下の図は交流発電機の概念図である。左から右に向かう磁場を横切って、長方形のコイルABCDが反時計回りに角速度ω[(rad)/s]で回転させる。ABの先には「整流子」(半回転ごとに接続先が逆転する仕組み)を介して抵抗に接続されている。
右図はこれを回転軸上手前から眺めたものである。平面ABCDの単位法ベクトルをn、これがx軸となす角をθとすれば、長方形ABCDをつらぬく磁束Φは、
Φ=B・nS=BScosθ=Babcosθ[wb]
とかける。時刻t=0にnがx軸方向、すなわち、長方形ABCDがy軸上にあったとすると、t秒後の磁束は、
Φ=Babcosωt[wb]
レンツの法則より、
ωBab=V0とおけば、抵抗の両端には、振幅V0でサインカーブを描いて時間的に変化する「交流」の起電力が得られることになる。
V=V0sinωt
- 交流電圧の実効値
上で得られた交流電源、
V=V0sinωt
について、1周期T=2π/ωについての平均をとると、
となり、0になってしまう。このようにプラスマイナスの間を変動する量は、そのまま平均をとっても、その実質的な「大きさ」を把握できないことが多い。このようなとき「2乗平均の平均値」という手法が、しばしば用いられる(「気体分子運動論」における「2乗平均速度」、統計学における「分散・標準偏差」の概念、など)。
こうして得られた電圧の2乗平均の正の平方根を、電圧の「実効値」と呼びVeと書く。
- 抵抗を流れる交流
交流電源の電圧を
[V]
とすると、「オームの法則」より、
[A]
電圧と時間の関係 電流と時間の関係
消費電力は、
[W=V・A=(J/c)・(c/s)=J/s]
1周期T=2π/ω[s]について、平均消費電力を求めると、
[W]
ここで、以下のようにして電圧、電流の「実効値」Ve,Ieを定めた。
実効値による表現
- コイルを流れる交流
交流電源の電圧を
[V]
コイルの両端に発生する「誘導起電力」は
[V]
「キルヒホッフ第2法則」より
V+V'=0
[V]
tで積分して、
(cは積分定数)
時刻t=0で最大の誘導電流(電源と逆向き)が流れるから、c=0
電圧と時間の関係 電流と時間の関係
消費電力は、
[W=V・A=(J/c)・(c/s)=J/s]
1周期T=2π/ω[s]について、平均消費電力を求めると、
[W]
実効値による表現
ここで、ωLは抵抗Rと同じ[Ω]の単位を持ち、電流の流れを妨げる役割を果たす。これを「誘導リアクタンス」と呼ぶ。
- コンデンサを流れる交流
交流電源の電圧を
[V]
この電圧によってコンデンサに蓄えられる電荷Q[c]は、
Q=CV=CV0sinωt
ここで、
[c=A・s]
だから、両辺をtで微分して、
I=ωCV0cosωt
電圧と時間の関係 電流と時間の関係
消費電力は、
[W=V・A=(J/c)・(c/s)=J/s]
1周期T=2π/ω[s]について、平均消費電力を求めると、
[W]
実効値による表現
Ie=ωCVe
ここで、は抵抗Rと同じ[Ω]の単位を持ち、電流の流れを妨げる役割を果たす。これを「容量リアクタンス」と呼ぶ。
- まとめ(抵抗・コイル・コンデンサの交流電源に対する応答)
[Ω] 電源電圧と電流の位相 平均消費電力 実効値 抵抗 R
(レジスタンス)同じ [W]
コイル ωL
(誘導リアクタンス)電流の位相が 遅れる
0[W] コンデンサ
(容量リアクタンス)電流の位相が 進む
0[W] Ie=ωCVe
- LCR直列回路
キルヒホッフ第2法則から、
ここで、直列であるから、コイル、コンデンサ、抵抗、交流電源を流れる電流はすべて等しいのでこれを、
I=I0sinωt
とおく。電源の位相はこれに対してずれるはずであるから、
V=V0sin(ωt+ψ)
とする。
ここでは右辺に「三角関数の合成」を用いている。あらためて、時間の基準の取り方を変え、電源電圧を
V=V0sinωt
これに対して電流の位相は電圧の位相に対して、ψ「遅れる」ことになるから、
I=I0sin(ωt-ψ)
とすれば、
ここで、Z(インピーダンス)[Ω]を次のように定義すれば、
電圧、電流のそれぞれの実効値について、Ve=IeZが成り立つことになる。一方、電流の位相の「遅れ角ψ」は次のように表される。
次に「共振周波数」について考える。
のとき、インピーダンスZ[Ω]は、最小となり、回路を流れる電流は最大となる。この状態を、「LCR回路が交流電源と共振した」といい、そのときの交流電源の周波数を「共振周波数」と呼ぶ。
,
- 変圧器の原理
,
左側の回路(1次コイル)に交流電流を流すと、「相互誘導」により、右側の回路(2次コイル)のコイルの両端に誘導起電力が発生する。
1次コイルにかかる電圧を、V1sinωtとすると、1次コイルを流れる電流I1は、
これによって、2次コイルの両端には、次のような誘導起電力が発生する。
自己インダクタンス、相互インダクタンスについての詳細は上の「相互誘導」参照
コイルの巻き数などを調整することで、1次側の電圧と異なる電圧の交流を2次側から取り出すことができる。
|
「電流」と「磁場」との相互関係の、3つの側面
【参考】マックスウェルの電磁気学の体系
|